- 2021-06-22 发布 |
- 37.5 KB |
- 12页

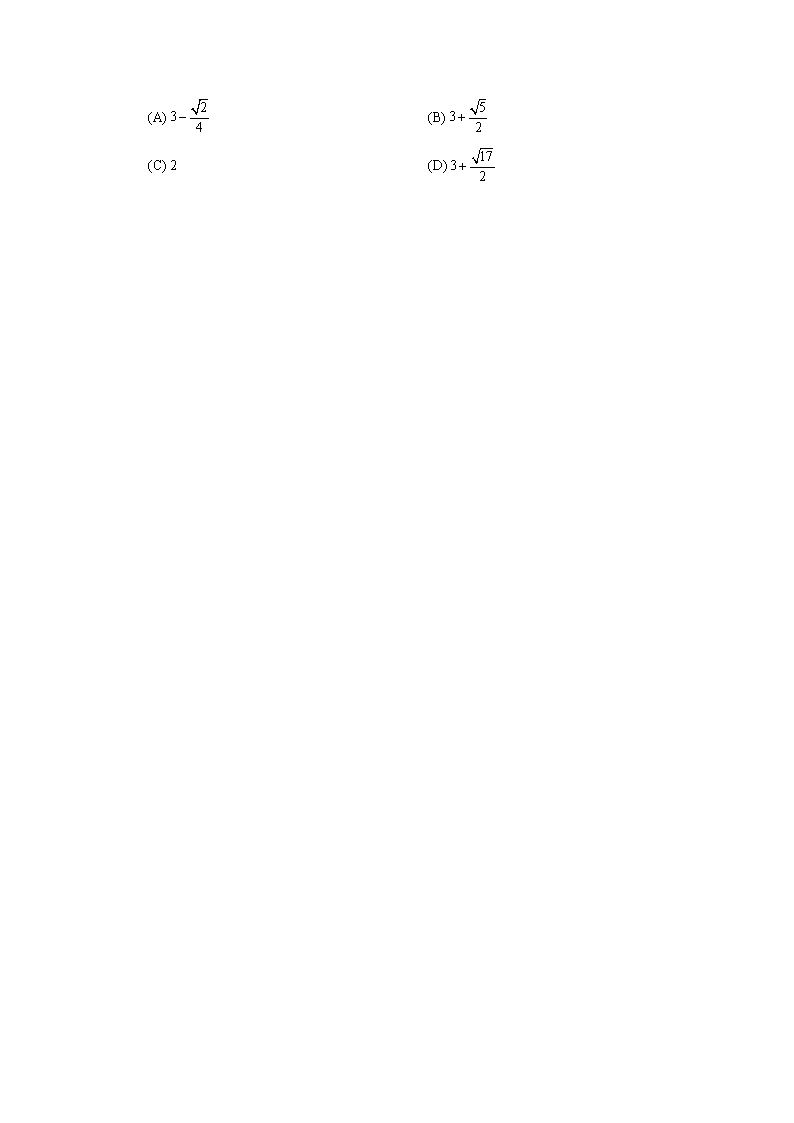
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2017届四川省资阳市高三4月模拟考试(2017
资阳市高中2014级高考模拟考试 数 学(文史类) 第Ⅰ卷 (选择题 共60分) 一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1.设全集U=R,集合,则图中阴影部分所表示的集合为 (A)或 (B)或 (C) (D) 2.已知等差数列中,,则,则数列的公差为 (A) 2 (B) 3 (C) 4 (D) 5 3.在集合中随机取一个实数m,若的概率为,则实数a的值为 (A) 5 (B) 6 (C) 9 (D) 12 4.一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为 (A) (B) (C) (D) 5.双曲线E:(,)的一个焦点F到E的渐近线的距离为,则E 的离心率是 (A) (B) (C) 2 (D) 3 6.定义在上的函数满足则 (A) 3 (B) 2 (C) (D) 7.已知MOD函数是一个求余函数,记表示m除以n的余数,例如.右图是某个算法的程序框图,若输入m的值为48时,则输出的值为 (A) 7 (B) 8 (C) 9 (D) 10 8.已知函数(其中)图象的一条对称轴方程为,则的最小值为 (A) 2 (B) 4 (C) 10 (D) 16 9.已知,,下列不等式成立的是 (A) (B) (C) (D) 10.对于两条不同的直线m,n和两个不同的平面,以下结论正确的是 (A) 若,∥,m,n是异面直线,则相交 (B) 若,,∥,则∥ (C) 若,∥,m,n共面于β,则m∥n (D) 若,n⊥β,α,β不平行,则m,n为异面直线 11.抛物线的焦点为F,点,为抛物线上一点,且不在直线上,则周长的最小值为 (A) 10 (B) 11 (C) 12 (D) 12.如图,在直角梯形中,,∥,,,图中圆弧所在圆的圆心为点C,半径为,且点P在图中阴影部分(包括边界)运动.若,其中,则的最大值为 (A) (B) (C) 2 (D) 第Ⅱ卷(非选择题 共90分) 本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须做答。第22题、第23题为选考题,考生根据要求做答。 注意事项: 必须使用0.5毫米黑色墨迹签字笔在答题卡上题目指示的答题区域内作答。作图时可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚。答在试题卷、草稿纸上无效。 二、填空题:本大题共4小题,每小题5分,共20分。 13.已知i是虚数单位,复数z满足,则_____. x 30 40 50 60 y 25 30 40 45 14.某厂在生产某产品的过程中,产量(吨)与生产能耗(吨)的对应数据如右表所示.根据最小二乘法求得回归直线方程为.当产量为80吨时,预计需要生产能耗为 吨. 15.设命题:函数的定义域为R;命题:当时,恒成立,如果命题“p∧q”为真命题,则实数的取值范围是 . 16.我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为_______日. (结果保留一位小数,参考数据:,) 三、解答题:解答应写出文字说明、证明过程或演算步骤。 17.(本小题满分12分) 在中,内角A,B,C的对边分别为a,b,c,已知. (Ⅰ) 求角A的大小; (Ⅱ) 若,的面积为,求的值. 18.(本小题满分12分) 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行” 的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图. (Ⅰ) 求图中的值; (Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取2人进行座谈,求所抽取的两人中至少有一名女生的概率. 19.(本小题满分12分) 如图,在三棱柱中,底面△ABC是等边三角形,且平面ABC,为的中点. (Ⅰ) 求证:直线∥平面A1CD; (Ⅱ) 若,E是的中点,求三棱锥的体积. 20.(本小题满分12分) 如图,在平面直角坐标系中,椭圆W:的离心率为,直线l:y=2上的点和椭圆W上的点的距离的最小值为1. (Ⅰ) 求椭圆W的方程; (Ⅱ) 已知椭圆W的上顶点为A,点B,C是W上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线与的斜率分别为,. ① 求证:为定值; ② 求△CEF的面积的最小值. 21.(本小题满分12分) 已知函数,其中. (Ⅰ) 当a=-1时,求证:; (Ⅱ) 对任意,存在,使成立,求a的取值范围. (其中e是自然对数的底数,e=2.71828…) 请考生在22,23题中任选一题做答,如果多做,则按所做的第一题计分,做答时,请用2B铅笔在答题卡上将所选题目题号的方框涂黑。 22. (本小题满分10分) 选修4-4:坐标系与参数方程 已知在平面直角坐标系中,曲线的参数方程是(为参数),以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程是. (Ⅰ) 求曲线与交点的平面直角坐标; (Ⅱ) 点分别在曲线,上,当最大时,求的面积(为坐标原点). 23.(本小题满分10分) 选修4-5:不等式选讲 已知函数. (Ⅰ) 解不等式; (Ⅱ) 若,,求证:. 资阳市高中2014级高考模拟考试 数学参考答案及评分意见(文史类) 一、选择题:本大题共12小题,每小题5分,共60分。 1.D 2.A 3.B 4.C 5.C 6.A 7.C 8.B 9.D 10.C 11.B 12.B 二、填空题:本大题共5小题,每小题4分,共20分。 13. ;14. 59.5;15.;16. 2.6. 三、解答题:本大题共70分。 17.(本小题满分12分) (Ⅰ)由已知得, 2分 化简得, 整理得,即, 4分 由于,则,所以. 6分 (Ⅱ)因为,所以. 8分 根据余弦定理得, 10分 即,所以b+c=3. 12分 18.(本小题满分12分) (Ⅰ)由,解得. 4分 (Ⅱ)满意度评分值在[90,100]内有人, 其中女生2人,男生4人. 5分 设其中女生为,男生为,从中任取两人,所有的基本事件为(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4),(b1,b2),(b1,b3),(b1,b4),(b2,b3),(b2,b4),(b3,b4)共15个,至少有1人年龄在[20,30)内的有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4)共9个. 所以,抽取的两人中至少有一名女生的概率为,即为. 12分 19.(本小题满分12分) (Ⅰ)连接AC1,交A1C于点F, 则F为AC1的中点,又为的中点, 所以∥DF, 又平面A1CD,又平面A1CD, 所以∥平面A1CD. 5分 (Ⅱ)三棱锥的体积 . 7分 其中三棱锥的高h等于点C到平面ABB1A1的距离,可知. 9分 又. 所以. 12分 20.(本小题满分12分) (Ⅰ)由题知,由, 所以. 故椭圆的方程为. 3分 (Ⅱ)① 证法一:设,则, 因为点B,C关于原点对称,则, 所以. 6分 证法二:直线AC的方程为, 由得, 解得,同理, 因为B,O,C三点共线,则由, 整理得, 所以. 6分 ②直线AC的方程为,直线AB的方程为,不妨设,则, 令y=2,得, 而, 所以,△CEF的面积 . 8分 由得, 则,当且仅当取得等号, 所以△CEF的面积的最小值为. 12分 21.(本小题满分12分) (Ⅰ)当a=-1时,(x>0), 则,令,得. 当时,,单调递增;当时,,单调递减. 故当时,函数取得极大值,也为最大值,所以, 所以,,得证. 4分 (II)原题即对任意,存在,使成立, 只需. 5分 设,则, 令,则对于恒成立, 所以为上的增函数, 于是,即对于恒成立, 所以为上的增函数,则. 8分 令,则, 当a≥0时,为的减函数,且其值域为R,符合题意. 当a<0时,,由得, 由得,则p(x)在上为增函数;由得,则p(x)在上为减函数,所以, 从而由,解得. 综上所述,a的取值范围是. 12分 22. (本小题满分10分) 选修4-4:坐标系与参数方程 (Ⅰ)由得 则曲线的普通方程为. 又由,得,得. 把两式作差得,,代入, 可得交点坐标为为. 5分 (Ⅱ) 由平面几何知识可知, 当依次排列且共线时,最大,此时, 直线的方程为,则到的距离为, 所以的面积为. 10分 23.(本小题满分10分) 选修4-5:不等式选讲 (Ⅰ)原不等式即为. 当时,则,解得; 当时,则,此时不成立; 当时,则,解得. 所以原不等式的解集为或. 5分 (Ⅱ)要证,即,只需证明. 则有 . 因为,, 则, 所以,原不等式得证. 10分查看更多