数学（文）卷·2018届河南省林州市第一中学高二4月调研考试（2017-04）

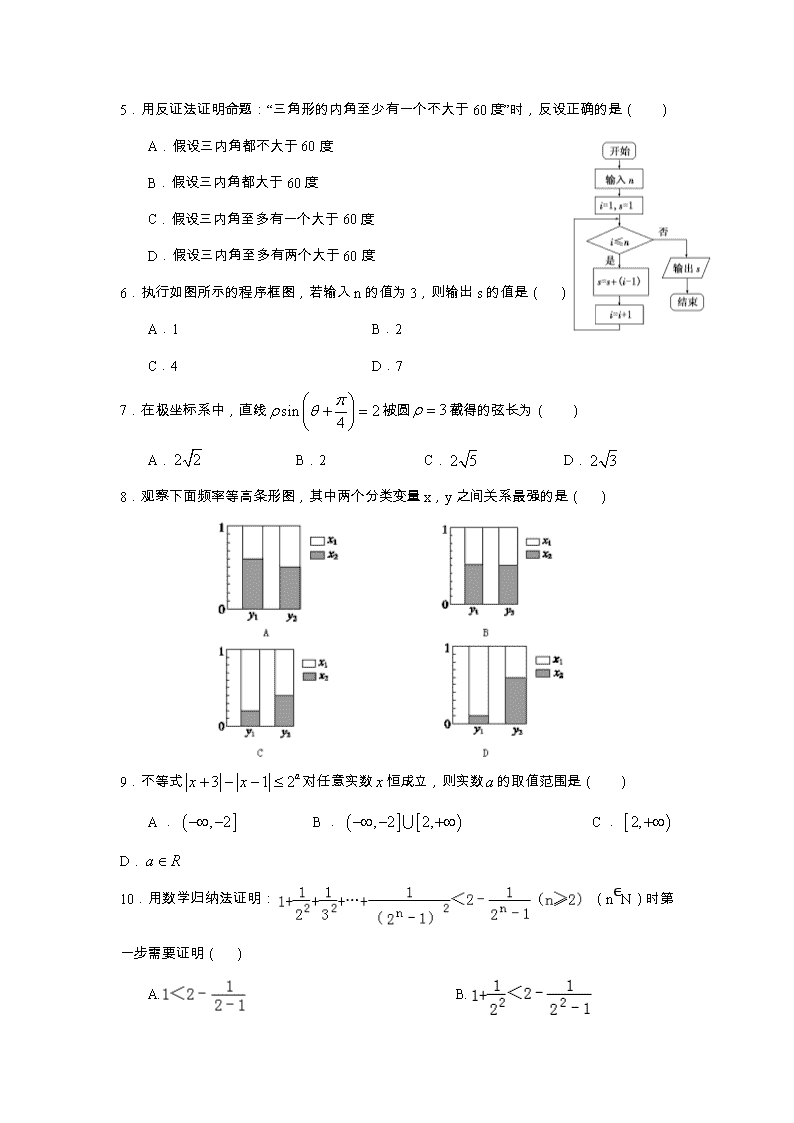
数学（文）卷·2018届河南省林州市第一中学高二4月调研考试（2017-04）

‎2015级高二下学期4月调研考试 数学（文）试题 一、选择题（共60分）‎ ‎1.若＝1－i，则复数z的共轭复数为（ ）‎ A．0 B．1 C．2 D．－2‎ ‎2．下列使用类比推理所得结论正确的是（ ）‎ A．直线，若，则．类推出：向量，若，则 B．同一平面内，直线，若，则．类推出：空间中，直线，若，则． ‎ C．实数，若方程有实根，则．类推出：复数，若方程有实数根，则．‎ D．以点为圆心，为半径的圆的方程是．类推出：以点为球心，为半径的球的方程是 ‎3．对于a，b∈（0，＋∞），a＋b≥2（大前提）， （小前提），所以（结论）。以上推理过程中的错误为（） ‎ A．大前提 B．小前提 C．结论 D．无错误 ‎4.某医疗所为了检查新开发的流感疫苗对甲型H1N1流感的预防作用，把1000名注射疫苗的人与另外1000名未注射疫苗的人半年的感冒记录比较，提出假设“这种疫苗不能起到预防甲型H1N1流感的作用”，并计算，则下列说法正确的是（ ）‎ A．这种疫苗能起到预防甲型H1N1流感的有效率为1%‎ B．若某人未使用疫苗则他在半年中有99%的可能性得甲型H1N1‎ C．有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”‎ D．有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”‎ ‎5．用反证法证明命题：“三角形的内角至少有一个不大于60度”时，反设正确的是（ ）‎ A．假设三内角都不大于60度 ‎ B．假设三内角都大于60度 C．假设三内角至多有一个大于60度 ‎ D．假设三内角至多有两个大于60度 ‎6．执行如图所示的程序框图，若输入n的值为3，则输出s的值是（ ）‎ A．1 B．2 ‎ C．4 D．7‎ ‎7．在极坐标系中，直线被圆截得的弦长为（ ）‎ A． B．2 C． D．‎ ‎8．观察下面频率等高条形图，其中两个分类变量x，y之间关系最强的是（ ）‎ ‎9．不等式对任意实数恒成立，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎10．用数学归纳法证明：（n∈N）时第一步需要证明（ ）‎ A. B.‎ C. D.‎ ‎11．已知a，b，c∈（0，1），则对于（1﹣a）b，（1﹣b）c，（1﹣c）a说法正确的是（ ）‎ A.不能都大于 B.都大于 C.都小于 D.至少有一个大于 ‎12.如图所示，面积为S的平面凸四边形的第条边的边长记为，此四边形内任一点到第条边的距离记为，若，则．类比以上性质，体积为V的三棱锥的第个面的面积记为，此三棱锥内任一点到第个面的距离记为，若，则（ ）‎ A． B． C． D．‎ 二、填空题（共20分）‎ ‎13．某单位为了了解用电量（千瓦时）与气温（℃）之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：‎ 气温/℃‎ ‎18‎ ‎13‎ ‎10‎ ‎-1‎ 用电量/千瓦时 ‎24‎ ‎34‎ ‎38‎ ‎64‎ 由表中数据得到线性回归方程中，预测当气温为-4℃时，用电量的度数约为 ．‎ ‎14. 已知>0，>0，且，若恒成立，则实数的取值范围是 ．‎ ‎15. 不等式对满足的一切实数恒成立，则 的取值范围是_________.‎ ‎16．观察下列等式 ‎1=1‎ ‎2+3+4=9‎ ‎3+4+5+6+7=25‎ ‎4+5+6+7+8+9+10=49‎ ‎……‎ 照此规律，第个等式为 。‎ 三、解答题（共70分）‎ ‎17. (10分)已知关于x的方程：x2﹣（6+i）x+9+ai=0（a∈R）有实数根b．‎ ‎（1）求实数a，b的值．‎ ‎（2）若复数z满足|﹣a﹣bi|﹣2|z|=0，求z为何值时，|z|有最小值，并求出|z|的值．‎ ‎18. （12分）．“奶茶妹妹”对某段时间的奶茶销售量及其价格进行调查，统计出售价元和销售量杯之间的一组数据如下表所示：‎ 价格 ‎5‎ ‎5.5‎ ‎6.5‎ ‎7‎ 销售量 ‎12‎ ‎10‎ ‎6‎ ‎4‎ 通过分析，发现销售量对奶茶的价格具有线性相关关系．‎ ‎（1）求销售量对奶茶的价格的回归直线方程；‎ ‎（2）欲使销售量为13杯，则价格应定为多少？‎ 注：在回归直线中，．‎ ‎19. （12分）2016年夏季奥运会将在巴西里约热内卢举行，体育频道为了解某地区关于 奥运会直播的收视情况，随机抽取了名观众进行调查，其中岁以上的观众有 名，下面是根据调查结果绘制的观众准备平均每天收看奥运会直播时间的频率分布表(时间：分钟)：‎ 分组 频率 将每天准备收看奥运会直播的时间不低于分钟的观众称为“奥运迷”，已知“奥运迷”中有名岁以上的观众.‎ ‎（1）根据已知条件完成下面的列联表，并据此资料你是否有以上的把握认为“奥运迷”与年龄有关？‎ 非“奥运迷”‎ ‎“奥运迷”‎ 合计 岁以下 岁以上 合计 ‎（2）将每天准备收看奥运会直播不低于分钟的观众称为“超级奥运迷”，已知“超级奥运迷”中有名岁以上的观众，若从“超级奥运迷”中任意选取人，求至少有名岁以上的观众的概率.‎ 附：‎ ‎20.（12分）． 已知函数．‎ ‎（1）解不等式；‎ ‎（2）若存在实数使得，求实数的取值范围 ‎21.（12分）．在平面直角坐标系中，曲线的参数方程为（ 为参数），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，得曲线的极坐标方程为 ‎（） ‎ ‎（Ⅰ）求曲线的普通方程和曲线的直角坐标方程；‎ ‎（Ⅱ）直线： （为参数）过曲线与轴负半轴的交点，求与直线平行且与曲线相切的直线方程 ‎ ‎22.（12分）．设数列的前n项的和与的关系是.‎ ‎（1）求并归纳出数列的通项（不需证明）；‎ ‎（2）求数列的前项和.‎ ‎2015级高二下学期4月调研考试 数学（文）答案 ‎1．C 2.D 3.B 4.C 5.B 6.C 7.C 8.D 9.C 10.C 11.A 12.D 13. ‎ 14..‎ ‎15. 16．‎ ‎17.（1）∵b是方程x2﹣（6+i）x+9+ai=0（a∈R）的实根，‎ ‎∴（b2﹣6b+9）+（a﹣b）i=0，∴解之得a=b=3．‎ ‎（2）设z=x+yi（x，y∈R），由|﹣3﹣3i|=2|z|，‎ 得（x﹣3）2+（y+3）2=4（x2+y2），即（x+1）2+（y﹣1）2=8，‎ ‎∴z点的轨迹是以O1（﹣1，1）为圆心，2为半径的圆，如图所示，‎ 如图，当z点在OO1的连线上时，|z|有最大值或最小值，‎ ‎∵|OO1|=半径r=2，∴当z=1﹣i时.|z|有最小值且|z|min=．‎ ‎18．（1）；（2）.‎ ‎（1）， ，故回归直线方程为.‎ ‎（2）令解得 答：商品的价格定为4.75元 ‎19.（1）由频率分布表可知，在轴取的人中，“奥运迷”有人，从完成列联表如下：‎ 非“奥运迷”‎ ‎“奥运迷”‎ 合计 岁以下 岁以上 合计 ‎.‎ 因为，所以没有以上的把握认为“奥运迷”与年龄有关.‎ ‎（2）由频率分布表可知，“超级奥运迷”有人，从而所有可能结果所组成的基本事件空间为：‎ 其中表示男性，表示女性，. 由个基本事件组成，且是等可能的，用表示事件“任意选人，至少有 名岁以上观众”，则，即事件包含个基本事件，所以.‎ ‎20．（1）； （2）.‎ ‎（1） 或或 解得或，解集为 ‎（2），‎ ‎，所以只需满足 ‎21. 试题解析：（Ⅰ）曲线的普通方程为： ‎ 由得，‎ ‎∴曲线的直角坐标方程为： ‎ ‎（或：曲线的直角坐标方程为： ）‎ ‎（Ⅱ）曲线：与轴负半轴的交点坐标为，‎ 又直线的参数方程为：，∴ ，得，[来源]‎ 即直线的参数方程为： 得直线的普通方程为：，‎ 设与直线平行且与曲线相切的直线方程为：‎ ‎∵曲线是圆心为，半径为5的圆，得，解得或 故所求切线方程为：或 ‎ ‎22. 试题解析：（1）：，所以.‎ (2) 由（1）得所以，‎ 由错位相消法得