2021届课标版高考理科数学大一轮复习课件：1-1　集合的概念及运算（讲解部分）

2021届课标版高考理科数学大一轮复习课件：1-1　集合的概念及运算（讲解部分）

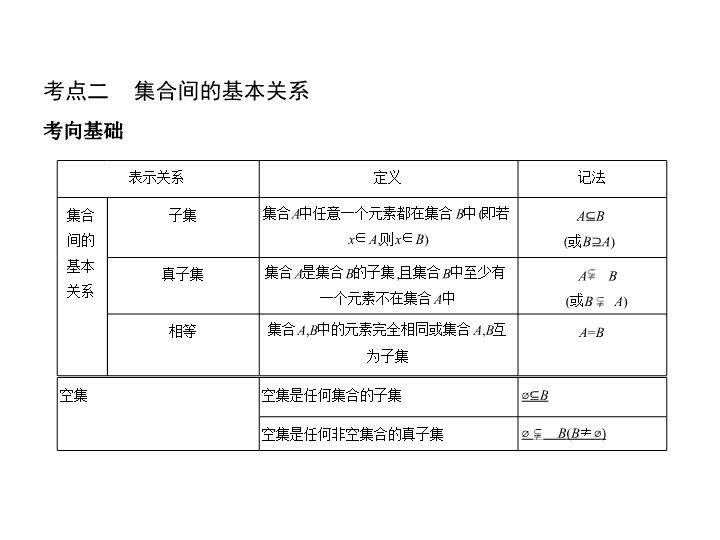
考点一    集合的含义与表示 考点清单 考向基础 1.集合中元素的三个特性:确定性、 互异性 、无序性. 2.集合中元素与集合的关系有且仅有两种: 属于 (用符号“∈”表示)和 不 属于 (用符号“ ∉ ”表示). 名称 非负整数集 (自然数集) 正整数集 整数集 有理数集 实数集 符号 N N * 或N + Z Q R 3.常用数集及其符号表示 注意 　集合元素互异性的应用:(1)利用集合元素的互异性找到解题的切入 点;(2)在解答完毕时,注意检查集合的元素是否满足互异性,以确保答案正确. 考向突破 考向    确定集合中元素的个数 例     (2019宁夏银川4月模拟,2)已知集合 A ={1,2,3},集合 B ={ z | z = x - y , x ∈ A , y ∈ A },则集合 B 中元素的个数为   (　　) A.4　　　　    B.5　　　　    C.6　　　　    D.7 解析 　∵ A ={1,2,3}, B ={ z | z = x - y , x ∈ A , y ∈ A }, ∴ x =1,2,3, y =1,2,3. 当 x =1时, x - y =0,-1,-2; 当 x =2时, x - y =1,0,-1; 当 x =3时, x - y =2,1,0. 即 x - y =-2,-1,0,1,2,即 B ={-2,-1,0,1,2}.共有5个元素.故选B. 答案     B 考点二    集合间的基本关系 考向基础 表示关系 定义 记法 集合 间的 基本 关系 子集 集合 A 中任意一个元素都在集合 B 中(即若 x ∈ A ,则 x ∈ B ) A ⊆ B (或 B ⊇ A ) 真子集 集合 A 是集合 B 的子集,且集合 B 中至少有一个元素不在集合 A 中 A B (或 B A ) 相等 集合 A , B 中的元素完全相同或集合 A , B 互为子集 A = B 空集 空集是任何集合的子集 ⌀⊆ B 空集是任何非空集合的真子集 ⌀ B ( B ≠ ⌀ ) 注意　 在涉及集合之间的关系时,若未指明集合非空,则要考虑空集的可能 性,如:若 A ⊆ B ,则要考虑 A = ⌀ 和 A ≠ ⌀ 两种可能. 若 A 为有限集合,card( A )= n ( n ∈N * ),则: A 的子集个数是2 n ; A 的真子集个数是2 n -1; A 的非空子集个数是2 n -1; A 的非空真子集个数是2 n -2. 考向突破 考向    集合间基本关系的判断 例     (2018山东沂水第一中学第三轮考试,2)设全集 U =R,则集合 M ={0,1,2} 和 N ={ x | x ·( x -2)·log 2 x =0}的关系用韦恩图表示正确的是   (　　)   解析      N ={ x | x ·( x -2)·log 2 x =0}={1,2},∵ M ={0,1,2},∴ N 是 M 的真子集,故选A. 答案     A 考点三    集合的基本运算 考向基础 集合的并集 集合的交集 集合的补集 符号 表示 A ∪ B A ∩ B 若全集为 U ,则集合 A 的 补集为 ∁ U A 图形 表示       意义 { x | x ∈ A 或 x ∈ B } { x | x ∈ A ,且 x ∈ B } { x | x ∈ U ,且 x ∉ A } 性质 A ∪ ⌀ = A ; A ∪ A = A ; A ∪ B = B ∪ A ; A ∪ B = A ⇔ B ⊆ A A ∩ ⌀ = ⌀ ; A ∩ A = A ; A ∩ B = B ∩ A ; A ∩ B = A ⇔ A ⊆ B A ∪ ( ∁ U A )= U ; A ∩ ( ∁ U A )= ⌀ ; ∁ U ( ∁ U A )= A ; ∁ U ( A ∪ B )=( ∁ U A ) ∩ ( ∁ U B ); ∁ U ( A ∩ B )=( ∁ U A ) ∪ ( ∁ U B ) 考向突破 考向    集合的运算 例　 (1)(2020届河南百校联盟高三尖子生开学联考,1)设集合 A ={ x ∈N|( x - 3)( x +2) ≤ 0}, B ={ y | y >2},则 A ∩ ( ∁ R B )=   (　　) A.{0,1,2}　　　　    B.{0,1} C.{-2,-1,0,1,2}　　　　    D.{-2,-1,0,1} (2)(2019江西九江二模,2)已知全集 U =R,集合 A ={ x | x -4 ≤ 0}, B ={ x |ln x <2},则 ∁ U ( A ∩ B )=   (　　) A.{ x | x >4}　　　　    B.{ x | x ≤ 0或 x >4} C.{ x |0< x ≤ 4}　　　　    D.{ x | x <4或 x ≥ e 2 } 解析　 (1)依题意得 A ={ x ∈N|( x -3)( x +2) ≤ 0}={0,1,2,3}, ∁ R B ={ y | y ≤ 2},故 A ∩ ( ∁ R B )={0,1,2}. (2)集合 A ={ x | x -4 ≤ 0}={ x | x ≤ 4}, B ={ x |ln x <2}={ x |0< x 4},故选B. 答案 　(1)A　(2)B 方法1     解决集合间基本关系问题的方法 1.判断集合之间关系的方法 (1)化简集合,从表达式中寻找两集合间的关系. (2)用列举法表示集合,从元素中寻找关系. (3)利用数轴,在数轴上表示出两个集合(集合为数集),比较区间之间的包含 关系,从而确定集合与集合的关系. 2.根据两个集合之间的关系确定参数的取值范围 已知两个集合间的关系求参数的关键是将两集合间的关系转化为元素间 的关系,进而转化为参数满足的关系.解决这类问题常常需要合理利用数 轴、Venn图帮助分析. 方法技巧 例1　 (1)(2019湖北天门调研,1)集合 M =   , N =   ,则   (　　) A. M = N 　　　　    B. M N C. N M 　　　　    D. M 与 N 没有相同的元素 (2)(2018山东济南期末,2)已知集合 A ={ x | ax -6=0}, B ={ x ∈N|1 ≤ log 2 x <2},且 A ∪ B = B ,则实数 a 的所有值构成的集合是   (　　) A.{2}　　　　    B.{3}　　　　     C.{2,3}　　　　    D.{0,2,3} 对于涉及 A ∪ B=A 或 A ∩ B=A 的问题 , 可利用集合的运算性质 , 转化为相关集合之间的关系求解 , 注意空集的特殊性 . 解题导引 (1)   (2)   解析 　(1)由题可知集合 M =   =   x   x =   (2 k +1), k ∈Z   , N =   =   x   x =   ·( k +2), k ∈Z   ,当 k ∈Z时,2 k +1是奇数, k +2是整 数,又知奇数均为整数,而整数不一定为奇数,所以 M N ,故选B. (2) B ={ x ∈N|1 ≤ log 2 x <2}={2,3}.因为 A ∪ B = B ,所以 A ⊆ B .当 A = ⌀ 时,显然 a = 0,符合题意.当 A ≠ ⌀ 时,得 a ≠ 0,此时 A ={ x | ax -6=0}=   ,由题意可得   =2或   =3,解得 a =3或 a =2,所以实数 a 的所有值构成的集合为{0,2,3}.故选D. 答案 　(1)B　(2)D 方法2      集合运算问题的求解方法 集合的基本运算包括集合间的交、并、补运算,解决此类问题应注意以下 几点:一是看集合的组成元素,这是解决问题的前提;二是把集合化简,先化 简再研究其关系并进行运算;三是注意数形结合思想的应用,在进行集合运 算时要尽可能地借助Venn图或数轴使抽象问题直观化.一般地,集合元素 离散时用Venn图表示;集合元素连续时用数轴表示,用数轴表示时注意端 点值的取舍. 例2　 (1)(2019河北唐山一中期中,1)已知集合 A ={ x |log 2 x <1}, B ={ x | x 2 + x -2< 0},则 A ∩ B =   (　　) A.(- ∞ ,2)　　　　    B.(0,1)　　　　     C.(0,2)　　　　    D.(-2,1) (2)(2018河北衡水中学、河南郑州一中3月联考,1)已知全集 U ={1,2,3,4,5,6, 7,8}, A ={3,4,5}, B ={1,3,6},则集合{2,7,8}是   (　　) A. A ∪ B 　　　　    B. A ∩ B 　　　　     C. ∁ U ( A ∩ B )　　　　    D. ∁ U ( A ∪ B ) 解析 　(1)由log 2 x <1=log 2 2,解得0< x <2,即 A =(0,2),由 x 2 + x -2<0得( x -1)( x +2)<0, 解得-2< x <1,即 B =(-2,1),借助数轴,可得 A ∩ B =(0,1),故选B.   (2)解法一:由题意可知 ∁ U A ={1,2,6,7,8}, ∁ U B ={2,4,5,7,8},∴( ∁ U A ) ∩ ( ∁ U B ) ={2,7,8}.由集合的运算性质可知( ∁ U A ) ∩ ( ∁ U B )= ∁ U ( A ∪ B ),即 ∁ U ( A ∪ B )= {2,7,8},故选D. 解法二:画出韦恩图(如图所示),由图可知 ∁ U ( A ∪ B )={2,7,8}.故选D.   答案 　(1)B　(2)D