- 2021-06-21 发布 |
- 37.5 KB |
- 15页

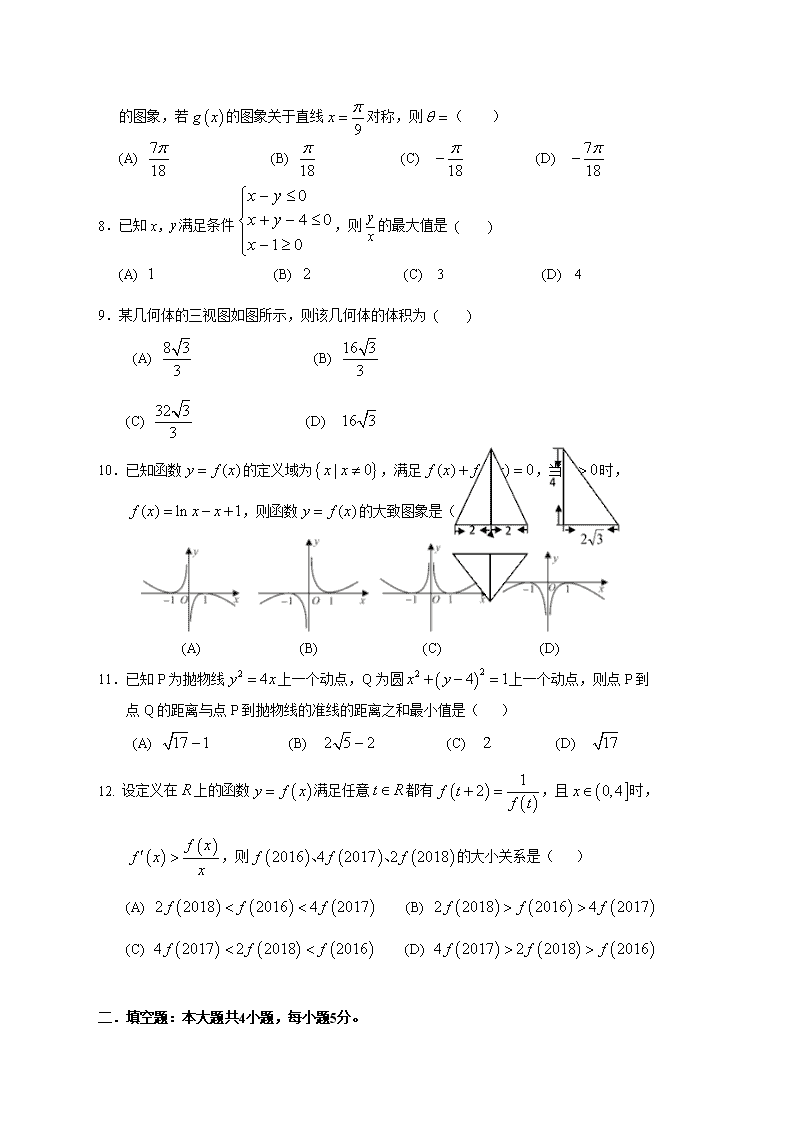

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届广东省惠州一中(惠州市)高三第三次调研考试(2018
惠州市 2018 届高三第三次调研考试 文科数学 全卷满分 150 分,时间 120 分钟. 一.选择题:本大题共 12 小题,每小题 5 分。在每个小题给出的四个选项中,只有一项是符合题 目要求的。 1. 集合 , ,则 = ( ) (A) (B) (C) (D) 2.设 ( 为虚数单位),则 ( ) (A) (B) (C) (D) 2 3.等比数列 中, , ,则 ( ) (A) 8 (B) 16 (C) 32 (D) 64 4. 已知向量 , 则 ( ) (A) (B) (C) (D) 5.下列说法中正确的是( ) (A) “ ”是“函数 是奇函数”的充要条件 (B) 若 ,则 (C) 若 为假命题,则 均为假命题 (D) “若 ,则 ”的否命题是“若 ,则 ” 6.已知输入实数 ,执行如图所示的流程图,则输出的 是 ( ) (A) (B) (C) (D) 7.将函数 ( )的图象向右平移 个单位后得到函数 }{ 022 ≤−−= xxxA }{ 1<= xxB )( BCA R }{ 1x x > }{ 1 2x x< ≤ }{ 1x x ≥ }{ 1 2x x≤ ≤ 1 iz i = − i 1 z = 2 2 2 1 2 { }na 1 2 2a a+ = 4 5 4a a+ = 10 11a a+ = a b⊥ 2,a b= = 2a b− = 2 2 2 2 5 10 (0) 0f = ( )f x 2 0 0 0: , 1 0p x R x x∃ ∈ − − > 2: , 1 0p x R x x¬ ∀ ∈ − − < p q∧ ,p q 6 πα = 1sin 2 α = 6 πα ≠ 1sin 2 α ≠ 12x = x 25 102 103 51 ( ) ( )1 cos 24f x x θ= + 2 πθ < 5 12 π ( )g x 开始 输 入 x n=1 n≤3 输 出 x 否 结束 x=2x+1n=n+1 是 的图象,若 的图象关于直线 对称,则 ( ) (A) (B) (C) (D) 8.已知 , 满足条件 ,则 的最大值是 ( ) (A) (B) (C) 3 (D) 4 9.某几何体的三视图如图所示,则该几何体的体积为 ( ) (A) (B) (C) (D) 10.已知函数 的定义域为 ,满足 ,当 时, ,则函数 的大致图象是( ) (A) (B) (C) (D) 11.已知 P 为抛物线 上一个动点,Q 为圆 上一个动点,则点 P 到 点 Q 的距离与点 P 到抛物线的准线的距离之和最小值是( ) (A) (B) (C) (D) 12. 设定义在 上的函数 满足任意 都有 ,且 时, ,则 的大小关系是( ) (A) (B) (C) (D) 二.填空题:本大题共4小题,每小题5分。 2 4y x= ( )22 4 1x y+ − = 17 ( )g x 9x π= θ = 7 18 π 18 π 18 π− 7 18 π− x y 0 4 0 1 0 x y x y x − ≤ + − ≤ − ≥ y x 1 2 8 3 3 16 3 3 32 3 3 16 3 ( )y f x= { }| 0x x ≠ ( ) ( ) 0f x f x+ − = 0x > ( ) ln 1f x x x= − + ( )y f x= 17 1− 2 5 2− 2 R ( )y f x= t R∈ ( ) ( ) 12f t f t + = ( ]0,4x∈ ( ) ( )f xf x x ′ > ( ) ( ) ( )2016 4 2017 2 2018f f f、 、 ( ) ( ) ( )2 2018 2016 4 2017f f f< < ( ) ( ) ( )2 2018 2016 4 2017f f f> > ( ) ( ) ( )4 2017 2 2018 2016f f f< < ( ) ( ) ( )4 2017 2 2018 2016f f f> > 13.已知数据 的平均数为 2,则数据 的平均数为 . 14.设 ,且 是 与 的等比中项,则 的最小值为 . 15.当双曲线 不是等轴双曲线时,我们把以双曲线 的实轴、虚轴的端点作为顶点 的椭圆称为双曲线 的“伴生椭圆”.则离心率为 的双曲线的“伴生椭圆”的 离心率为 . 16.已知平面区域 , ,在区域 上 随机取一点 ,点 落在区域 内的概率为 . 三.解答题:共70分,解答应写出文字说明,证明过程或演算步骤。第17~21题为必考题,每个考 生都必须作答。第22、23题为选考题,考生根据要求作答。 (一)必考题:共60分。 17.(本小题满分 12 分) 在 中,角 的对边分别为 ,已知 . (1)求 ; (2)若 , 边上的中线 ,求 的面积. 18.(本小题满分 12 分) 在某大学联盟的自主招生考试中,报考文史专业的考生参加了人文基础学科考试科目 “语文”和“数学”的考试. 某考场考生的两科考试成绩数据统计如下图所示,本次 考试中成绩在 内的记为 ,其中“语文”科目成绩在 内的考生有 10 人. (1)求该考场考生数学科目成绩为 的人数; 1 2, , , nx x x 1 22, 2, , 2nx x x+ + + 0, 0a b> > 3 3a 3b 1 1 a b + C C C 3 ( ) 2 2{ , | 4}M x y x y= + ≤ ( ){ , | 2}N x y y x= ≥ − + M A A N ABC∆ , ,A B C , ,a b c cos cos cos 2cos sinC A B A B+ = tanA 2 5b = AB 17CD = ABC∆ ]100,90[ A )90,80[ A A B C D 图 2 E (2)已知参加本场测试的考生中,恰有两人的两科成绩均为 .在至少一科成绩为 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为 的概率. 19.(本小题满分 12 分) 如图 1,在直角梯形 中, , , , 点 为 中点,将 沿 折起, 使平面 平面 ,得到几何 体 ,如图 2 所示. (1)在 上是否存在一点 ,使 平面 ?若存在,证明你的结论, 若不存在,请说明理由; (2)求点 到平面 的距离. 20.(本小题满分 12 分) 已知 , 分别为椭圆 : 的左、右焦点,点 在椭圆 上. (1)求 的最小值; (2)设直线 的斜率为 ,直线 与椭圆 交于 , 两点,若点 在第一象限, 且 ,求 面积的最大值. 21.(本小题满分 12 分) 已知函数 ,其导函数 ,且 , . ABCD 90ADC∠ = ° / /CD AB 1 22AD CD AB= = = E AC ADC∆ AC ADC ⊥ ABC D ABC− CD F / /AD EFB A A A C ABD 1F 2F C 2 2 18 2 x y+ = P C 1 2PF PF⋅ l 1 2 l C A B P 1 2 1PF PF⋅ = − ABP∆ ( ) 3f x ax bx c= + + ( ) 23 3f x x= −′ + ( )0 1f = − ( ) ( )ln 1g x x x mm x = + ≥ BA CD 图 1 E (1)求 的极值; (2)求证:对任意 ,都有 . (二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。 答题时请写清题号并将相应信息点涂黑。 22.(本小题满分 10 分)选修 4-4:坐标系与参数方程 已知曲线 的参数方程为 ( 为参数),以直角坐标系原点 为极点, 轴正半轴为极轴建立极坐标系. (1)求曲线 的极坐标方程; (2)设射线 , ,若 分别与曲线 相交于异于原点的两点 , 求 的面积. 23.(本小题满分 10 分)选修 4-5:不等式选讲 设函数 . (1)解不等式 ; (2) , 恒成立,求实数 的取值范围. ( )f x ( )1 2, 0,x x ∈ +∞ ( ) ( )1 2f x g x≤ C 2 2 2cos 2 2 2sin x y α α = + = + α O x C 1 : 3l πθ = 2 : 6l πθ = 1 2,l l C ,A B ABO∆ ( ) 2 2 1f x x x= − − + ( ) 0f x ≤ x R∀ ∈ ( ) 22 4f x m m− ≤ m 惠州市 2018 届第三次调研考试 文科数学参考答案与评分标准 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D B B C D C D C B A A C 1.【解析】 , , ,故选 D. 2.【解析】 ,所以 ,则 ,故选择 B. 3. 【 解 析 , 解 得 , . 故选 B 4. 【解析】 = .故选 C. 5.【解析】 试题分析: 时, ,但 是不是奇函数,A 错; 命题 的否定是 ,B 错; 中只要有一个为假 命 题 , 则 为 假 命 题 , C 错 ; “ 若 , 则 ” 的 否 命 题 是 “ 若 , 则 ”是正确的,故选 D. 6.【解析】输入 , 经过第一次循环得到 , 经过第二循环得到 , 经过第三次循环得到 ,此时输出 , 故选 C. 考点:程序框图的识别及应用 7.【解析】因为 ,所以 ,所以 ,解 }{ 1 2A x x= − ≤ ≤ }{ 1≥= xxBCR }{ 21 ≤≤= xxBCA R ( ) ( )( ) 1 1 1 1 1 1 1 2 2 2 i ii iz ii i i + − += = = = − +− − + 2 2z = 1 2z = 3 3 4 5 1 2 4a a a q a q+ = + = 3 2q = 9 9 9 10 11 1 2 1 2( )a a a q a q a a q+ = + = + 32 2 16= × = 2a b− = 2(2 )a b− 2 2 4 4 16 4 2 5a b ab+ − = + = 2( )f x x x= + (0) 0f = ( )f x 2 0 0 0: , 1 0p x R x x∃ ∈ − − > 2: , 1 0p x R x x¬ ∀ ∈ − − ≤ ,p q p q∧ 6 πα = 1sin 2 α = 6 πα ≠ 1sin 2 α ≠ 12x = 2 12 1 25, 2x n= × + = = 2 25 1 51, 3x n= × + = = 2 51 1 103, 4x n= × + = = x ( ) ( )1 cos 24f x x θ= + ( ) 1 5 1 5cos 2 cos 24 12 4 6g x x x π πθ θ = − + = − + 2 5 9 6 k π π θ π− + = ( )k Z∈ 得 ,又 ,所以 ,故选 D. 8.【解析】. 因为 ,如图所示经过原点 的直线斜率最大的为直线 与直线 的 交 点 ,故 ,选 C. 9.【解析】由三视图可知该三棱锥底面是边长为 4 的正三角形,面积为 ,高为 4, 则 ,故选 B. 10.【解析】由 ,知 是奇函数,故排除 C,D;当 时, ,从而 A 正确. 11.【解析】根据抛物线的定义,点 P 到准线的距离等于到焦点的距离,则距离之和等于 , 画图可得, 的最小值为圆心 C 与焦点 F 连线与抛物线相交于点 P,则最小值等于 , 圆心 ,得 ,所以最小值为 ,故选 A. 12.【解析】由题意可得: ,则: , 11 18k πθ π= + ( )k Z∈ 2 πθ < 7 18 πθ = − 0 0 yz x −= − ( )0,0 4 0x y+ − = 1x = ( )1,3 max 3 31z = = 4 3 1 16 34 33 4 3V = × × = ( ) ( ) 0f x f x+ − = ( )f x 1 2x = 1 21 1 1 1 1 1( ) ln 1 ln ln 2 ln ln 2 02 2 2 2 2 2f e= − + = + = − = − < PQ PF+ PQ PF+ CF r− (0, 4)C 2 24 1 17CF = + = 17 1− ( ) ( )2 1f t f t + = ( ) ( )2 4 1f t f t+ + = 据此有: ,即函数 是周期为 的周期函数, 构造新函数 ,则 , 则函数 是定义域 内的增函数, 有: ,即: , 利用函数的周期性可得: , 据此可得: . 二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13. 4 14. 4 15. 16. 13.【解析】平均数为 14.【解析】试题分析:因 ,即 ,故 , 所以 ,应填 . 15.【解析】试题分析:设双曲线 C 的方程为 ,所以 , ∴ 双 曲 线 C 的 “ 伴 生 椭 圆 ” 方 程 为 : , ∴ “ 伴 生 椭 圆 ” 的 离 心 率 为 16.【解析】【答案】 【解析】由题意可得,集合 M 表示坐标原点为圆心,2 为半径的圆及其内部,集合 N 表示图中的阴 2 2 ( ) ( )4f t f t= + ( )f x 4 ( ) ( ) ( ], 0,4f xF x xx = ∈ ( ) ( ) ( ) 2 ' 0f x x f xF x x −= > ( )F x ( ]0,4 ( ) ( ) ( )1 2 4 1 2 4 f f f< < ( ) ( ) ( )4 1 2 2 4f f f< < ( ) ( ) ( ) ( ) ( ) ( )2016 4 , 2017 1 , 2018 2f f f f f f= = = ( ) ( ) ( )4 2017 2 2018 2016f f f< < 2 4 π π − ( ) ( ) ( ) ( )1 2 1 22 2 2 2 2 2 4n nx x x x x x n n n + + + + + + + + + += = + = 3)3(33 2 ==⋅ ba 33 =+ba 1=+ ba =+ ba 11 42)11)(( ≥++=++ a b b a baba 4 2 2 2 2 1x y a b − = 2 2 2 23 2a be b aa += = ∴ =, 2 2 2 2 1y x b a + = 2 2 2 22 b a a b a − = = 2 4 π π − 影区域,其中 , 由几何概型公式可得:点 落在区域 内的概率为 . 三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明,演算步骤或证明过程) 17. (本小题满分 12 分) 【答案】(1) ; (2)当 时, ;当 时, . 【解析】试题分析:(1)将 代入化简求值即可;(Ⅱ)在 中,由余弦定理 解 得 或 6,利用面积公式求解即可. 试题解析: (1)由已知得 , ……2 分 所以 , ………4 分 因为在 中, , 所以 , 则 . ……………6 分 (2)由(1)得, , , ……………8 分 在 中, , 代入条件得 ,解得 或 6, ………10 分 当 时, ;当 时, . ………12 分 21 12 2 2 24 2S π π= × − × × = −阴影 A N 2 2 2 2 4p π π π π − −= =× tan 2A = 2c = 1 sin 42ABCS bc A= = 6c = 12ABCS∆ = ( )C A Bπ= − + ACD 2c = ( )cos cos cos cos π cos cosC A B A B A B + = − + + ( )cos cos cos sin sinA B A B A B= − + + = sin sin 2cos sinA B A B= ABC∆ sin 0B ≠ sin 2cosA A= tan 2A = 5cos 5A = 2 5sin 5A = ACD∆ 2 2 2 2 cos2 2 c cCD b b A = + − ⋅ ⋅ ⋅ 2 8 12 0c c− + = 2c = 2c = 1 sin 42ABCS bc A∆ = = 6c = 12ABCS∆ = 18. (本小题满分 12 分) 19. 解:(1)该考场的考生人数为 10÷0.25=40 人. ………2 分 数学科目成绩为 的人数为 40×(1-0.0025×10-0.015×10-0.0375×10×2)=40×0.075=3 人. ………5 分 (2) 语文和数学成绩为 A 的各有 3 人,其中有两人的两科成绩均为 ,所以还有两名同学 只有一科成绩为 . ……………7 分 设这四人为甲、乙、丙、丁,其中甲、乙的两科成绩均为 ,则在至少一科成绩为 的考生 中, 随机抽取两人进行访谈,基本事件为{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁}, {丙,丁}共 6 个, …………… 10 分 设“随机抽取两人,这两人的两科成绩均为 ”为事件 ,则事件 包含的事件有 1 个, 则 . ……………12 分 19. 试题解析:(1)存在 的中点 成立, 连结 , 在 中, ,分别为 , 的中点 ……2 分 为 的中位线 // ………4 分 平面 平面 //平面 ……………6 分 (2) 设点 到平面 的距离为 ⊥ , , ⊥ ⊥ ⊥ , ⊥ ……………7 分 ⊥ 即 ⊥ CD A A A A M A M M 6 1)( =MP F EF BF ACD∆ ,E F AC DC EF∴ ACD∆ AD∴ EF EF ⊆ EFB AD ⊄ EFB AD∴ EFB C ABD h 平面 ABD 平面 CAB 平面 ABD 平面 C=ABAB BC且 BA BC∴ 平面 CAD BC∴ AD AD DC AD∴ 平面 BCD AD BD ………9 分 三棱锥 的高 , ………10 分 即 ………12 分 20. (本小题满分 12 分) 【答案】(1) 的最小值为 ; (2)12. 【解析】试题分析: (1)设 ,由向量数量积的坐标运算求得 ,注意椭圆中 有 ,因此可得最小值; (2)由直线与圆锥曲线相交的弦长公式求得弦长 ,求出 点坐标,再求得 到直线 的距 离 即三角形的高,从而得 面积 由基本不等式可得最大值. 试题解析: (1)有题意可知 , ,设点 则 , , ………2 分 ∴ , ∵点 在椭圆 上,∴ ,即 , ………3 分 ∴ ( ), ………4 分 ∴当 时, 的最小值为 . ………6 分 (注:此问也可用椭圆的参数方程表达点 P 求解) (2)设 的方程 ,点 , , S 2 3ADB∆∴ = B ACD− 2 2BC = S 2ACD∆∴ = B ACD C ADBV− −=V 1 12 2 2 2 33 3 h× × = × × 2 6 3h∴ = 1 2PF PF⋅ 4− ( )0 0,P x y 2 0 1 2 34 4 xPF PF⋅ = − + 02 2 2 2x− ≤ ≤ AB P P AB PAB∆ ( )2 24PABS b b∆ = − ( )1 6,0F − ( )2 6,0F 0 0( , )P x y ( )1 0 06 ,PF x y= − − − ( )2 0 06 ,PF x y= − − 2 2 1 2 0 0 6PF PF x y⋅ = + − ( )0 0,P x y C 2 2 0 0 18 2 x y+ = 2 2 0 0 2 4 xy = − 2 2 2 0 0 1 2 0 32 6 44 4 x xPF PF x⋅ = + − − = − + 02 2 2 2x− ≤ ≤ 0 0x = 1 2PF PF⋅ 4− l 1 2y x b= + ( )1 1,A x y ( )2 2,B x y 由 得 , ………7 分 令 ,解得 . 由韦达定理得 , , 由弦长公式得 , ………8 分 且 ,得 . 又点 到直线 的距离 , ………9 分 ∴ , ………11 分 当且仅当 时,等号成立, ∴ 面积最大值为 2. ……12 分 21.(本小题满分 12 分) 解析:(1)依题意得 , ………2 分 知 在 和 上是减函数,在 上是增函数 ………4 分 ∴ , ………5 分 (2)法 1:易得 时, , 依题意知,只要 由 知,只要 ………7 分 令 ,则 ………8 分 2 2 1 ,2 18 2 y x b x y = + + = 2 22 2 4 0x bx b+ + − = 2 24 8 16 0b b∆ = − + > 2 2m− < < 1 2 2x x b+ = − 2 1 2 2 4x x b= − ( ) ( )2 2 1 2 1 2 11 4 5 44AB x x x x b= + + − = − 1 2 1PF PF⋅ = − ( )2,1P P l 2 1 51 4 b bd = = + ( )221 1 5 42 2 5PAB bS AB d b∆ = = × × − ( )2 24b b= − 2 24 22 b b+ −≤ = 2b = ± PAB∆ ( ) 3 3 1f x x x= − + − ( ) ( )( )23 3 3 1 1f x x x x= − + = − + −′ ( )f x ( ), 1−∞ − ( )1,+∞ ( )1,1− ( ) ( )1 3f x f= − = − 极小值 ( ) ( )1 1f x f= = 极大值 0x > ( ) 1f x = 最大值 ( ) ( )1 ( 0) 1 ln 1 ( 0)mg x x x x m xx ≤ > ⇔ ≤ + ≥ > 1a ≥ 2 2ln 1( 0) ln 1 0( 0)x x x x x x x x≤ + > ⇔ + − ≥ > ( ) 2ln 1 ( 0)h x x x x x= + − > ( ) 2 ln 1h x x x x= + −′ 注意到 ,当 时, ;当 时, , ………9 分 即 在 上是减函数,在 是增函数, ………10 分 即 ,综上知对任意 ,都有 ………12 分 法 2:易得 时, , ………7 分 由 知, ,令 ………8 分 则 ………9 分 注意到 ,当 时, ;当 时, ,………10 分 即 在 上 是 减 函 数 , 在 是 增 函 数 , , 所 以 , 即 . 综上知对任意 ,都有 . ………12 分 法 3: 易得 时, , ………7 分 由 知, , ………8 分 令 ,则 ………9 分 令 ,则 ,………10 分 知 在 递增,注意到 , 所以, 在 上是减函数,在 是增函数,有 ,即 综上知对任意 ,都有 . ……12 分 22. (本小题满分 10 分) 解:(1)∵曲线 的参数方程为 ( )1 0h′ = 1x > ( ) 0h x′ > 0 1x< < ( ) 0h x′ < ( )h x ( )0,1 ( )1,+∞ ( ) ( )1 0h x h= = 最小值 ( ) 0h x ≥ ( )1 2, 0,x x ∈ +∞ ( ) ( )1 2f x g x≤ 0x > ( ) 1f x = 最大值 1a ≥ ( ) 1ln ( 0)g x x x xx ≥ + > ( ) 1ln ( 0)h x x x xx = + > ( ) 2 2 2 1 1ln 1 ln xh x x xx x −= + − = +′ ( )1 0h′ = 1x > ( ) 0h x′ > 0 1x< < ( ) 0h x′ < ( )h x ( )0,1 ( )1,+∞ ( ) ( )1 1h x h= = 最小值 ( ) 1h x = 最小值 ( ) 1g x = 最小值 ( )1 2, 0,x x ∈ +∞ ( ) ( )1 2f x g x≤ 0x > ( ) 1f x = 最大值 1a ≥ ( ) 1ln ( 0)g x x x xx ≥ + > ( ) 1ln ( 0)h x x x xx = + > ( ) 2 1ln 1 ( 0)h x x xx = + − >′ ( ) 2 1ln 1 ( 0)x x xx ϕ = + − > ( ) 3 1 1 0x x x ϕ = + >′ ( )xϕ ( )0,+∞ ( )1 0ϕ = ( )h x ( )0,1 ( )1,+∞ ( ) 1h x = 最小值 ( ) 1g x = 最小值 ( )1 2, 0,x x ∈ +∞ ( ) ( )1 2f x g x≤ C 2 2 2 cos ( 2 2 2 sin x y α α α = + = + 为参数) ∴曲线的普通方程为 即 ……2 分 将 代入并化简得: 即曲线 的极坐标方程为 . …………5 分 (2)由 得到 …………7 分 同理 . ………… 9 分 又∵ ∴ . 即 的面积为 . …………10 分 23. (本小题满分 10 分) 23.解:(1)不等式 ,即 ,即 ,……2 分 ,解得 或 .……3 分 所以不等式 的解集为 或 .……4 分 (2) ……6 分 故 的最大值为 ,……8 分 因为对于 ,使 恒成立. 所以 ,即 , 2 2( 2) ( 2) 8x y− + − = 2 2 4 4 0x y x y+ − − = cos , sinx yρ θ ρ θ= = 4cos 4sinρ θ θ= + C 4cos 4sinρ θ θ= + 3 4cos 4sin πθ ρ θ θ = = + 1 2 2 3OA ρ= = + 2 2 2 3OB ρ= = + 3 6 6AOB π π π∠ = − = 1 sin 4 2 32AOBS OA OB AOB∆ = ∠ = + AOB∆ 4 2 3+ ( ) 0f x ≤ 2 2 1x x− ≤ + 2 24 4 4 4 1x x x x− + ≤ + + 23 8 3 0x x+ − ≥ 1 3x ≥ 3x ≤ − ( ) 0f x ≤ 1{ 3x x ≥ 3}x ≤ − ( )= 2 2 1f x x x− − + = 13, 2 13 1, 22 3, 2 x x x x x x + < − − + − ≤ ≤ − − > ( )f x 1 5 2 2f − = x R∀ ∈ ( ) 22 4f x m m− ≤ 2 52 4 2m m+ ≥ 24 8 5 0m m+ − ≥ 解得 或 ,∴ .……10 分1 2m ≥ 5 2m ≤ − 5 1, ,2 2m ∈ −∞ − +∞ 查看更多