河南广东等省2020届高三普通高等学校招生全国统一考试4月联考数学（理）试题

河南广东等省2020届高三普通高等学校招生全国统一考试4月联考数学（理）试题

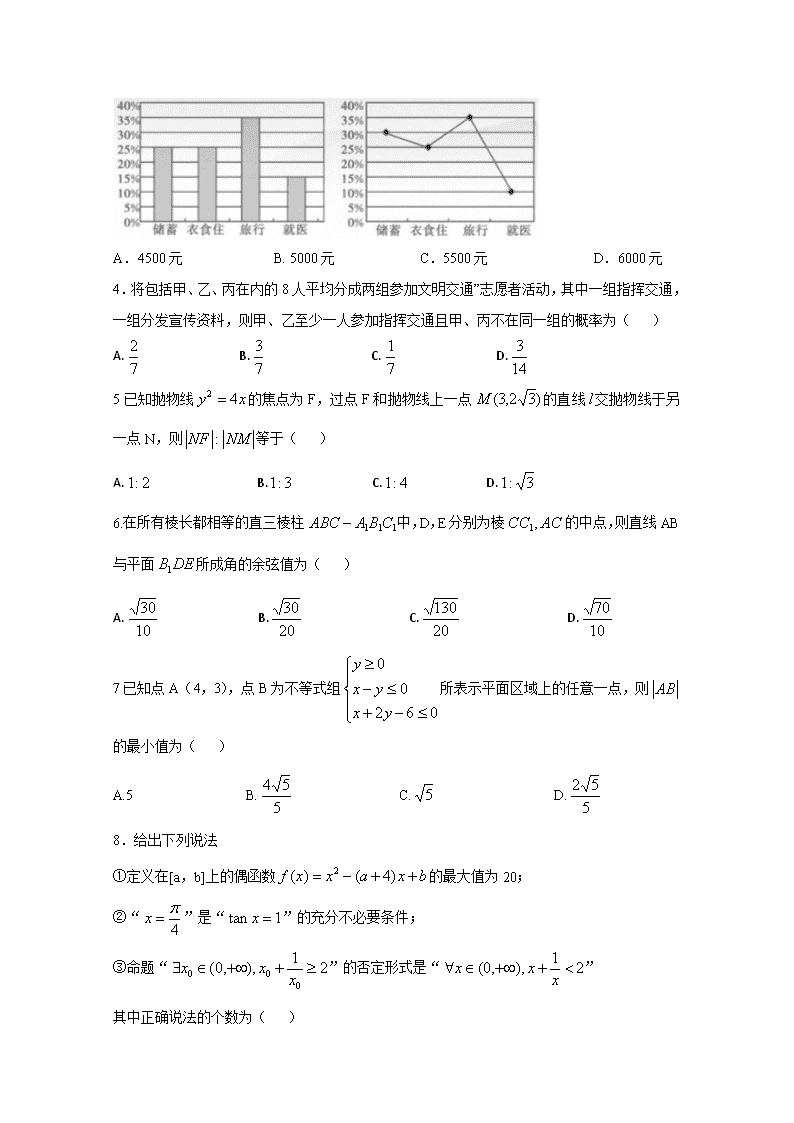
绝密★启用前 试卷类型：B ‎2020年普通高等学校招生全国统一考试·联考 理科数学 本试卷共5页，23小题（含选考题），满分150分，考试用时120分钟．‎ 注意事项：‎ ‎1．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上用2B铅笔将试卷类型（B）填在答题卡相应位置上，将条形码横贴在答题卡右上角“条形码粘贴处”．‎ ‎2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案．答案不能答在试卷上．‎ ‎3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液．不按以上要求作答无效．‎ ‎4选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。答案写在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效．‎ ‎5．考试结束后，请将本试卷和答题卡一并上交。‎ 一、选择题：本题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.设集合，则集合A的真子集有（ ）‎ A．5个 B. 6个 C. 7个 D. 8个 ‎2．已知i是虚数单位，则化简的结果为（ ）‎ A. B. C. D.1 ‎ ‎3.若干年前，某教师刚退休的月退休金为400元，月退休金各种用途占比统计图如下面的条形图该教师退休后加强了体育锻炼，目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元，则目前该教师的月退休金为（ ）‎ A．4500元 B. 5000元 C．5500元 D．6000元 ‎4．将包括甲、乙、丙在内的8人平均分成两组参加文明交通”志愿者活动，其中一组指挥交通，一组分发宣传资料，则甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率为（ ）‎ A. B. C. D.‎ ‎5已知抛物线的焦点为F，过点F和抛物线上一点的直线交抛物线于另一点N，则等于（ ） ‎ A. B. C. D. ‎ ‎6.在所有棱长都相等的直三棱柱中，D，E分别为棱的中点，则直线AB与平面所成角的余弦值为（ ）‎ A. B. C. D.‎ ‎7已知点A（4，3），点B为不等式组所表示平面区域上的任意一点，则的最小值为（ ）‎ A.5 B. C. D.‎ ‎8．给出下列说法 ‎①定义在[a，b]上的偶函数的最大值为20；‎ ‎②“”是“”的充分不必要条件；‎ ‎③命题“”的否定形式是“”‎ 其中正确说法的个数为（ ）‎ A.0 B.1 C.2 D.3‎ ‎9.已知，则间的大小关系为 A. B. C. D.‎ ‎10．元代数学家朱世杰在《算学启蒙》中提及如下问题：今有银一秤一斤十两（1秤=15斤，1斤=16两），令甲、乙、丙从上作折半差分之，问：各得几何?其意思是：现有银一秤一斤十两，现将银分给甲、乙、丙三人，他们三人每一个人所得是前一个人所得的一半.若银的数量不变，按此法将银依次分给7个人，则得银最少的一个人得银（ ）‎ A．9两 B.两 C.两 D.两 ‎11在△ABC中，角A、B、C的对边分别是a、b、c，若，则的最大值为( ) ‎ A. B. C. D.‎ ‎12.已知几为奇函数，为偶函数，且，不等式对恒成立，则的最大值为（ ）‎ A.1 B. C.2 D.‎ 二、填空题：本题共4小题，每小题5分，共20分 ‎13已知向量a=（2，），b=（1，），则b在a方向上的投影等于 .‎ ‎14在△ABC中，∠B=，A、B是双曲线E的左、右焦点，点C在E上，且BC=AB，则E的离心率为 .‎ ‎5已知函数是奇函数，且在上单调减，则的最大值是 .‎ ‎16已知三棱锥A-BCD中，平面ABD⊥平面BCD，BC⊥CD，BC=CD=2，AB=AD=，则三棱锥A-BCD的外接球的体积为 .‎ 三、解答题：共70分解答应写出文字说明、证明过程或演算步骤第次年题为必考题，每个试题考生都必须作答第22、23题为选考题，考生根据要求作答 ‎（一）必考题：共60分 ‎17．（12分）‎ 已知数列{an}的前n项和为Sn，且．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）若数列的前n项和为Tn，证明： ．‎ ‎18．（12分）‎ 如图，在以A，B，C，D，E，F为顶点的五面体中，四边形ABEF为正方形，AF⊥DF，AF=FD，∠DFE=∠CEF=45．‎ ‎（1）证明DC∥FE；‎ ‎（2）求二面角D-BE-C的平面角的余弦值．‎ ‎19．（12分）‎ 已知点P在圆O：x2+y2=9上，点P在x轴上的投影为Q，动点M满足．‎ ‎（1）求动点M的轨迹E的方程；‎ ‎（2）设G（-3，0），H（3，0），过点F（1，0）的动直线l与曲线E交于A、B两点，问直线AG与直线BH的斜率之比是否为定值?若为定值，求出该定值；若不为定值，试说明理由．‎ ‎20．（12分）‎ 某县为了帮助农户脱贫致富，鼓励农户利用荒地山坡种植果树，某农户考察了三种不同的果树苗A、B、C．经过引种实验发现，引种树苗A的自然成活率为0.7，引种树苗B、C的自然成活率均为p（0.6≤p≤0.8）‎ ‎（1）任取树苗A、B、C各一棵，估计自然成活的棵数为X，求X的分布列及其数学期望；‎ ‎（2）将（1）中的数学期望取得最大值时p的值作为B种树苗自然成活的概率，该农户决定引种n棵B种树苗，引种后没有自然成活的树苗有75%的树苗可经过人栽培技术处理，处理后成活的概率为0.8，其余的树苗不能成活．‎ ‎①求一棵B种树苗最终成活的概率；‎ ‎②若每棵树苗引种最终成活可获利400元，不成活的每棵亏损80元该农户为了获利期望不低于10万元，问至少要引种种树苗多少棵?‎ ‎21．（12分）‎ 已知函数f（x）=（a-1）x+xlnx的图象在点A（e2，f（e2））（e为自然对数的底数）处的切线斜率为4‎ ‎（1）求实数a的值；‎ ‎（2）若m∈Z，且m（x-1）1恒成立，求m的最大值．‎ ‎（二）选考题：共10分．请考生在22、23题中任选一题作答．如果多做，则按所做的第一题记分．‎ ‎22．[选修4-4：坐标系与参数方程]（10分）‎ 以坐标原点为极点，以x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为，直线l的参数方程为（t为参数）．‎ ‎（1）点A在曲线C上，且曲线C在点A处的切线与直线：x+2+1=0垂直，求点A的直角坐标；‎ ‎（2）设直线l与曲线C有且只有一个公共点，求直线l的斜率的取值范围．‎ ‎23．[选修4-5：不等式选讲]（10分）‎ 设函数f（x）=|x-1|+2|x+1|，x∈R ‎（1）求不等式f（x）<5的解集；‎ ‎（2）若关于x的不等式在实数范围内解集为空集，求实数t的取值范围