2018-2019学年河北省灵寿县高二下学期5月月考数学（理）试题 Word版

2018-2019学年河北省灵寿县高二下学期5月月考数学（理）试题 Word版

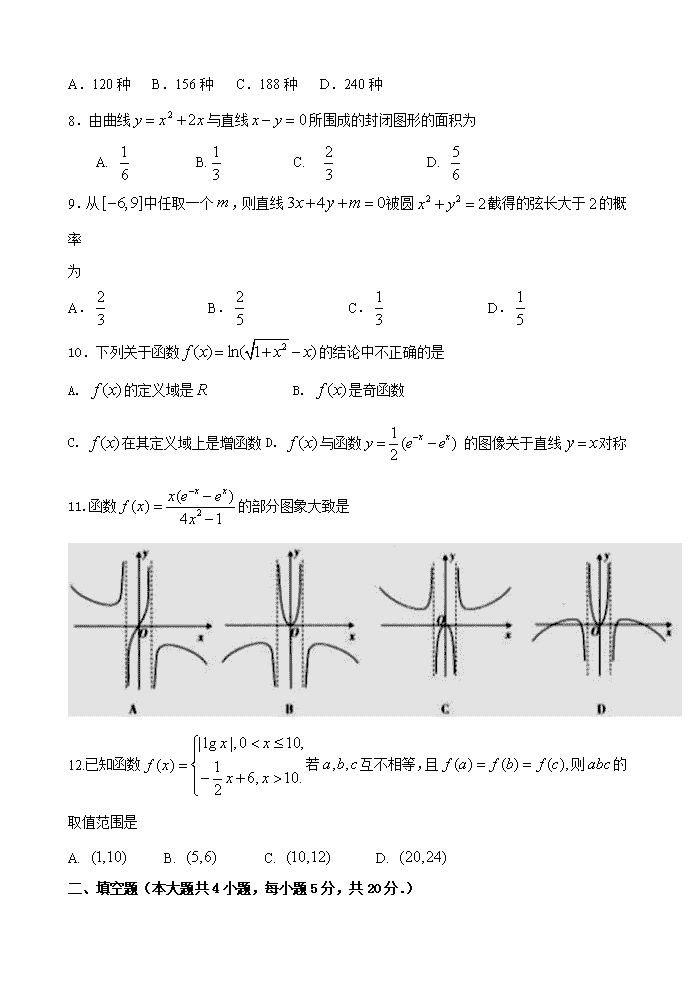
灵寿县2018～2019学年度第二学期5月月考 ‎ 高二数学（理）试题 一、选择题（本大题共12小题，每小题5分，共60分．）‎ ‎1．已知集合,则 A. B. C. D. ‎ ‎2．复数的虚部是 A. B. C. D. ‎ ‎3．函数的一个零点落在下列哪个区间 A. B. C. D. ‎ ‎4．若二次函数对于一切实数都有成立，则以下选项有可能成立的为 A． B． ‎ C. D．‎ ‎5．下列说法正确的是 A. 命题“若，则”的否命题为“若，则”‎ B. 命题“,”的否定是“R,”‎ C. ,使得 D.“”是“”的充分条件 ‎6.设且，则“”是“”的 A.必要不充分条件 B.充要条件 C.既不充分也不必要条件 D.充分不必要条件 ‎7．某校毕业典礼由6个节目组成，考虑整体效果，对节目演出顺序有如下要求：节目甲必须排在前三位，且节目丙、丁必须排在一起，则该校毕业典礼节目演出顺序的编排方案共有 A．120种 B．156种 C．188种 D．240种 ‎8．由曲线与直线所围成的封闭图形的面积为 A. B. C. D. ‎ ‎9．从中任取一个，则直线被圆截得的弦长大于的概率 为 A． B． C． D．‎ ‎10．下列关于函数的结论中不正确的是 A. 的定义域是 B. 是奇函数 C. 在其定义域上是增函数 D. 与函数 的图像关于直线对称 ‎11.函数的部分图象大致是 ‎12.已知函数若互不相等，且则的取值范围是 A. B. C. D. ‎ 二、填空题（本大题共4小题，每小题5分，共20分．）‎ ‎13.______________.‎ ‎14.用两个，一个，一个，可组成不同四位数的个数是________.‎ ‎15.的展开式中，二项式系数最大的项的系数是________．（用数字作答）‎ ‎16．已知函数，满足和是偶函数，且，设，则_________.‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17. （本小题满分12分） 已知R，命题：对任意，不等式恒成立；命题：存在，使得成立.‎ ‎（Ⅰ）若为真命题，求的取值范围；‎ ‎（Ⅱ）若且为假，或为真，求的取值范围；‎ ‎18.（本小题满分12分）‎ 函数的定义域为,且满足对于任意,有 （Ⅰ）求的值；‎ ‎（Ⅱ）判断的奇偶性并证明你的结论；‎ ‎（III）若，且在上是增函数，求的取值范围.‎ ‎19.（本小题满分12分）‎ 机动车的尾气是雾霾颗粒组成的最主要的成分，最新的数据显示，某市雾霾颗粒中机动车尾气占22.2%，为减少汽车尾气排放,提高空气质量,各地纷纷推出汽车尾号限行措施.为做好此项工作，市交警支队对市区各交通枢纽进行调查统计，表中列出了某交通路口单位时间内通过的1000辆汽车的车牌尾号记录：‎ 组名 尾号 频数 频率 第一组 ‎1、3‎ ‎250‎ ‎0.25‎ 第二组 ‎0、4、6‎ ‎200‎ ‎0.2‎ 第三组 ‎5、7、9‎ ‎250‎ ‎0.25‎ 第四组 ‎2、8‎ ‎300‎ ‎0.3‎ 请根据图表提供的信息计算：‎ ‎（Ⅰ）若采用分层抽样的方法从这1000辆汽车中抽出20辆，再从这20辆中任选4辆，求选取的4辆车中恰有2辆尾号为偶数的概率；‎ ‎（Ⅱ）以频率代替概率，在此路口随机抽取4辆汽车，奖励汽车用品.用表示车尾号在第一组的汽车数目，求的分布列和数学期望.‎ ‎20.（本小题满分12分）‎ 随着互联网的发展，网上购物越来越受到人们的喜爱，各大购物站为增加收入，促销策略越来越多样化，促销费用也不断增加，下表是某购物站2018年1-8月促销费用(万元)和产品销量(万件)的具体数据：‎ 月份 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 促销费用 ‎2‎ ‎3‎ ‎6‎ ‎10‎ ‎13‎ ‎21‎ ‎15‎ ‎18‎ 产品销量 ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎5‎ ‎4‎ ‎（Ⅰ）根据数据可知与具有线性相关关系，请建立关于的回归方程(系数精确到)；‎ ‎（Ⅱ）已知6月份该购物站为庆祝成立1周年，特制定奖励制度：以(单位：件)表示日销量，，则每位员工每日奖励100元；，则每位员工每日奖励150元；，则每位员工每日奖励200元.现已知该站6月份日销量服从正态分布，请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位).‎ 参考数据：，，其中，分别为第个月的促销费用和产品销量，.‎ 参考公式：(1)，.‎ (1) 若,则.‎ ‎21.（本小题满分12分）选修4-4：坐标系与参数方程 已知平面直角坐标系中，椭圆的方程为，点，直线的参数方程为.‎ ‎（Ⅰ）设直线与的正半轴分别相交于两点，求的最小值并写出此时直线的普通方程；‎ ‎（Ⅱ）写出椭圆的参数方程，并在椭圆上求一点,使点到（Ⅰ）中所得直线的距离最小.‎ ‎22.（本小题满分10分）选修4-4：坐标系与参数方程 在平面直角坐标系中，曲线的参数方程为，（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，已知直线的极坐标方程为．‎ ‎（Ⅰ）求曲线的极坐标方程；‎ ‎（Ⅱ）若直线与直线交于点，与曲线交于两点．且，求．‎ 数学（理）答案 DDBCB CAAAC BC , 9, -160, ‎ ‎17. 解：（Ⅰ）∵对任意x∈[0,1],不等式2x－2≥m2－3m恒成立,‎ ‎∴（2x－2）min≥m2－3m．即m2－3m≤－2．解得1≤m≤2．‎ 因此,若p为真命题时,m的取值范围是[1,2]．‎ ‎（Ⅱ）存在x∈[－1,1],使得m≤x成立,∴m≤1,‎ 命题q为真时,m≤1．∵p且q为假,p或q为真,‎ ‎∴p,q中一个是真命题,一个是假命题．‎ 当p真q假时,则解得1＜m≤2;‎ 当p假q真时, 即m＜1．‎ 综上所述,m的取值范围为（－∞,1）∪（1,2]．‎ ‎18.解：（1）因对于任意,有 所以令，得，∴；‎ （2） 令，得，∴‎ 令，得∴，所以为偶函数；‎ ‎（3）依题设有，，‎ 又，即 因为为偶函数，所以 又在上是增函数，所以 解上式，得或或 所以的取值范围为 ‎19．解（Ⅰ）第一、二、三、四组应抽取的汽车分别为5辆、4辆、5辆、6辆.‎ ‎20辆车中尾号为偶数的有10辆，所以4辆车中恰有2辆的概率为 ‎……6分 ‎（Ⅱ）在此路口随机抽取一辆汽车，该辆车的车尾号在第一组的概率为.……8分 由题意知，则，.‎ 的分布列为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎……………………10分 ‎……………………12分 ‎20.解：（Ⅰ）由题可知， ‎ 将数据代入得 ‎ ‎ 所以关于的回归方程 ‎ ‎（Ⅱ）由题6月份日销量服从正态分布，则 日销量在的概率为， ‎ 日销量在的概率为， ‎ 日销量的概率为， ‎ 所以每位员工当月的奖励金额总数为 元. ‎ ‎21.解： （Ⅰ）由，令得；令得，‎ 由参数的几何意义可得：，‎ 所以，当且仅当时等号成立；此时直线的普通方程为.‎ ‎（Ⅱ）椭圆的参数方程为，设,点到直线：的距离，其中； 当且仅当时取“=”,‎ 此时，所以点为所求.‎ ‎22.解：（1）∵，∴，故曲线的极坐标方程为.‎ ‎（2）将代入得.‎ 将代入，‎ 得，则，则，∴.‎