2018-2019学年江苏省东台市创新学校高二4月检测数学（理）试题 Word版

2018-2019学年江苏省东台市创新学校高二4月检测数学（理）试题 Word版

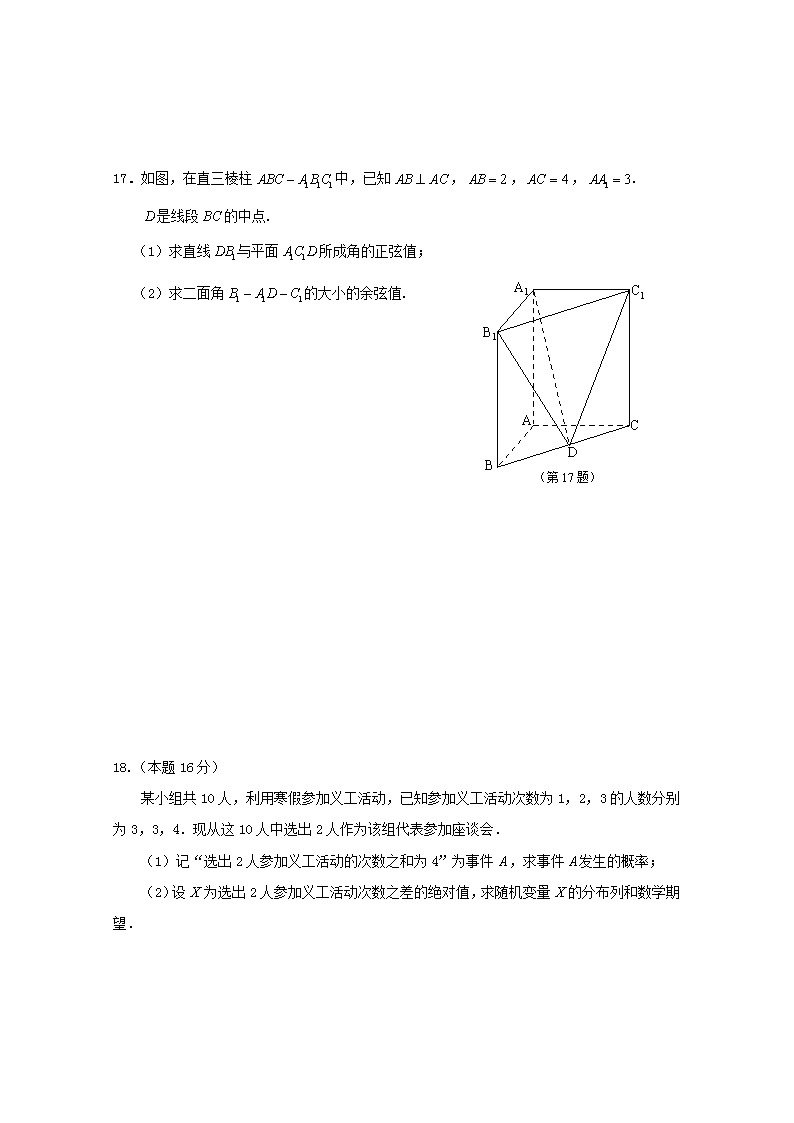
东台创新高级中学 2018-2019 学年度第二学期 2017 级数学 4 月份检测试卷（理科） （考试时间：120 分钟 满分：160 分） 命题人： 李飞 命题时间：4 月 20 一、填空题：（本大题共 14 小题，每小题 5 分，计 70 分.请把答案填写在答题纸的指定位置 上．） 1．已知集合 ， ，若 ，则实数 a 的值为 ▲ ． 2．已知复数 满足 （ 为虚数单位），则复数 的模为 ▲ ． 3.设实数 满足 则 的最大值为 ▲ 4.工人甲在某周五天的时间内，每天加工零件的个数用茎叶图表示如下图(左边一列的 数字表示零件个数的十位数，右边的数字表示零件个数的个位数)，则该组数据的 方差 的值为 ▲ ． 5．函数 的定义域为 ． 6.根据如图所示的伪代码，当输出 的值为 时，则输入的 的值为 7.已知函数 ，若在区间 上任取一个实数 ，则使 成立 的概率为 ． 8.函数 的单调增区间是 {2 3}A = ， {1 1 }B a= −， {2}A B = z i 1 iz = + i iz − ，x y 0 1 2 1 ≥ ， ≤ ， ≥ ， x y x y x y −  +  + 3 2x y+ 2s 1( ) 2 8xf x −= − y 1 2 x ( ) 2 2 3f x x x= − + + [ ]4,4− 0x ( )0 0f x ≥ lny x x= − 1 8 7 2 2 1 2 （第 4 题） Read x If 0≤x Then 12 +← xy Else 2 1 −← xy End If Print y （第 4 题） Read x If 0≤x Then 12 +← xy Else 2 1 −← xy End If Print y （第 6 题） 9.已 9.已知函数 ，若函数 为奇函数，则实数 . 10.已知双曲线 ，则点 到双曲线 的渐近线的距离为_______. 11.设命题 ；命题 ，那么是的_______条件（选填“充分不必要”、“必 要不充分”、“充要”、“既不充分也不必要”）． 12. 在 中，角 所对的边分别为 ，若 ，则 _______. 13.已知函数 与函数 的图象交于 三点，则 的面积为 ________. 14.已知实数 ，若曲线 上存在某点处的切线斜率不大于 ，则 a 的最小值为 ． 二、解答题：(本大题共 6 小题，共计 90 分，请在答题纸指定区域内作答，解答时应写出文 字说明、证明过程或演算步骤．) 15.（本题 14 分） 已知数列{an}满足 an＋1＝ 1 2a2n－ 1 2nan＋1(n∈N*)，且 a1＝3. (1)计算 a2，a3，a4 的值， (2)由此猜想数列{an}的通项公式，并给出证明； (3) 求证：当 n≥2 时，ann≥4nn. 16. （本题 14 分） 设点 在矩阵 对应变换作用下得到点 ． （1）求矩阵 的逆矩阵 ； （2）若曲线 C 在矩阵 对应变换作用下得到曲线 ，求曲线 C 的 方程． ax xxf +=)( 1)2( −+= xfy =a 0>a 21( ) ln ( 2) +12f x x ax a x= + − + 5− ( )x y， M (2 3 )x y， M 1−M 1−M 2 2 1C x y′ + =： 17．如图，在直三棱柱 中，已知 ， ， ， . 是线段 的中点. （1）求直线 与平面 所成角的正弦值； （2）求二面角 的大小的余弦值. 18.（本题 16 分） 某小组共 10 人，利用寒假参加义工活动，已知参加义工活动次数为 1，2，3 的人数分别 为 3，3，4．现从这 10 人中选出 2 人作为该组代表参加座谈会． （1）记“选出 2 人参加义工活动的次数之和为 4”为事件 ，求事件 发生的概率； （2）设 为选出 2 人参加义工活动次数之差的绝对值，求随机变量 的分布列和数学期 望． 1 1 1ABC A B C− AB AC⊥ 2AB = 4AC = 1 3AA = D BC 1DB 1 1AC D 1 1 1B A D C− − A A X X A B C D A1 B1 C1 （第 17 题） 19.（本小题满分 16 分） 已知椭圆 的左右焦点坐标为 ，且椭圆 经过点 。 (1)求椭圆 的标准方程； (2)设点 是椭圆 上位于第一象限内的动点， 分别为椭圆 的左顶点和下顶点，直线 与 轴交于点 ，直线 与轴交于点 ，求四边形 的面积。 20.（本小题满分 16 分） 已知函数 ，其中 为自然对数的底数， ． （1）讨论函数 的单调性，并写出相应的单调区间； （2）已知 ， ，若 对任意 都成立，求 的最大值； （3）设 ，若存在 ，使得 成立，求 的取值范围． ( ) e ( 1)xf x a x= − + e a∈R ( )f x 0a > b∈R ( )≥f x b x∈R ab ( ) ( e)g x a x= + 0x ∈R 0 0( ) ( )f x g x= a 高二数学 4 月份月考答案(理科) 一、填空题 1. -1 ． 2. 3. 3 4． 5. 6. 4 7． 8. ___ _____． 9. -2 10. 11. 充分不必要 12. 13. 14． 9 二、解答题 15．：(1)解　a2＝4，a3＝5，a4＝6，猜想：an＝n＋2(n∈N*)． ①当 n＝1 时，a1＝3，结论成立； 5 ②假设当 n＝k(k≥1，k∈N*)时，结论成立，即 ak＝k＋2， 则当 n＝k＋1 时，ak＋1＝ 1 2a2k－ 1 2kak＋1＝ 1 2(k＋2)2－ 1 2k(k＋2)＋1＝k＋3＝(k＋1)＋2， 即当 n＝k＋1 时，结论也成立． 由①②，得数列{an}的通项公式为 an＝n＋2(n∈N*)． 10 (2)证明　原不等式等价于 (1＋ 2 n )n≥4. 显然，当 n＝2 时，等号成立． 当 n>2 时，(1＋ 2 n )n＝C0n＋C1n2 n＋C2n(2 n )2＋…＋Cnn(2 n )n>C0n＋C1n2 n＋C2n(2 n )2＝5－ 2 n>4. 综上所述，当 n≥2 时，ann≥4nn. 16.（1） ， ，所以 ． （2）设曲线 上任意一点 在矩阵 对应变换作用下得到点 ， 则 ，所以 ． 又点 在曲线 上，所以 ，即 ． 5 22 5 ),4[ +∞ 2 1 ),1( +∞ 2 0 0 3  =   M det( ) 6=M 1 3 10 06 2 12 00 36 −        = =          M C ( )x y， 1−M ( )x y′ ′， 1 02 10 3 x x y y   ′     =     ′      1 2 1 3 x x y y  ′ =  ′ = ， ( )x y′ ′， C′ 2 2( ) ( ) 1x y′ ′+ = 22 14 9 yx + = 所以曲线 的方程为 ． 17,解：因为在直三棱柱 中， ，所以分别以 、 、 所在的直线 为 轴、 轴、 轴，建立空间直角坐标系， 则 ． 因为 是 的中点，所以 ， …… 2 分 （1）因为 ，设平面 的法向量 ， 则 ，即 ，取 ， 所以平面 的法向量 ，而 ， 所以 ， 所以直线 与平面 所成角的正弦值为 ． …… 7 分 （2） ， ，设平面 的法向量 ， 则 ，即 ，取 ，平面 的法向量 ， 所以 ， 二面角 的大小的余弦值 ． …… 14 分 18.解：（1）由已知有 ，所以事件 A 的发生的概率为 ．…5 分 （2）随机变量 X 的所有可能的取值为 0，1，2． … ； ； C 22 14 9 yx + = 1 1 1ABC A B C− AB AC⊥ AB AC 1AA x y z 1 1 1(0,0,0), (2,0,0), (0,4,0), (0,0,3), (2,0,3), (0,4,3)A B C A B C D BC (1,2,0)D 1 1 1(0,4,0), (1,2, 3)AC A D= = −  1 1AC D 1 1 1 1( , , )n x y z= 1 1 1 1 1 0 0 n AC n A D  ⋅ = ⋅ =     1 1 1 1 4 0 2 3 0 y x y z =  + − = 1 1 1 3 0 1 x y z =  =  = 1 1AC D 1 (3,0,1)n = 1 (1, 2,3)DB = − 1 1 1 1 1 1 3 35cos , 35 n DBn DB n DB ⋅< >= = ⋅      1DB 1 1AC D 3 35 35 1 1 (2,0,0)A B = 1 (1, 2,3)DB = − 1 1B A D 2 2 2 2( , , )n x y z= 2 1 1 2 1 0 0 n A B n DB  ⋅ = ⋅ =     2 2 2 2 2 0 2 3 0 x x y z =  − + = 2 2 2 0 3 2 x y z =  =  = 1 1B A D 2 (0,3,2)n = 1 2 1 2 1 2 130cos , 65 n nn n n n ⋅< >= = ⋅      1 1 1B A D C− − 130 65 1 1 2 3 4 3 2 10 1( ) 3 C C CP A C += = 1 3 2 2 2 3 3 4 2 10 4( 0) 15 C C CP X C + += = = 1 1 1 1 3 3 3 4 2 10 7( 1) 15 C C C CP X C += = = ． …10 分 所以随机变量 X 的分布列为 X 0 1 2 P 　　　　　　　　　　　　　　　　　　　 分 数学期望 ． 　　　　　　　　 ………16 分 19.【答案】（1） ；（2） 。 【解析】 【分析】 （1）利用椭圆定义可得 a 值，结合 c 值即可得出； （2）设 ，由 三点共线可得 ， 同理得 ，进而 ，结合点在椭圆上 可得结果. 【详解】(1)因为椭圆焦点坐标为 ，且过点 ， 所以 ，所以 ， 从而 ， 故椭圆的方程为 。 6 (2)设点 ， ， ， 因为 ，且 三点共线，所以 ，解得 ， 所以 ， 1 1 3 4 2 10 4( 2) 15 C CP X C = = = 4 15 7 15 4 15 ( ) 1E X = 同理得 ， 因此 ， ， 因为点 在椭圆上，所以 ，即 ， 代入上式得： 。 16 20 解：（1）由 ，知 ． 若 ，则 恒成立，所以 在 上单调递增； 若 ，令 ，得 ， 当 时， ，当 时， ， 所以 在 上单调递减；在 上单调递增． 6 （2）由（1）知，当 时， ． 因为 对任意 都成立，所以 ， 所以 ． 设 ，（ ），由 ， 令 ，得 ， 当 时， ，所以 在 上单调递增； 当 时， ，所以 在 上单调递减， 所以 在 处取最大值，且最大值为 ． 所以 ，当且仅当 ， 时， 取得最大值为 ． 10 （3）设 ，即 ( ) e ( 1)xf x a x= − + ( ) exf x a′ = − 0a ≤ ( ) 0f x′ > ( )f x ( )−∞ + ∞， 0a > ( ) 0f x′ = lnx a= lnx a< ( ) 0f x′ < lnx a> ( ) 0f x′ > ( )f x ( ln )a−∞， (ln )a + ∞， 0a > min ( ) (ln ) lnf x f a a a= = − ( )f x b≥ x∈R lnb a a−≤ 2 lnab a a−≤ 2( ) lnt a a a= − 0a > 2 1( ) (2 ln ) (2ln 1)t a a a a a aa ′ = − + ⋅ = − + ( ) 0t a′ = 1 2ea −= 1 20 ea −< < ( ) 0t a′ > ( )t a ( )1 20 e − ， 1 2ea −> ( ) 0t a′ < ( )t a ( )1 2e − ∞，+ ( )t a 1 2ea −= 1 2e 2 1ln 2eab a a−≤ ≤ 1 2ea −= 1 21 e2b −= ab 1 2e ( ) ( ) ( )F x f x g x= − ( ) e e 2xF x x ax a= − − − 题设等价于函数 有零点时的 的取值范围． ① 当 时，由 ， ，所以 有零点． ② 当 时，若 ，由 ，得 ； 若 ，由（1）知， ，所以 无零点． ③ 当 时， ， 又存在 ， ，所以 有零点． 16 ( )F x a 0a≥ (1) 3 0F a= − ≤ 1( 1) e e 0F a−− = + + > ( )F x e 02 a− <≤ 0x ≤ e 2 0a+ ≥ ( ) e (e 2 ) 0xF x a x a= − + − > 0x > ( ) (2 1) 0F x a x= − + > ( )F x e 2a < − (0) 1 0F a= − > 0 1 0e 2 ax a −= <+ 0 0( ) 1 (e 2 ) 0F x a x a< − + − = ( )F x