数学文卷·2019届安徽省定远重点中学高二上学期期末考试（2018-02）

数学文卷·2019届安徽省定远重点中学高二上学期期末考试（2018-02）

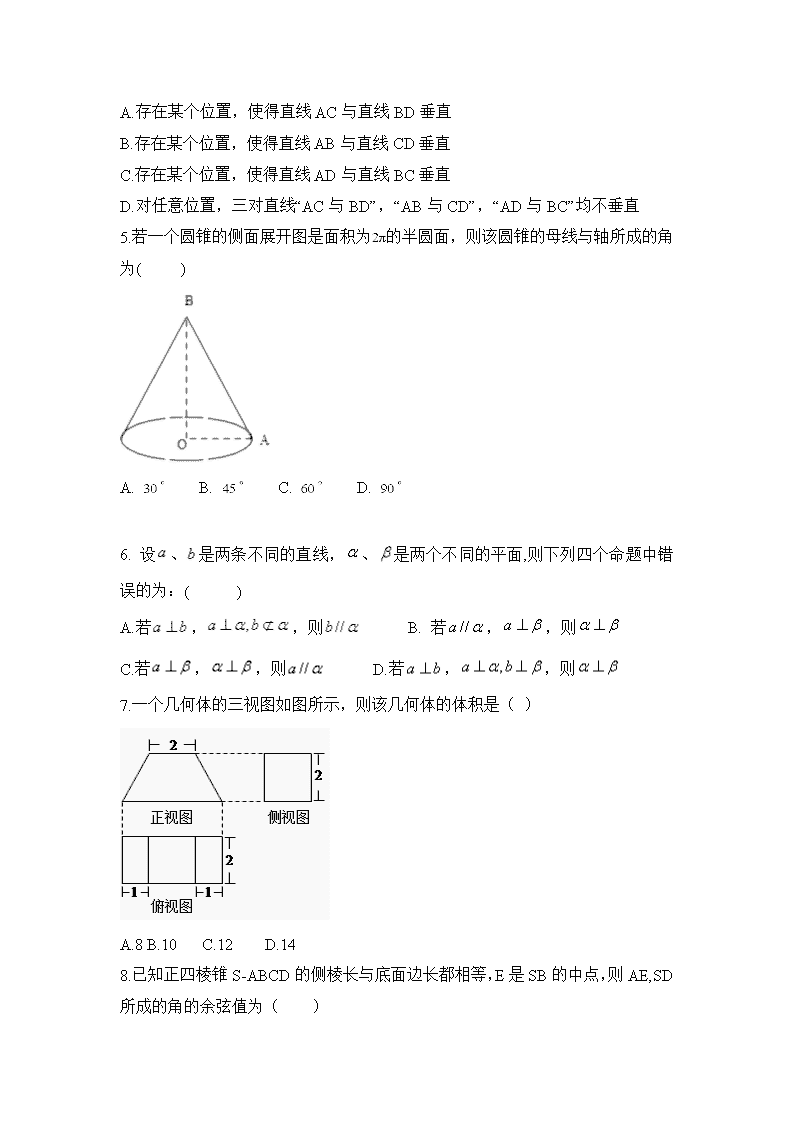
定远重点中学2017-2018学年第一学期期末考试 高二（文科）数学试题 注意事项：‎ ‎1．答题前在答题卡、答案纸上填写好自己的姓名、班级、考号等信息 ‎2．请将第I卷（选择题）答案用2B铅笔正确填写在答题卡上；请将第II卷（非选择题）答案黑色中性笔正确填写在答案纸上。‎ 第I卷（选择题60分）‎ 一、选择题(本大题共12个小题，每小题5分，共60分。) ‎ ‎1.若正棱锥底面边长与侧棱长相等，则该棱锥一定不是（　　） A.三棱锥  B.四棱锥 C.五棱锥 D.六棱锥 ‎2.已知M是正四面体ABCD棱AB的中点，N是棱CD上异于端点C，D的任一点，则下列结论中，正确的个数有（　　） （1）MN⊥AB； （2）若N为中点，则MN与AD所成角为60°； （3）平面CDM⊥平面ABN； （4）不存在点N，使得过MN的平面与AC垂直． A.1 B.2 C.3 D.4‎ ‎3.a，b，c表示直线，M表示平面，给出下列四个命题：‎ ‎①若a∥M，b∥M，则a∥b； ‎ ‎②若b⊂M，a∥b，则a∥M； ‎ ‎③若a⊥c，b⊥c，则a∥b； ‎ ‎④若a⊥M，b⊥M，则a∥b． ‎ 其中正确命题的个数有（ ） ‎ A.0个 B.1个 C.2个 D.3个 ‎ ‎4.已知矩形ABCD，AB=1，BC= ． 将△‎ ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中（　　） A.存在某个位置，使得直线AC与直线BD垂直 B.存在某个位置，使得直线AB与直线CD垂直 C.存在某个位置，使得直线AD与直线BC垂直 D.对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直 ‎5.若一个圆锥的侧面展开图是面积为的半圆面，则该圆锥的母线与轴所成的角为( )‎ A. B. C. D. ‎ ‎6. 设、是两条不同的直线，、是两个不同的平面,则下列四个命题中错误的为：( )‎ A.若，，则 B. 若，，则 ‎ C.若，，则 D.若，，则 ‎7.一个几何体的三视图如图所示，则该几何体的体积是（ ） A.8 B.10 C.12 D.14‎ ‎8.已知正四棱锥S-ABCD的侧棱长与底面边长都相等，E是SB的中点，则AE,SD所成的角的余弦值为（ 　‎ ‎ ） A. B. C. D. ‎ ‎9.设平面与平面相交于直线 ， 直线在平面内，直线在平面内，且 ， 则“”是“”的(　　) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎ ‎10.如图，在正三棱柱ABC－A1B1C1中，AB＝2．若二面角C－AB－C1的大小为60°，则异面直线A1B1和BC1所成角的余弦值为（ ） A. B. C. D.‎ ‎11.某个长方体被一个平面所截，得到几何体的三视图 如图所示，则这个几何体的体积为(　　)‎ A. 4 B. ‎ C. D. 8‎ ‎12. 如图，直三棱柱的六个顶点都在半径为1的半球面上，AB=AC，侧面是半球底面圆的内接正方形，则侧面的面积为（ ） A.2 B.1 C. D. ‎ 第II卷（非选择题90分）‎ 二、填空题 ‎13.已知球的表面积为,用一个平面截球，使截面圆的半径为, 则截面与球心的距离是 ．‎ ‎14.如图，网格纸上小正方形的边长为，粗实线画出的是某几何体的三视图，则该几何体的表面积为__．‎ ‎15.如图正方体ABCD－A1B1C1D1中，与AD1异面且与AD1所成的角为90°的面对角线(面对角线是指正方体各个面上的对角线)共有________条.‎ ‎16.四棱锥中，底面是边长为的正方形，侧面是以为斜边的等腰直角三角形，若，则四棱锥的体积取值范围为_____．‎ 三、解答题 ‎17.如图，边长为的正方形ADEF与梯形ABCD所在的平面互相垂直，其中AB∥CD，AB⊥BC，DC=BC=AB=1，点M在线段EC上． （Ⅰ）证明：平面BDM⊥平面ADEF； （Ⅱ）判断点M的位置，使得三棱锥B﹣CDM的体积为 ． ‎ ‎18.如图，在正方体ABCD﹣A1B1C1D1的棱长为a，若E为棱AB的中点， ①求四棱锥B1﹣BCDE的体积 ②求证：面B1DC⊥面B1DE． ‎ ‎19.如图，在底面是矩形的四棱锥中，⊥平面，,是的中点.‎ ‎（1）求证：平面；‎ ‎（2）求证：平面⊥平面.‎ ‎20.已知三棱柱中，平面⊥平面，⊥，．‎ ‎（1）求证：⊥平面；‎ ‎（2）求平面与平面所成二面角的余弦值．‎ ‎21.如图，在直三棱柱中，是的中点.‎ ‎（1）证明：平面；‎ ‎（2）若，求证：.‎ ‎22.如图，在四棱锥中， ， ∥， ， ， ， .‎ ‎(1)求证：平面平面；‎ ‎(2)若，三棱锥与的体积分别为，求的值．‎ 定远重点中学2017-2018学年第一学期期末考试 高二（文科）数学试题答案 一、选择题 ‎ ‎1. D2. C3.B4. B5..A6.C7. C8. C9.A10. D11.D12.C ‎ 二、填空题 ‎13. ‎ ‎14.‎ ‎15. 1条 ‎16. ‎ 三、解答题 ‎17.‎ 证明：（Ⅰ）∵DC=BC=1，DC⊥BC， ∴BD=， ∵AD=，AB=2， ‎ ‎∴AD2+BD2=AB2 ， ∴∠ADB=90°， ∴AD⊥BD， ∵平面ADEF⊥平面ABCD，ED⊥AD，平面ADEF∩平面ABCD=AD， ∴ED⊥平面ABCD， ∴BD⊥ED， ∵AD∩DE=D， ∴BD⊥平面ADEF， ∵BD⊂平面BDM， ∴平面BDM⊥平面ADEF； （Ⅱ）解：如图，在平面DMC内，过M作MN⊥DC，垂足为N，则MN∥ED， ∵ED⊥平面ABCD， ∴MN⊥平面ABCD， ∵VB﹣CDM=VM﹣CDB=， ∴XX1X1XMN=， ∴MN=， ∴=， ∴CM=CE， ∴点M在线段CE的三等分点且靠近C处． ‎ ‎18. .证明：①由正方形的性质可得B1B平面BEDC， ∴四棱锥B1﹣BCDE的体积V=•S梯形BCDE•B1B=•（a+a）•a•a=； ‎ ‎②取B1D的中点O，设BC1∩B1C=F，连接OF， ∵O，F分别是B1D与B1C的中点，∴OF∥DC，且OF=DC， 又∵E为AB中点，∴EB∥DC，且EB=DC， ∴OF∥EB，OF=EB，即四边形OEBF是平行四边形，∴OE∥BF， ∵DC⊥平面BCC1B1 ， BC1⊂平面BCC1B1 ， ∴BC1⊥DC，∴OE⊥DC． 又BC1⊥B1C，∴OE⊥B1C，又∵DC⊂平面B1DC，B1C⊂平面B1DC，DC∩B1C=C， ∴OE⊥平面B1DC，又∵OE⊂平面B1DE，∴平面B1DC⊥面B1DE． ‎ ‎19. ‎ ‎（1）连结交于，连结，则是的中位线，所以，‎ 又平面，平面，‎ 平面；‎ ‎（2）， ‎ 而 ，‎ 又 ‎ ‎20. ‎ ‎（1）由于平面⊥平面，⊥，所以⊥平面，所以⊥，‎ 而，所以四边形是菱形，因此⊥，所以⊥平面．‎ ‎（2）设，作⊥于，连接，‎ 由（1）知⊥平面，即⊥平面，所以⊥，‎ 又⊥于，因此⊥，‎ 所以为两平面所成锐二面角的平面角，‎ 在中，，，故直角边，‎ 又因为中，因此中斜边，‎ 所以，‎ 所以所求两平面所成锐二面角的余弦值为．‎ ‎21.‎ 证明：（1）如图，连接，交于点，连结.‎ 据直三棱柱性质知四边形为平行四边形，所以为的中点.‎ 又因为是的中点，所以.………………2分 又因为平面，平面，‎ 所以平面.………………4分 ‎（2）因为，为的中点，所以.………………5分 据直三棱柱性质知平面，又因为平面，所以 ‎.‎ 又因为，平面，‎ 所以平面，………………11分 又因为平面，所以，即.………………12分 ‎22. ‎ ‎(1)在四边形中，∵// ， ， ，‎ ‎∴四边形是正方形，得.‎ 在中，∵，∴，又, ∴平面,‎ 又平面，∴平面平面.‎ ‎(2)由(1)知，四边形为正方形，∴， ，‎ ‎∴，从而,‎ 设点到平面的距离为，∵平行线与之间的距离为，‎ ‎∴.‎