数学理卷·2017届宁夏银川九中高三上学期第四次月考（2016

数学理卷·2017届宁夏银川九中高三上学期第四次月考（2016

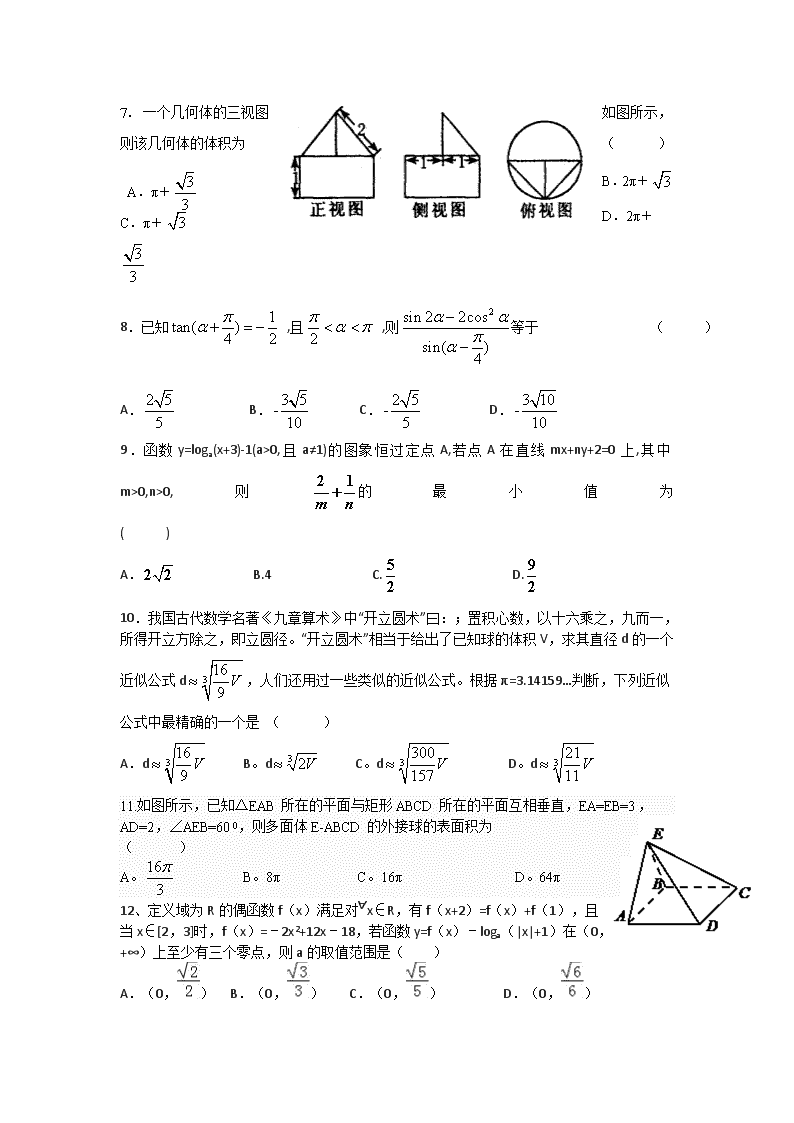
银川九中2016-2017学年度第一学期第四次月考试卷 高三年级数学（理科）试卷 （本试卷满分150分） 命题人：高国君 本试卷分第I卷（选择题）和第II卷（非选择题）两部分，其中第II卷第（22）—（23）题为选考题，其它题为必考题。考生作答时，将答案答在答题卡上，在本试卷上答题无效。‎ 注意事项：‎ ‎1、答题前，考生务必将自己的姓名、学生、班级填写在答题卡上，否则该卷记零分。‎ ‎2、选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净，再选涂其它答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。‎ ‎3、请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。‎ ‎4、保持卡面清洁，不折叠，不破损。‎ ‎5、做选考题时，考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的题号涂黑。‎ 第Ⅰ卷（选择题）‎ 一、选择题：本大题共12题，每小题5分，在每小题给出的四个选项中 ，只有一项是符合题目要求的。‎ ‎1．若全集U=R，集合M={x|﹣x2﹣x+2＜0}，N={x|x﹣1＜0}，则如图中阴影部分表示的集合是 ‎ ‎（　　）‎ A．（﹣∞，1]        B．（1，+∞）      C．（﹣∞，﹣2）     D．（﹣2，1）‎ ‎2．已知复数的实部为﹣1，则复数z﹣b在复平面上对应的点在（　 　）‎ A．第一象限        B．第二象限         C．第三象限             D．第四象限 ‎3．设是两条不同直线，是两个平面，则的一个充分条件是 （ ）‎ A． B． ‎ C． D．‎ ‎4.右图是计算的值算法框图，其中在判断框中应填入的条 件是   （    ）‎ ‎   A．i<8   B．i<9     C．i<10     D．i<11‎ ‎5．已知A，B，C三点不在同一条直线上，O是平面ABC内一定点，P是△ABC内的一动点，若=λ（ + ），λ∈[0，+∞），则直线AP一定过△ABC的 （　　 ）‎ A．重心              B．垂心              C．外心              D．内心 ‎6．等差数列{an}的前n项和为Sn,且满足2S5-13a4+5a8=10，则下列数中恒为常数的是 ( )‎ A.a8 B. S9 C. a17 D. S17‎ ‎7．一个几何体的三视图如图所示，则该几何体的体积为 （ ）‎ ‎ A．π＋ B．2π＋ C．π＋ D．2π＋‎ ‎8．已知 ,且 ,则等于 （　 　 ）‎ A．               B．               C．               D．‎ ‎9．函数y=loga(x+3)-1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+2=0上,其中m>0,n>0,则的最小值为 (　　 )‎ A． B.4 C. D. ‎ ‎10．我国古代数学名著《九章算术》中“开立圆术”曰：；置积心数，以十六乘之，九而一，所得开立方除之，即立圆径。“开立圆术”相当于给出了已知球的体积V，求其直径d的一个近似公式d，人们还用过一些类似的近似公式。根据π=3.14159…判断，下列近似公式中最精确的一个是 （ ）‎ A．d B。d C。d D。d ‎ ‎11.如图所示，已知△EAB所在的平面与矩形ABCD所在的平面互相垂直，EA=EB=3，AD=2，∠AEB=600，则多面体E-ABCD的外接球的表面积为 （     ）‎ A。          B。8π C。16π           D。64π ‎12、定义域为R的偶函数f（x）满足对∀x∈R，有f（x+2）=f（x）+f（1），且当x∈[2，3]时，f（x）=﹣2x2+12x﹣18，若函数y=f（x）﹣loga（|x|+1）在（0，+∞）上至少有三个零点，则a的取值范围是（　　）‎ A．（0，）     B．（0，）        C．（0，）         D．（0，）‎ 第Ⅱ卷（非选择题）‎ 本卷包括必考题和选考题两部分。第（13题）~第（21）题为必考题，每个试题考生都必须做答。第（22题）~第（23）题为选考题，考生根据要求做答。‎ 二．填空题：本大题共4小题，每小题5分，共20分。把答案填写在答题卡上相应位置的横线上.‎ ‎13．在Rt△ABC中，∠A=90°，AB=AC=2，点D为AC中点，点E满足，则=　　．‎ ‎14．某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg，乙材料1 kg，用5个工时；生产一件产品B需要甲材料0.5 kg，乙材料0.3 kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元.该企业现有甲材料150 kg，乙材料90 kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为             元.‎ ‎15．给出下列四个命题：①函数f(x)=3的图象为C. 由f(x)=3sin2x的图象向右平移个单位长度可以得到图象C.②曲线y=在点(4,e2)处的切线与坐标轴所围三角形的面积为e2 ;③已知函数f(x) 满足对任意的实数x1≠x2都有成立,则实数a的取值范围为(0,).以上三个论断中正确的序号为 ‎ ‎16．已知函数f(x)=，数列{an}的通项公式为an=，则此数列前2016项的和为______．‎ 三、解答题：本大题共6小题，共70分。解答题应写出文字说明，证明过程或演算步骤。解答过程写在答题卡的相应位置。‎ ‎17．设函数f(x)=2sinxcosxcos+cos2xsin(-π<<0),y=f(x)图像的一条对称轴方程是直线.‎ ‎（1）求并用“五点法”画出函数y=f(x)在区间[0, π]上的图像； ‎ ‎（2）求函数y=f(x)的单调增区间；‎ x y ‎ ‎ ‎18.△ABC中，角A、B、C的对边分别为a、b、c，且cosC=．（1）求角B的大小；‎ ‎（2）若BD为AC边上的中线，cosA=，BD=，求△ABC的面积．‎ ‎19. 已知数列{an}是等比数列，首项a1=1，公比q＞0，其前n项和为Sn，且S1+a1，S3+a3，S2+a2成等差数列．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）若数列{bn}满足an+1= ，Tn为数列{bn}的前n项和，若Tn≥m恒成立，求m的最大值．‎ ‎20. 如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D、E分别为AB、AC中点．（1）求证：DE∥平面PBC；（2）求证：AB⊥PE；‎ ‎（3）求二面角A﹣PB﹣E的大小 ‎21. 已知函数f（x）=x2﹣（a+2）x+alnx，其中常数a＞0．‎ ‎（Ⅰ）当a=1时，求f(x)的极值。‎ ‎（Ⅱ）当a＞2时，求函数f（x）的单调递增区间；‎ ‎（III））设定义在D上的函数y=h（x）在点P（x0，h（x0））处的切线方程为l：y=g（x），若＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”．当a=4时，试问y=f（x）是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标；若不存在，请说明理由．‎ 请考生在第（22）、（23）二题中任选一题作答，如果多做，则按所做的第一题记分。作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。‎ ‎（22）（本小题满分10分）选修4—4：坐标系与参数方程。‎ ‎22.已知直线的参数方程为为参数，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，且曲线的左焦点在直线上．‎ ‎（Ⅰ）若直线与曲线交于两点，求的值；‎ ‎（Ⅱ）设曲线的内接矩形的周长为，求的最大值．‎ ‎23.（本小题满分10分）选修4-5：不等式选讲 已知函数.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）证明：.‎ 答案：‎ 一． 选择题：‎ BBCCA，DACDD，CB 二、填空题：‎ ‎13．-2 14、216000 15.② 16.2016‎ 三、解答题：‎ ‎17、（1）的图像的对称轴，‎ ‎   ‎ 由 ‎0‎ x ‎0‎ y ‎－1‎ ‎0‎ ‎1‎ ‎0‎ 故函数 ‎18、（1），由正弦定理，得 ‎，‎ ‎  …………………3分 又∵，∴．…………5分 ‎（2）在中，由余弦定理得，∴…①，…8分 在中，由正弦定理得，由已知得.‎ ‎∴，∴……②，‎ 由①，②解得，………………10分∴．……………12分 ‎19、解答： 解：（Ⅰ）法一：由题意可知：2（S3+a3）=（S1+a1）+（S2+a2）‎ ‎∴S3﹣S1+S3﹣S2=a1+a2﹣2a3，即4a3=a1，于是，∵q＞0，∴； ∵a1=1，∴．‎ ‎（Ⅰ）法二：由题意可知：2（S3+a3）=（S1+a1）+（S2+a2）‎ 当q=1时，不符合题意；‎ 当q≠1时，，‎ ‎∴2（1+q+q2+q2）=2+1+q+q，∴4q2=1，∴，‎ ‎∵q＞0，∴，∵a1=1，∴．‎ ‎（Ⅱ）∵，∴，∴，‎ ‎∴（1）‎ ‎∴（2）‎ ‎∴（1）﹣（2）得=∴‎ ‎∵Tn≥m恒成立，只需（Tn）min≥m∵‎ ‎∴{Tn}为递增数列，∴当n=1时，（Tn）min=1，∴m≤1，∴m的最大值为1．‎ ‎20、【解答】解：（Ⅰ）∵D、E分别为AB、AC中点，∴DE∥BC．‎ ‎∵DE⊄平面PBC，BC⊂平面PBC，∴DE∥平面PBC．…‎ ‎（Ⅱ）连接PD，∵PA=PB，D为AB中点，∴PD⊥AB．∵DE∥BC，BC⊥AB，∴DE⊥AB…又∵PD∩DE=D，PD，DE⊂平面PDE∴AB⊥平面PDE…∵PE⊂平面PDE，∴AB⊥PE…‎ ‎（Ⅲ）∵AB⊥平面PDE，DE⊥AB…‎ 如图，以D为原点建立空间直角坐标系，由PA=PB=AB=2，BC=3，‎ 则B（1，0，0），P（0，0，），E（0，，0），∴=（1，0，），=（0，，）．‎ 设平面PBE的法向量，∴‎ 令得…∵DE⊥平面PAB，‎ ‎∴平面PAB的法向量为．…‎ 设二面角的A﹣PB﹣E大小为θ，‎ 由图知，，‎ 所以θ=60°，即二面角的A﹣PB﹣E大小为60°…‎ ‎21、【解答】解：（Ⅰ）函数f（x）的定义域为（0，+∞），∵，‎ ‎∴…∵a＞2，∴，‎ 令f′（x）＞0，即，∵x＞0，∴0＜x＜1或，…‎ 所以函数f（x）的单调递增区间是（0，1），…‎ ‎（Ⅱ）解法一：当a=4时，‎ 所以在点P处的切线方程…‎ 若函数存在“类对称点”P（x0，f（x0）），‎ 则等价于当0＜x＜x0时，f（x）＜g（x），当x＞x0时，f（x）＞g（x）恒成立．…‎ ‎①当0＜x＜x0时，f（x）＜g（x）恒成立，‎ 等价于恒成立，‎ 即当0＜x＜x0时，恒成立，‎ 令，则φ（x0）=0，…‎ 要使φ（x0）＜0在0＜x＜x0恒成立，只要φ（x）在（0，x0）单调递增即可．‎ 又∵，…‎ ‎∴，即．…‎ ‎②当x＞x0时，f（x）＞g（x）恒成立时，．…∴．…‎ 所以y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．…‎ ‎（Ⅱ）解法二：猜想y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．…下面加以证明：‎ 当时，…‎ ‎①当时，f（x）＜g（x）恒成立，‎ 等价于恒成立，‎ 令…‎ ‎∵，∴函数φ（x）在上单调递增，‎ 从而当时，恒成立，‎ 即当时，f（x）＜g（x）恒成立．…‎ ‎②同理当时，f（x）＞g（x）恒成立．…‎ 综上知y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．…‎ ‎22、‎ ‎23、【解析】试题解析： （1）当时，，原不等式等价于 或或 解得：或或.‎ 不等式的解集为.‎