- 2021-06-21 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
内蒙古呼伦贝尔市牙克石林业一中2012届高三数学第四次模拟考试试题 文
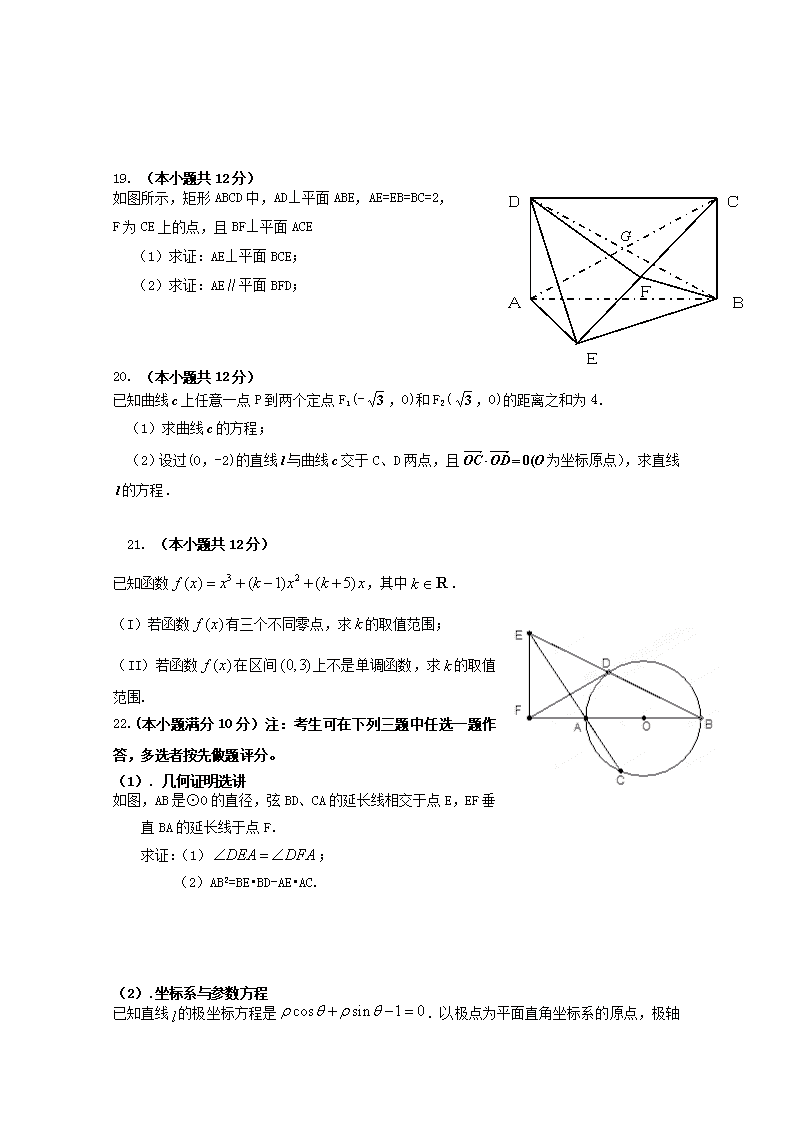
内蒙古呼伦贝尔市牙克石林业一中2012届高三数学第四次模拟考试试题 文 一.选择题(125分=60分) 1.复数,,则在复平面内对应点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.设集合,,则集合等于( ) A. B. C. D. 3.渐近线是和且过点,则双曲线的标准方程是( ) A. B. C.D. 侧视图 正视图 俯视图 4.某简单几何体的三视图如图所示,其正视图.侧视图.俯视图均为直角三角形,面积分别是,,,则这个几何体的体积为( ) A. B. C. D. 5. 幂函数的图象经过点( ) A. B. C. D. 6. 已知向量,,且,则的值为( ) A. B. C. D. 7. 按如图所示的程序框图运算,若输出,则输入的的取值范围是 A., B.(6,19 C., D.(6,19) 8.设表示与中的较大者,则的最小值为 A.0 B.2 C. D.不存在 9. ,下列结论中正确的是( ) A. 函数为偶函数 B.函数最小正周期为 C. 函数的图象关于原点对称 D.函数的最大值为 10.有两个等差数列、,若,则 A. B. C. D. 11. 已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则甲、乙两人得分的中位数之和是( ) A.62 B.63 C.64 D.65 12. 若关于的不等式有实数解,则实数的取值范围为( ) A. B. C. D. 二.填空题(45分=20分) 13. 双曲线的渐近线方程为_______. 14.已知点P(x,y)的坐标满足条件,那么的最大值等于 15. 某工厂生产A、B、C三种不同型号的产品.产品数量之比依次为2∶3∶5,现用分层抽样方法抽出一个容量为n的样本,已知A种型号产品共抽取了16件,那么此样本的容量n= . 16.函数的图像如图,为函数的导函数,则不等式 的解集为 。 x O y 三.解答题(共70分) 17. (本小题共12分) 设函数的最大值为,最小正周期为. (Ⅰ)求、; (16题) (Ⅱ)若有10个互不相等的正数满足 求的值. 18. (本小题共12分) 将一颗骰子先后抛掷2次,观察向上的点数,求: (1)两数之和为5的概率; (2)两数中至少有一个奇数的概率; (3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率. B A D C F E 19. (本小题共12分) 如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2, F为CE上的点,且BF⊥平面ACE (1)求证:AE⊥平面BCE; (2)求证:AE∥平面BFD; 20. (本小题共12分) 已知曲线上任意一点P到两个定点F1(-,0)和F2(,0)的距离之和为4. (1)求曲线的方程; (2)设过(0,-2)的直线与曲线交于C、D两点,且为坐标原点),求直线的方程. 21. (本小题共12分) 已知函数,其中. (I)若函数有三个不同零点,求的取值范围; (II)若函数在区间上不是单调函数,求的取值范围. 22.(本小题满分10分)注:考生可在下列三题中任选一题作答,多选者按先做题评分。 (1). 几何证明选讲 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F. 求证:(1); (2)AB2=BE•BD-AE•AC. (2).坐标系与参数方程 已知直线的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线上求一点,使它到直线的距离最小,并求出该点坐标和最小距离. (3).不等式选讲 已知均为正实数,且. 求的最大值. 牙克石林业一中2011---2012学年高三年级第四次模拟考试 数学试卷(文)参考答案 命题时间:2012.2 命题人:陈海忠 一.选择题(125分=60分) 二.填空题(45分=20分) 13. 14. 15. 80 16. 三.解答题(共70分) 18. 解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件 1分 (1)记“两数之和为5”为事件A,则事件A中含有4个基本事件, 所以P(A)=; 答:两数之和为5的概率为. 4分 (2)记“两数中至少有一个奇数”为事件B,则事件B与“两数均为偶数”为对立事件,所以P(B)=; 答:两数中至少有一个奇数的概率. 8分 (3)基本事件总数为36,点(x,y)在圆x2+y2=15的内部记为事件C,则C包含8个事件,所以P(C)=. 答:点(x,y)在圆x2+y2=15的内部的概率. 12分 19. 解:(1)证明:∵平面,, ∴平面,则 ----------------3分 又平面,则 平面 ----------------6分 (2)由题意可得是的中点,连接 平面,则, 而,是中点 ---------9分 在中,,平面 --12分 20. 解:(1)根据椭圆的定义,可知动点的轨迹为椭圆, ……………………1分 其中,,则. ……………………………2分 所以动点M的轨迹方程为.……………………………………4分 (2)当直线的斜率不存在时,不满足题意.………………………………5分 当直线的斜率存在时,设直线的方程为,设,,∵,∴.………………6分 ∵,, ∴. ∴ .………… ① ……………7分 由方程组得. 则,,………………………………9分 代入①,得. 即,解得,或.…………………………………11分 所以,直线的方程是或.…………………12分 21. 解: (I)因为,所以函数有三个不同零点的充要条件是关于的方程有两个不相等的非零实根,…………1分 即,且. 故的取值范围是…………5分 (II)解法一:,函数在区间上不是单调函数 的充要条件是关于的方程有两个不相等的实数根,且至少有一个实数根在区间内. …………7分 (2) 若,则. 方程的两个实根均不在区间内,所以…………8分 (3) 若,则. 方程在区间内有实根,所以可以为…………9分 (4) 若方程有一个实根在区间内,另一个实根在区间外, 则,即…………10分 (5) 若方程在区间内有两个不相等的实根,则 ………11分 综合①②③④得的取值范围是…………12分 (II)解法二:, 函数在区间上不是单调函数的充要条件是关于的方程 在区间上有实根且…………7分 关于的方程在区间上有实根的充要条件是 使得…………8分 使得 令有,记 …………10分 则函数在上单调递减,在上单调递增,所以有 即.…………11分 又由 得且 故的取值范围是…………12分 (II)解法三:记函数在区间上的最大值为, 最小值为 函数f(x)在区间上不单调函数f(x)在区间上不单调 …………7分 因为函数的图像是开口向上、对称轴为的抛物线, 所以, …………9分 当时,, ……11分 故的取值范围是……12分 (3)解:由柯西不等式得 … 当且仅当a=b=c=时等号成立 故的最大值为.…查看更多