四川省成都高新区2013届高三12月统一检测数学（理）试题

四川省成都高新区2013届高三12月统一检测数学（理）试题

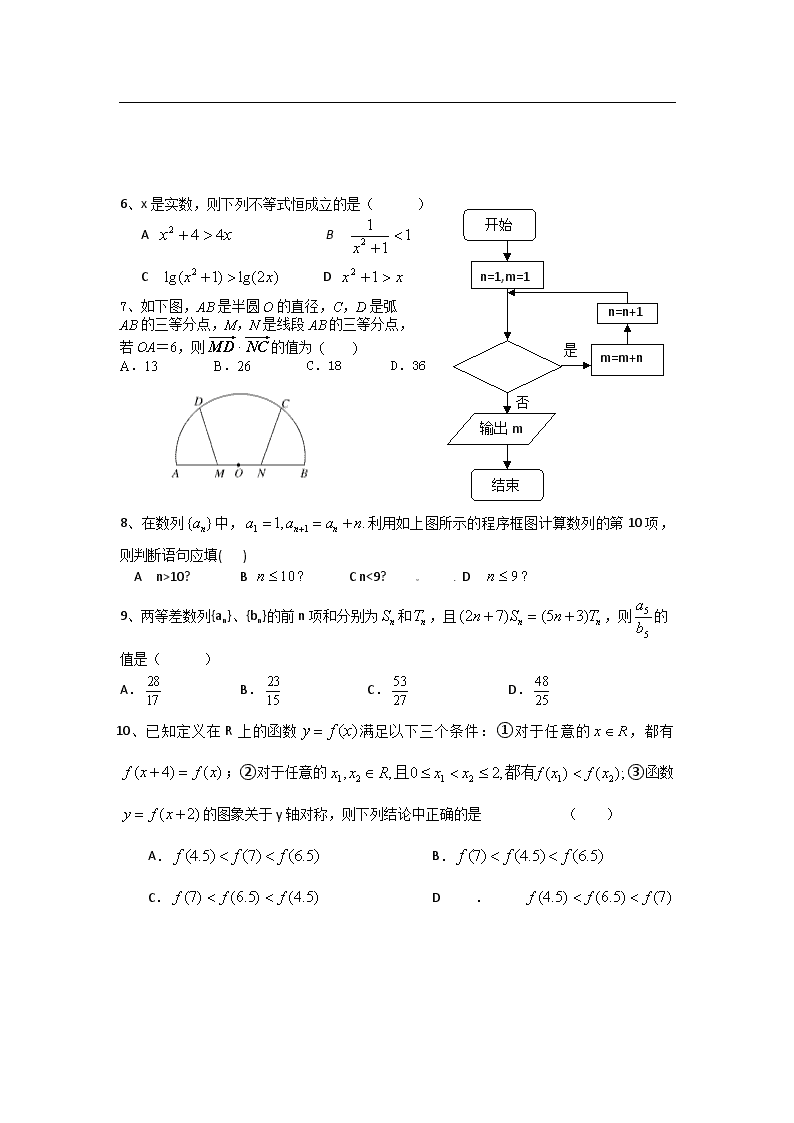
‎2012年高2013届成都高新区12月学月统一检测 数学（理）‎ ‎（考试时间： 月 日 总分：150分）‎ 第Ⅰ卷（选择题，共 50 分）‎ 一．选择题：本大题共10小题，每小题5分，满分50分。在每小题给出的四个选项中。只有一项是符合题目要求的。‎ ‎1．为虚数单位，则=（ ）‎ A - B ‎-1 C D 1‎ ‎2、已知集合，,若，则实数a的取值范围是（）‎ A [2,3] B (2,3) C D ‎ ‎3、如图,非零向量=,=b,且，C为垂足，设向量a,则的值为（ ）‎ A B C D ‎ ‎4、已知等比数列的前三项依次为，，，则（ ）‎ A． B． C． D．‎ ‎5、 设l、m、n表示三条直线，α、β、r表示三个平面，则下面命题中不成立的是（ ）‎ A．若l⊥α，m⊥α，则l∥m B．若mβ，n是l在β内的射影，m⊥l，则m⊥n C．若mα，nα，m∥n，则n∥α D．若α⊥r，β⊥r，则α∥β 开始 n=1,m=1‎ n=n+1‎ m=m+n 是 否 输出m 结束 ‎6、x是实数，则下列不等式恒成立的是（ ）‎ A B ‎ C D ‎ ‎7、如下图，AB是半圆O的直径，C，D是弧 AB的三等分点，M，N是线段AB的三等分点，‎ 若OA＝6，则·的值为 (　　)‎ A．13 B．‎26 ‎‎ C．18 D．36‎ ‎8、在数列中，利用如上图所示的程序框图计算数列的第10项，则判断语句应填( )‎ A n>10? B C n<9? D ‎ ‎9、两等差数列{an}、{bn}的前n项和分别为和，且，则的值是（ ）‎ A． B． C． D．‎ ‎10、已知定义在R上的函数满足以下三个条件：①对于任意的，都有；②对于任意的③函数的图象关于y轴对称，则下列结论中正确的是 （ ）‎ ‎ A． B．‎ ‎ C． D．‎ ‎2012年高2013届成都高新区学月统一检测 数学（理）‎ ‎（考试时间： 月 日 总分：150分）‎ ‎ 第Ⅱ卷（非选择题，共 100 分）‎ 二．填空题：（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）‎ ‎11、某地奥运火炬接力传递路线共分6段，传递活动分别由6名火炬手完成．如果第一棒火炬手只能从甲、乙、丙三人中产生，最后一棒火炬手只能从甲、乙两人中产生，则不同的传递方案共有 种．（用数字作答）．‎ ‎12、已知变量满足下列条件，则的取值范围是___________‎ ‎13、f (x)＝A sin(ωx＋)(A>0, ω>0)的部分图像如图，‎ 则f (1) ＋f (2)＋…＋f (11)＝ .‎ ‎14、设非空集合满足：当时，有. 给出如下三个命题：①若，则；②若，则；③若，则；④若，则或.其中正确命题的是 .‎ ‎15、请考生在下列两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎(1)极坐标系中，曲线和直线交于A、B两点,则线段AB的长= .‎ ‎(2)已知函数，则的取值范围是_______________.‎ 三．解答题：本大题共6小题，共74分，解答应写出文字说明，演算步骤或证明过程。‎ ‎16、在中，角所对的边分别是，满足 ‎（1）求角；‎ ‎（2）若，求面积的最大值。‎ ‎17、为防止风沙危害，某地决定建设防护绿化带，种植杨树、沙柳等植物．甲一次种植了4株沙柳，根据以往的经验，这个人种植沙柳时每种植3株就有2株成活，且各株沙柳成活与否是相互独立的． （Ⅰ ‎）写出成活沙柳的株数的分布列，并求其期望值； （Ⅱ）为了有效地防止风沙危害，该地至少需要种植24000株成活沙柳．如果参加种植沙柳的人每人种植4株沙柳，且参加种植的人都和甲的种植水平一样，问至少需要多少人来参加种植沙柳，才能保证有效防止风沙危害．‎ ‎18、已知数列是公差为2的等差数列,且,,成等比数列.‎ ‎(1)求的通项公式；‎ ‎（2）令 ,记数列的前项和为,求证：.‎ ‎19、如图，在梯形中，，，四边形为矩形，平面平面，.‎ ‎（1）求证：平面；‎ ‎（2）点在线段上运动，设平面与平面所成二面角的平面角为，试求的取值范围.‎ ‎20．（本小题满分13分）‎ 已知函数，，其中．‎ ‎（1）若在其定义域内是单调函数，求实数的取值范围；‎ ‎（2）若（1，），问是否存在，使成立？若存在，求出符合条件的一个；否则，说明理由．‎ ‎21已知函数，满足：‎ ‎①对任意，都有 ‎②对任意都有 ‎（Ⅰ）试证明：为上的单调增函数； [来源:学。科。网Z。X。X。K]‎ ‎（II）求 ‎（III）令，试证明：[来源:学.科.网Z.X.X.K]‎ ‎2012年高2013届成都高新区学月统一检测 数学（理）‎ ‎（考试时间： 月 日 总分： 分）‎ 一、 选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 选项 二、 填空题 ‎11.____________________ 12.__________________ ‎ ‎13. ___________________ 14.____________________ ‎ ‎15.（1）______________ （2）_______________ ‎ 三、 解答题 ‎16.‎ ‎17.‎ ‎[来源:学+科+网]‎ ‎18.‎ ‎19‎ ‎20‎ ‎[来源:Z。xx。k.Com][来源:学。科。网Z。X。X。K]‎ ‎21‎ ‎2012年高2013届成都高新区12月学月统一检测 数学（理）答案 一、选择题 ‎ A B A C D D B D D A ‎ 二、填空题 ‎11. 96‎ ‎12．‎ ‎13.‎ ‎14.①②③④‎ ‎15.（1）8 （2）‎ ‎16.解：(1)由已知及正弦定理得，………2分 得，‎ 化简 ………………………………………………4分 即，…………………………6分 ‎(2)由(1)可知 ，则…………………………………8分 ‎ 即 …………………………………10分 ‎ 即 当b=c=3时，S的最大值是.…………………………………………………………12分 ‎17.解：‎ ‎（Ⅰ）设成活沙柳的株数为X，则X=0，1，2，3，4，‎ 且有P(X=k)= ………………………………………（4分） 据题意，每种植3株就有2株成活，所以p=，故成活沙柳的株数X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎∴X的期望值E（X）‎ ‎=………………………………………（6分） （Ⅱ）设参加种植沙柳的人数为x，则这当中的每一个人都种植了4株沙柳．  据（Ⅰ）的结果，这些人每人都能种植成活的沙柳株，因此，共种植成活的沙柳x株．…………………………………………………………………………………………（9分） 据题意，需x≥24000，解得x≥9000． ‎ 所以，估计至少需要9000人来参加种植沙柳，才能保证有效防止风沙危害．…………………………………………………………………………………………（12分）‎ ‎18.解：‎ ‎（1）数列是公差为2的等差数列，‎ ‎,,成等比数列，,‎ ‎ 所以由 ………………………………………… 3分 得 解之得,所以,即……………………………6分 ‎（2）由（1）得 ‎………………………9分 ‎ ………………………………………………12分 ‎19.解：‎ ‎（1）证明：在梯形中， ‎ ‎∵ ,，‎ ‎∠＝，∴ ………………………………………………………2分 ‎∴ ‎ ‎∴ ∴　⊥…………………………………………4分 ‎∵ 平面⊥平面,平面∩平面,‎ 平面 ∴ ⊥平面 ……………………………………6分 ‎（2）由（1）可建立分别以直线为的如图所示空间直角坐标 系，令，则，‎ ‎∴ ‎ 设为平面的一个法向量，‎ 由 ，‎ 联立得 ，‎ 取，则，…………………………………………………… 8分 ‎ ∵　是平面的一个法向量 ‎∴ …………………10分 ‎∵ ∴　当时，有最小值，‎ ‎ 当时，有最大值. ‎ ‎ ∴ ……………………………………………………………………12分 ‎20. 解：由 ，得 ………（1分）‎ ‎（1）由题意得：在恒成立或在恒成立 ‎ 若恒成立，则恒成立 又 满足题意 ………………（3分）‎ 若恒成立，则恒成立……………（5分）‎ 综合上述，的取值范围是． …………………………………（6分）‎ ‎（2）令．则问题等价于: 找一个使成立，故只需满足函数的最小值即可，…………………………（8分）‎ 因为……（10分）‎ 而 故当时，递减；当时，递增.‎ 于是，，…………（12分）‎ 与上述要求矛盾，故不存在符合条件的………………………………（12分）21解析:‎ (1) 因为,所以可以得到,也就是 ‎,‎ 不妨设,所以,可以得到,也就是说为上的单调增函数.‎ ‎ (2)由(1)可知,令,则可以得到 ‎,又,所以由不等式可以得到,‎ 又,所以可以得到 ①‎ 接下来要运用迭代的思想:‎ 因为,所以,, ②‎ ‎,,,‎ ‎,又单调递增，，所以可以判断 ③‎ 所以,综合①②③有=‎ ‎(3),‎ 又由（1），所以,‎ 从而,‎ 一方面,‎ 另一方面，所以,‎ 综上有.‎