2017-2018学年山东省淄博市淄川中学高二上学期第一次月考数学（理）试题

2017-2018学年山东省淄博市淄川中学高二上学期第一次月考数学（理）试题

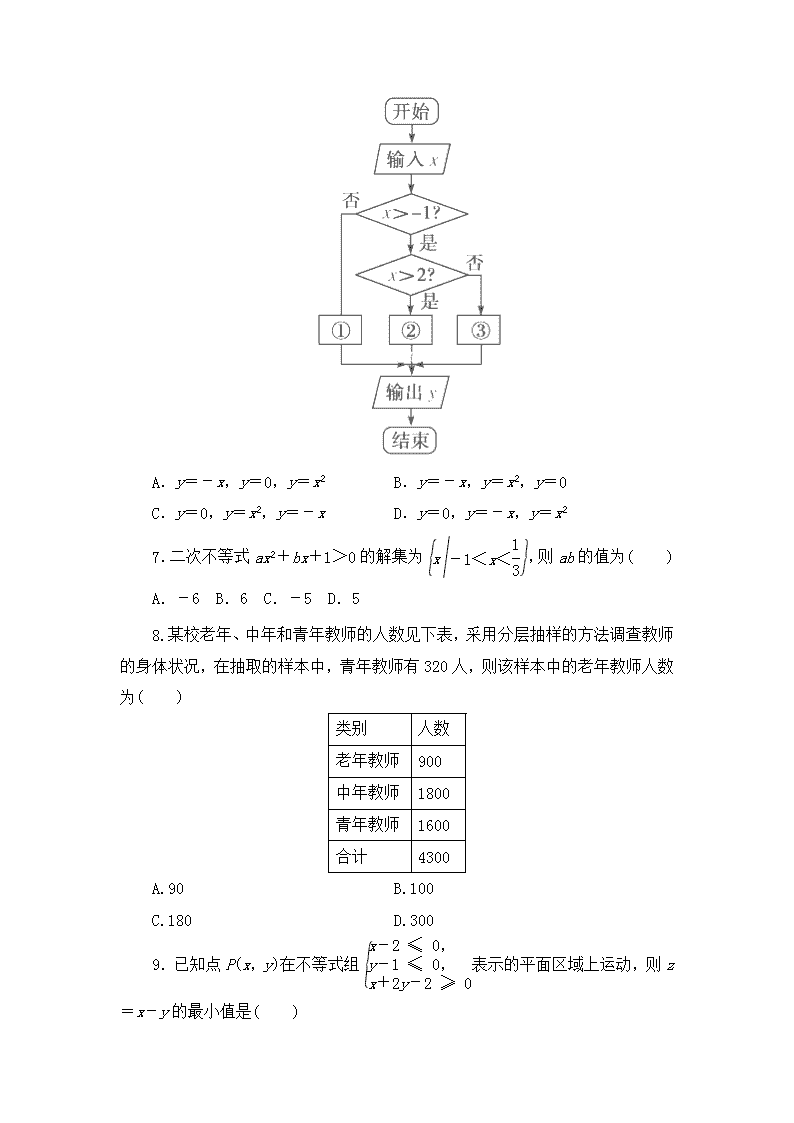
‎2017-2018学年山东省淄博市淄川中学高二上学期第一次月考理科数学试卷 一、选择题（每题5分，共60分）‎ ‎1．不等式x2≥2x的解集是(　　)‎ A．{x|x≥2} B．{x|x≤2}‎ C．{x|0≤x≤2} D．{x|x≤0或x≥2}‎ ‎2．在△ABC中，A＝60°，a＝4，b＝4，则B等于(　　)‎ A．45°或135° B．135°‎ C．45° D．30°‎ ‎3．已知各项均为正数的等比数列{an}，a1·a9＝16，则a2·a5·a8的值为(　　)‎ A．16 B．32 C．48 D．64‎ ‎4．若三条线段的长分别为3、5、7，则用这三条线段(　　)‎ A．能组成直角三角形 B．能组成锐角三角形 C．能组成钝角三角形 D．不能组成三角形 ‎5．一个射手进行射击，记事件E1：“脱靶”，E2：“中靶”，E3：“中靶环数大于‎4”‎，E4：“中靶环数不小于‎5”‎，则在上述事件中，互斥而不对立的事件共有(　　)‎ A．1对　　　　　　　　　 B．2对 C．3对 D．4对 ‎6．如图所示是计算函数y＝的值的程序框图，则在①②③处应分别填入的是(　　)‎ A．y＝－x，y＝0，y＝x2 B．y＝－x，y＝x2，y＝0‎ C．y＝0，y＝x2，y＝－x D．y＝0，y＝－x，y＝x2‎ ‎7．二次不等式ax2＋bx＋1＞0的解集为，则ab的值为(　　)‎ A．－6 B．‎6 C．－5 D．5‎ ‎8.某校老年、中年和青年教师的人数见下表，采用分层抽样的方法调查教师的身体状况，在抽取的样本中，青年教师有320人，则该样本中的老年教师人数为(　　)‎ 类别 人数 老年教师 ‎900‎ 中年教师 ‎1800‎ 青年教师 ‎1600‎ 合计 ‎4300‎ A.90 B.100‎ C.180 D.300‎ ‎9．已知点P(x，y)在不等式组表示的平面区域上运动，则z＝x－y的最小值是(　　)‎ A．－2 B．‎2 C．－1 D．1‎ ‎10．下列函数：‎ ‎①y＝x＋(x≥2)；②y＝tan x＋；③y＝x－3＋.‎ 其中最小值为2的个数有(　　)‎ A．0个 B．1个 C．2个 D．3个 ‎11．在△ABC中，角A，B，C所对的边分别是a，b，c，若acos B＝bcos A，则△ABC是(　　)‎ A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等腰或直角三角形 ‎12．数列1，1＋2，1＋2＋4，…，1＋2＋22＋…＋2n－1，…的前n项和Sn>1 020，那么n的最小值是(　　)‎ A．7 B．8‎ C．9 D．10‎ 二、填空题（每题5分，共20分）‎ ‎13、取一根长度为‎3cm的绳子，拉直后在任意位置剪断，那么两段的长都不小于‎1m的概率是（ ）‎ ‎14．等差数列{an}的前n项和为Sn，若S2＝2，S4＝10，则S6等于(　　)‎ ‎15．已知a＞0，b＞0，a，b的等差中项是，且α＝a＋，β＝b＋.则α＋β的最小值是(　　)‎ ‎16.执行右面的程序框图，如果输入的t=0.01，则输出的n=( )‎ 三、解答题（共70分）‎ ‎17．(10分)在△ABC中，角A、B、C所对边分别为a、b、c，已知a＝2，c＝3，cosB＝.‎ ‎(1)求b的值；‎ ‎(2)求sinC的值．‎ ‎18.( 12分)甲、乙两家商场对同一种商品开展促销活动，对购买该商品的顾客两家商场的奖励方案如下：‎ 甲商场：顾客转动如图所示圆盘，当指针指向阴影部分(图中四个阴影部分均为扇形，且每个扇形圆心角均为15°，边界忽略不计)即为中奖.‎ 乙商场：从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分)，如果摸到的是2个红球，即为中奖.问：购买该商品的顾客在哪家商场中奖的可能性大？‎ ‎19.( 12分)某班同学利用国庆节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：‎ 组数 分组 低碳族的人数 占本组的频率 第一组 ‎[25，30)‎ ‎120‎ ‎0.6‎ 第二组 ‎[30，35)‎ ‎195‎ p 第三组 ‎[35，40)‎ ‎100‎ ‎0.5‎ 第四组 ‎[40，45)‎ a ‎0.4‎ 第五组 ‎[45，50)‎ ‎30‎ ‎0.3‎ 第六组 ‎[50，55]‎ ‎15‎ ‎0.3‎ ‎(1)补全频率分布直方图并求n、a、p的值；‎ ‎(2)从年龄段在[40，50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在[40，45)岁的概率.‎ ‎20．(12分)已知数列{an}是公差为2的等差数列，它的前n项和为Sn，且a1＋1，a3＋1，a7＋1成等比数列．‎ ‎(1)求{an}的通项公式；‎ ‎(2)求数列的前n项和Tn.‎ ‎21．(12分)解关于x的不等式ax2－(a＋1)x＋1＜0.‎ ‎22．(12分)徐州、苏州两地相距500千米，一辆货车从徐州行驶到苏州，规定速度不得超过100千米/时．已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成：可变部分与速度v(千米/时)的平方成正比，比例系数为0.01；固定部分为a元(a＞0)．‎ ‎(1)把全程运输成本y(元)表示为速度v(千米/时)的函数，并指出这个函数的定义域；‎ ‎(2)为了使全程运输成本最小，汽车应以多大速度行驶？‎ 淄川中学高2016级阶段性检测数学答案 一．选择题 DCDCB BBBCCA AD 二．填空题 ‎ 24 5 7‎ 三．解答题 ‎17解析：(1)由余弦定理，b2＝a2＋c2－2accosB，‎ 得b2＝22＋32－2×2×3×＝10，‎ ‎∴b＝.‎ ‎(2)由余弦定理，得 cosC＝＝＝.‎ ‎∵C是△ABC的内角，‎ ‎∴sinC＝＝.‎ ‎18解析：　如果顾客去甲商场，试验的全部结果构成的区域为圆盘的面积πR2，阴影部分的面积为＝，‎ 则在甲商场中奖的概率为P1＝＝；‎ 如果顾客去乙商场，记3个白球为a1，a2，a3，3个红球为b1，b2，b3，记(x，y)为一次摸球的结果，则一切可能的结果有：‎ ‎(a1，a2)，(a1，a3)，(a1，b1)，(a1，b2)，(a1，b3)，(a2，a3)，(a2，b1)，(a2，b2)，(a2，b3)，(a3，b1)，(a3，b2)，(a3，b3)，(b1，b2)，(b1，b3)，(b2，b3)，共15种，‎ 摸到的是2个红球有(b1，b2)，(b1，b3)，(b2，b3)，共3种，‎ 则在乙商场中奖的概率为P2＝＝，‎ 又P1＜P2，则购买该商品的顾客在乙商场中奖的可能性大.‎ ‎19解析：　(1)第二组的频率为1－(0.04＋0.04＋0.03＋0.02＋0.01)×5＝0.3，‎ 所以高为＝0.06.频率直方图如下：‎ 第一组的人数为＝200，频率为0.04×5＝0.2，所以n＝＝1 000.‎ 由题可知，第二组的频率为0.3，所以第二组的人数为1 000×0.3＝300，所以p＝＝0.65.‎ 第四组的频率为0.03×5＝0.15，所以第四组的人数为1 000×0.15＝150，所以a＝150×0.4＝60.‎ ‎(2)因为[40，45)岁年龄段的“低碳族”与[45，50)岁年龄段的“低碳族”的比值为60∶30＝2∶1，所以采用分层抽样法抽取6人，[40，45)岁中有4人，[45，50)岁中有2人.‎ 设[40，45)岁中的4人为a、b、c、d，[45，50)岁中的2人为m、n，则选取2人作为领队的有(a，b)、(a，c)、(a，d)、(a，m)、(a，n)、(b，c)、(b，d)、(b，m)、(b，n)、(c，d)、(c，m)、(c，n)、(d，m)、(d，n)、(m，n)，共15种；其中恰有1人年龄在[40，45)岁的有(a，m)、(a，n)、(b，m)、(b，n)、(c，m)、(c，n)、(d，m)、(d，n)，共8种.‎ 所以选取的2名领队中恰有1人年龄在[40，45)岁的概率为P＝.‎ ‎20解：(1)由题意，得a3＋1＝a1＋5，a7＋1＝a1＋13，‎ 所以由(a3＋1)2＝(a1＋1)·(a7＋1)得(a1＋5)2＝(a1＋1)·(a1＋13)，‎ 解得a1＝3，所以an＝3＋2(n－1)，即an＝2n＋1.‎ ‎(2)由(1)知an＝2n＋1，则 Sn＝n(n＋2)，＝，‎ Tn＝＋＝＝－.‎ ‎21解析：　若a＝0，原不等式可化为－x＋1＜0，‎ 解得x＞1；‎ 若a＜0，原不等式可化为(x－1)＞0‎ 解得x＜或x＞1；‎ 若a＞0，原不等式可化为(x－1)＜0，‎ 其解的情况应由与1的大小关系确定，‎ 当a＝1时，解得x∈∅；‎ 当a＞1时，解得＜x＜1；‎ 当0＜a＜1时，解得1＜x＜.‎ 综上所述，当a＜0时，解集为；‎ 当a＝0时，解集为{x|x＞1}；‎ 当0＜a＜1时，解集为；‎ 当a＝1时，解集为∅；‎ 当a＞1时，解集为.‎ ‎22解：(1)依题意知汽车从甲地匀速行驶到乙地所用时间为，则全程运输成本为 y＝a·＋0.01v2·＝＋5v，‎ 则y＝＋5v, v∈(0，100]．‎ ‎(2)依题意知a，v都为正数，‎ 则＋5v≥2 ＝100，‎ 当且仅当＝‎5a，即v＝10时取等号．‎ 若10≤100，即0＜a≤100，当v＝10时，全程运输成本y 最小．‎ 若10＞100，即a＞100时，则当v∈(0，100]时，可以证明函数y＝＋5v是减函数，即此时当v＝100时，全程运输成本y最小．‎ 综上所得，当0＜a≤100时，行驶速度应为v＝‎10千米/时，全程运输成本最小；‎ 当a＞100时，行驶速度应为v＝‎100千米/时，全程运输成本最小．‎