- 2021-06-20 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2010年高考试题—数学理(山东)
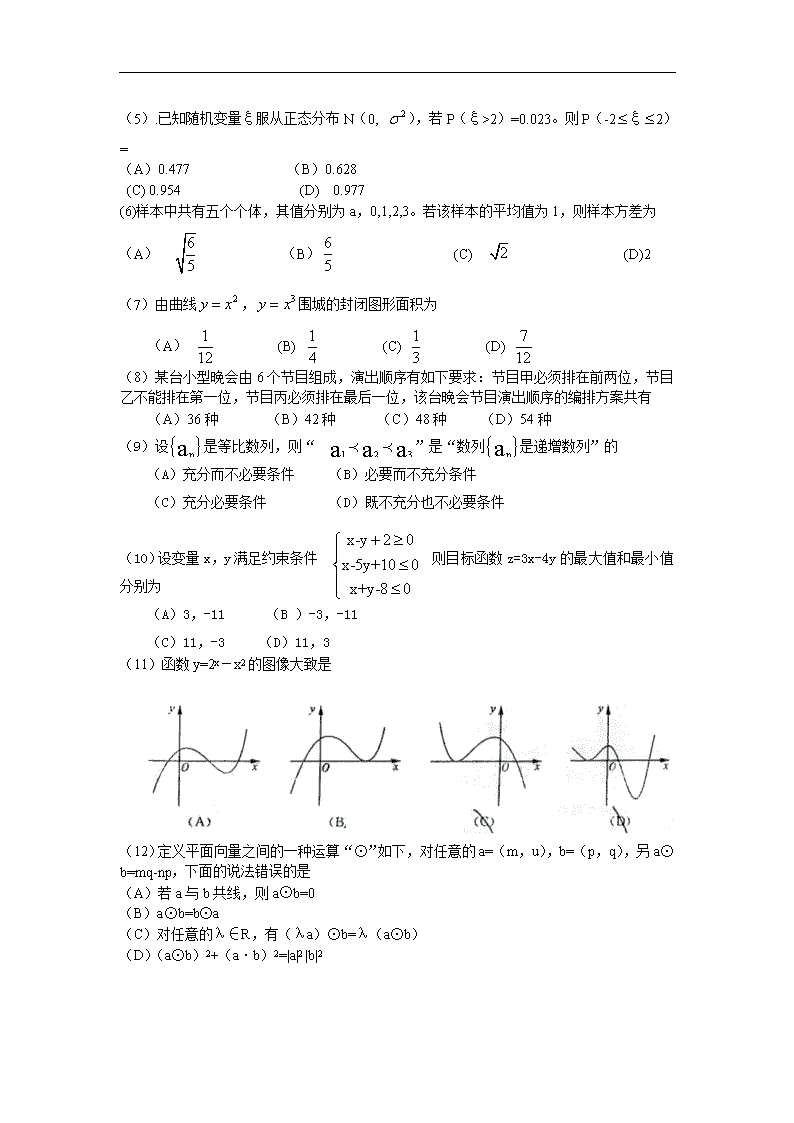
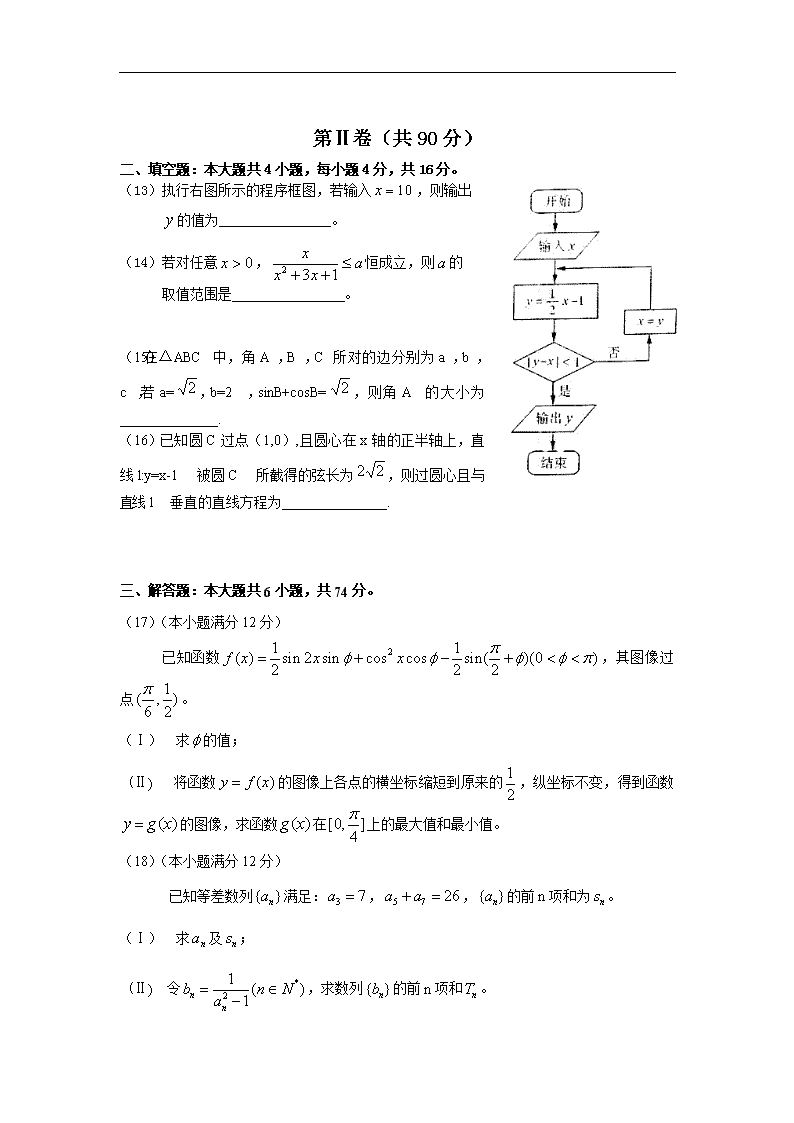
2010年普通高等学校招生全国统一考试(山东卷) 数学理 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分150分,考试用时120分钟,考试结束后将本试卷和答题卡一并交回 注意事项: 答题前,考生务必用0.5毫米黑色签字笔将自已的姓名、准考证号、县区和科类填写在答填写在答题卡和试卷规定的位置上。 2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目上的答案符号涂黑;如需改动,用像皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。 3.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。 4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。 参考公式: 锥体的体积公式:V=Sh,其中S是锥体的底面积,h 是锥体的高。 如果事件A、B互斥,那么P(A+B)=P(A)+P(B):如果事件A、B独立,那么P(AB)=P(A)·P(B)。 (1)已知全集,几何=,则,= (A) (B) (C) (D) (2)已知=(),其中为虚数单位,则 (A) (B)1 (C)2 (D)3 (3)在空间,下列命题正确的是 (A)平行直线的平行投影重合 (B)平行于同一直线的两个平面平行 (C)垂直于同一平面的两个平面平行 (D)垂直于同一平面的两条直线平行 (4)设为定义在R上的奇函数。当x≥0时,=+2x+b(b为常数),则= (A)3 (B)1 (C)-1 (D)-3 (5).已知随机变量ξ服从正态分布N(0, ),若P(ξ>2)=0.023。则P(-2ξ2) = (A)0.477 (B)0.628 (C) 0.954 (D) 0.977 (6)样本中共有五个个体,其值分别为a,0,1,2,3。若该样本的平均值为1,则样本方差为 (A) (B) (C) (D)2 (7)由曲线,围城的封闭图形面积为 (A) (B) (C) (D) (8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有 (A)36种 (B)42种 (C)48种 (D)54种 (9)设是等比数列,则“”是“数列是递增数列”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 (10)设变量x,y满足约束条件则目标函数z=3x-4y的最大值和最小值分别为 (A)3,-11 (B )-3,-11 (C)11,-3 (D)11,3 (11)函数y=2x-x2的图像大致是 (12)定义平面向量之间的一种运算“⊙”如下,对任意的a=(m,u),b=(p,q),另a⊙b=mq-np,下面的说法错误的是 (A)若a与b共线,则a⊙b=0 (B)a⊙b=b⊙a (C)对任意的λ∈R,有(λa)⊙b=λ(a⊙b) (D)(a⊙b)2+(a·b)2=|a|2 |b|2 第Ⅱ卷(共90分) 二、填空题:本大题共4小题,每小题4分,共16分。 (13)执行右图所示的程序框图,若输入,则输出 的值为 。 (14)若对任意,恒成立,则的 取值范围是 。 (15) 在△ABC中,角A,B,C所对的边分别为a,b,c,若a=,b=2,sinB+cosB=,则角A的大小为______________. (16) 已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l:y=x-1被圆C所截得的弦长为,则过圆心且与直线l垂直的直线方程为_______________. 三、解答题:本大题共6小题,共74分。 (17)(本小题满分12分)高考资源网 已知函数,其图像过点。 (Ⅰ) 求的值; (Ⅱ) 将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像,求函数在上的最大值和最小值。 (18)(本小题满分12分) 已知等差数列满足:,,的前n项和为。 (Ⅰ) 求及; (Ⅱ) 令,求数列的前n项和。 (19)(本小题满分12分) 如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45。 。AB=2,BC=2AE=4,三角形PAB是等腰三角形。 (Ⅰ)求证:平面PCD⊥平面PAC; (Ⅱ)求直线PB与平面PCD所成角的大小; (Ⅲ)求四棱锥P—ACDE的体积。 (20)(本小题满分12分) 某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下: ① 每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分; ② 每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局; ③ 每位参加者按问题A、B、C、D顺序作答,直至答题结束。 假设甲同学对问题A、B、C、D回答正确的概率依次为、、、,且各题回答正确与否相互之间没有影响。 (Ⅰ)求甲同学能进入下一轮的概率; (Ⅱ)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。 21.(本小题满分12分) 如图,已知椭圆(a>b>0)的离心率为,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。 (Ⅰ)求椭圆和双曲线的标准方程 (Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1 (Ⅲ)是否存在常数,使得|AB|+|CD|=|AB|·|CD|恒成立?若存在,求的值,若不存在,请说明理由。 (22)(本小题满分14分) 已知函数 (Ⅰ)当a≤时,讨论f(x)的单调性: (Ⅱ)设.当a=时,若对任意x1∈(0,2),存在x2∈,使,求实数b的取值范围。查看更多