2018-2019学年陕西省榆林市第二中学高二下学期第一次月考数学（文）试题（Word版）

2018-2019学年陕西省榆林市第二中学高二下学期第一次月考数学（文）试题（Word版）

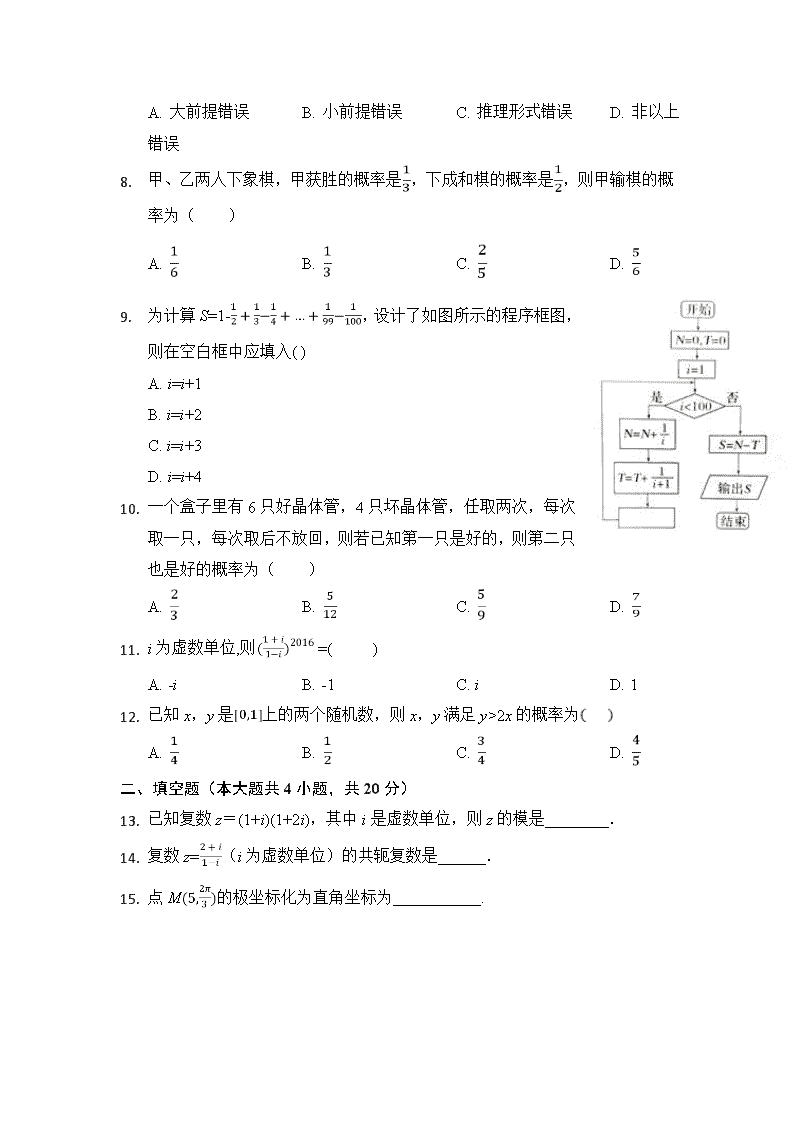
榆林市第二中学2018--2019学年第二学期第一次月考 高二年级数学（文科）试题 命题人： ‎ 时间：120分钟 满分：150分 一、选择题（本大题共12小题，共60分）‎ 1. ‎（1+i）（2+i）=（　　）‎ A. 1-i B. 1+3i C. 3+i D. 3+3i 2. 设复数z满足（1+i）z=2i，则|z|=（　　）‎ A. B. C. D. 2‎ 3. 下列有关样本相关系数的说法不正确的是（　　）‎ A. 相关系数用来衡量x与y之间的线性相关程度 B. |r|≤1，且|r|越接近0，相关程度越小 C. |r|≤1，且|r|越接近1，相关程度越大 D. |r|≥1，且|r|越接近1，相关程度越大 4. 用反证法证明“自然数a，b，c中恰有一个偶数”时，下列假设正确的是（　　）‎ A. 假设a，b，c至少有两个偶数 B. 假设a，b，c都是奇数 C. 假设a，b，c都是奇数或至少有两个偶数 D. 假设a，b，c都是偶数 5. 从2名男同学和3名女同学中任选2人参加社区服务，则选中的2人都是女同学的概率为( )‎ A. 0.6 ‎B. ‎0.5 ‎C. 0.4 D. 0.3‎ 6. 某人在打靶中，连续射击2次，事件“至少有一次中靶”的互斥事件是（　　）‎ A. 至多有一次中靶 B. 两次都中靶 C. 两次都不中靶 D. 只有一次中靶 7. 有一段演绎推理是这样的： “若直线平行于平面，则直线平行于平面内所有直线；已知直线b⊈平面α，直线a⊆平面α，直线b∥平面α，则直线b∥直线a”的结论显然是错误的，这是因为（　　）‎ A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 非以上错误 1. 甲、乙两人下象棋，甲获胜的概率是，下成和棋的概率是，则甲输棋的概率为（　　）‎ A. B. C. D. ‎ 2. 为计算S=1-，设计了如图所示的程序框图，则在空白框中应填入( ) ‎ A. i=i+1 B. i=i+‎2 ‎C. i=i+3 D. i=i+4‎ 3. 一个盒子里有6只好晶体管，4只坏晶体管，任取两次，每次取一只，每次取后不放回，则若已知第一只是好的，则第二只也是好的概率为（　　）‎ A. B. C. D. ‎ 4. i为虚数单位,则​ =( )‎ A. -i B. ‎-1 ‎C. i D. 1‎ 5. 已知x，y是上的两个随机数，则x，y满足y>2x的概率为　　‎ A. B. C. D. ‎ 二、填空题（本大题共4小题，共20分）‎ 6. 已知复数z＝(1+i)(1+2i)，其中i是虚数单位，则z的模是________．‎ 7. 复数z=（i为虚数单位）的共轭复数是______．‎ 8. 点M的极坐标化为直角坐标为___________.‎ 1. 观察下列砌钢管的横截面图： 则第n个图的钢管数是______ ．（用含n的式子表示）‎ 三、解答题（本大题共6小题，共70分）‎ 2. ‎（12分）实数m为何值时，复数z=（m2‎-8m+15）+（m2‎-5m）i是： （1）纯虚数； （2）等于3+6i；‎ ‎18.（12分）如图是某国近7年生活垃圾无害化处理量（单位：亿吨）的折线图． （Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以证明； （Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测第9年该国生活垃圾无害化处理量． 附注： 参考数据：yi=9.32，tiyi=40.17，=0.55，≈2.646． 参考公式：相关系数r=， 回归方程=+t中斜率和截距的最小二乘估计公式分别为： =，=-．‎ ‎ ‎ ‎19.（12分）年级组长徐老师为教育同学们合理使用手机，在本年级内随机抽取了30名同学做问卷调查．经统计，在这30名同学中长时间使用手机的同学恰占总人数的，长时间使用手机且年级名次200名以内的同学有4人，短时间用手机而年级名次在200名以外的同学有2人． （Ⅰ）请根据已知条件完成2×2列联表；‎ 长时间用手机 短时间用手机 总计 名次200以内 名次200以外 总计 ‎（Ⅱ）判断我们是否有99%的把握认为“学习成绩与使用手机时间有关” 【附表及公式】‎ P（K2≥k0）‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎20.（12分）某中学调查了某班全部45名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）‎ 参加书法社团 未参加书法社团 参加演讲社团 ‎8‎ ‎5‎ 未参加演讲社团 ‎2‎ ‎30‎ ‎（Ⅰ）从该班随机选1名同学，求该同学至少参加一个社团的概率； （Ⅱ）在既参加书法社团又参加演讲社团的8名同学中，有5名男同学A1，A2，A3，A4，A5，3名女同学B1，B2，B3．现从这5名男同学和3名女同学中各随机选1人，求A1被选中且B1未被选中的概率． ‎ ‎ ‎ ‎21.（12分）设函数f（x）=5-|x+a|-|x-2|． （1）当a=1时，求不等式f（x）≥0的解集； （2）若f（x）≤1，求a的取值范围． ‎ ‎ ‎ ‎22.（10分）选修4-4：坐标系与参数方程 在平面直角坐标系中，以原点为极点，轴正半轴为极轴建立极坐标系且具有相同的长度单位。‎ ‎ 将下列曲线的极坐标方程化成直角坐标方程，直角坐标方程化成极坐标方程。‎ （1） ‎ 2ρcosθ-ρsinθ=4； （2）. （3）  （4） （5）y2=4x； ‎ ‎ ‎ 高二月考文科 答案和解析 ‎【答案】‎ ‎1. B 2. C 3. D 4. C 5. D 6. C 7. A 8. A 9. B 10. C 11. D 12. A ‎ ‎13.   ‎ ‎14.   ‎ ‎15.  ； .  ‎ ‎16.   ‎ ‎17. 解：（1）由复数z=（m2‎-8m+15）+（m2‎-5m）i是纯虚数， 则m2‎-8m+15=0，且m2‎-5m≠0，解得m=3． （2）由复数z=（m2‎-8m+15）+（m2‎-5m）i=3+6i， 可得：m2‎-8m+15=3，且m2‎-5m=6，解得m=6． （3）由复数z=（m2‎-8m+15）+（m2‎-5m）i所对应的点在第四象限． ∴m2‎-8m+15＞0，m2‎-5m＜0． 解得0＜m＜3．  ‎ ‎18. 解：（1）由折线图看出，y与t之间存在较强的正相关关系，理由如下： ∵r==≈≈≈0.993， ∵0.993＞0.75， 故y与t之间存在较强的正相关关系； （2）==≈≈0.103， =-≈1.331-0.103×4≈0.92， ∴y关于t的回归方程=0.10t+0.92， 故=0.10×9+0.92=1.82， 预测第9年我国生活垃圾无害化处理量为1.82亿吨．  ‎ ‎19. 解：（Ⅰ）根据题意，填写列联表如下；‎ 长时间用手机 短时间用手机 总计 名次200以内 ‎4‎ ‎8‎ ‎12‎ 名次200以外 ‎16‎ ‎2‎ ‎18‎ 总计 ‎20‎ ‎10‎ ‎30‎ ‎（Ⅱ）根据表中数据，计算， 对照临界值P（K2≥6.635）=0.01， 所以，有99%的把握认为“学习成绩与使用手机时间有关”．  ‎ ‎20. 解：（Ⅰ）设“至少参加一个社团”为事件A； 从45名同学中任选一名有45种选法，∴基本事件数为45； 通过列表可知事件A的基本事件数为8+2+5=15； 这是一个古典概型，∴P（A）=； （Ⅱ）从5名男同学中任选一个有5种选法，从3名女同学中任选一名有3种选法； ∴从这5名男同学和3名女同学中各随机选1人的选法有5×3=15，即基本事件总数为15； 设“A1被选中，而B1未被选中”为事件B，显然事件B包含的基本事件数为2； 这是一个古典概型，∴．  ‎ ‎21. 解：（1）当a=1时，f（x）=5-|x+1|-|x-2|=． 当x≤-1时，f（x）=2x+4≥0，解得-2≤x≤-1， 当-1＜x＜2时，f（x）=2≥0恒成立，即-1＜x＜2， 当x≥2时，f（x）=-2x+6≥0，解得2≤x≤3， 综上所述不等式f（x）≥0的解集为[-2，3]， （2）∵f（x）≤1， ∴5-|x+a|-|x-2|≤1， ∴|x+a|+|x-2|≥4， ∴|x+a|+|x-2|=|x+a|+|2-x|≥|x+a+2-x|=|a+2|， ‎ ‎∴|a+2|≥4， 解得a≤-6或a≥2， 故a的取值范围（-∞，-6]∪[2，+∞）．  ‎ ‎22. 本题考查的知识点是参数方程和极坐标，熟练掌握参数方程与普通方程及极坐标方程之间的转化方式，是解答的关键.属中档题.‎ ‎（1）直接利用公式转化即可；‎ ‎（2）直接运用直线参数方程的几何意义即可求解.‎