昆明市第一中学2020届高三摸底考试文科数学第1次——答案

昆明市第一中学2020届高三摸底考试文科数学第1次——答案

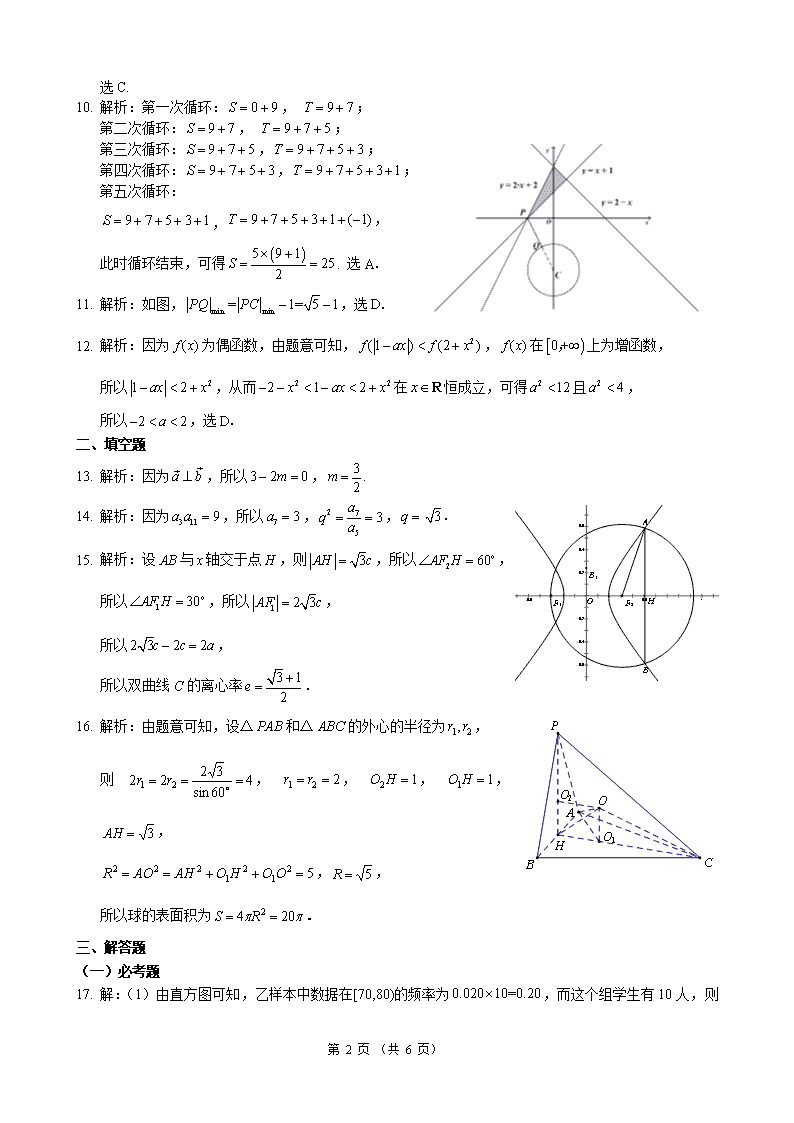
昆明市第一中学2020届摸底考试 参考答案（文科数学）‎ 命题、审题组教师 杨昆华 张宇甜 顾先成 鲁开红 王海泉 莫利琴 吕文芬 张远雄 崔锦 杨耕耘 一、选择题 ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B D C C A B D C A D D 1. 解析：因为，所以，选B.‎ 2. 解析：，选B.‎ 3. 解析：记3名同学及他们所写贺卡分别为，则他们拿到的贺卡的排列方式分别为，，，，，，共6种，其中对应位置字母都不同的有，，共2种，则所求概率，选D．‎ 4. 解析：因为用分层抽样的方法从某校学生中抽取一个容量为45的样本，其中高三年级抽12人,高二年级抽16人，所以高一年级要抽取45-12-16=17人，因为该校高中学共有2700名学生，所以各年级抽取的比例是，所以该校高一年级学生人数为人，选C.‎ 5. 解析：因为，，所以，所以，选C．‎ 6. 解析：因为（），所以，‎ 所以，所以在上的最大值为，选A．‎ 7. 解析：因为，所以，，选，选B.‎ 8. 解析：连结，，则为的中点，所以∥，‎ 因为，，，所以平面，‎ 所以平面，选D．‎ 9. 解析：由得，又，则，‎ 若，则，此时，是的一个极大值点，舍去；‎ 若，则，此时，是的一个极小值点，满足题意，故，‎ 第 6 页 （共 6 页）‎ 选C.‎ 1. 解析：第一次循环：， ；‎ 第二次循环：， ；‎ 第三次循环：，；‎ 第四次循环：，；‎ 第五次循环：‎ ‎，，‎ 此时循环结束，可得. 选A.‎ 2. 解析：如图，，选D.‎ 3. 解析：因为为偶函数，由题意可知，，在上为增函数，‎ 所以，从而在恒成立，可得且，‎ 所以，选D.‎ 二、填空题 4. 解析：因为，所以，.‎ 5. 解析：因为，所以，，.‎ 6. 解析：设与轴交于点，则，所以，‎ 所以，所以，‎ 所以，‎ 所以双曲线的离心率．‎ 7. 解析：由题意可知，设△和△的外心的半径为，‎ 则，，，，，‎ ‎，，‎ 所以球的表面积为.‎ 三、解答题 ‎（一）必考题 8. 解：（1）由直方图可知，乙样本中数据在[70,80)的频率为，而这个组学生有10人，则，得 第 6 页 （共 6 页）‎ ‎． ………2分 由乙样本数据直方图可知，‎ 故． ………4分 ‎（2） 甲样本数据的平均值估计值为 ‎． ………7分 由（1）知，故乙样本数据直方图中前三组的频率之和为，‎ 前四组的频率之和为，‎ 故乙样本数据的中位数在第4组，则可设该中位数为，‎ 由得 ‎，故乙样本数据的中位数为． ‎ 根据样本估计总体的思想，可以估计该校理科班学生本次模拟测试数学成绩的平均值约为，文科班学生本次模拟测试数学成绩的中位数约为． ………12分 1. 解：（1）因为，所以，‎ ‎，可得. ………6分 ‎（2）因为是角平分线，所以，‎ 由，可得，，‎ 所以，‎ 由可得. ………12分 19. ‎（1）证明：因为正方形中，∥，梯形中，∥，所以∥，‎ 所以四点共面； ‎ 因为，所以，因为，，‎ 所以平面，‎ 因为平面，所以， ‎ 在直角梯形中，，，，可求得，‎ 同理在直角梯形中，可求得，又因为，‎ 则，由勾股定理逆定理可知，‎ 因为，，所以平面，‎ 因为平面，故平面平面，即平面平面. ………6分 ‎ 第 6 页 （共 6 页）‎ ‎（2）在等腰直角三角形中，边上的高为，所以点到平面的距离等于，‎ 因为与平面平行，所以点到平面的距离，‎ 三角形的面积，‎ ‎△中，边上的高为， ‎ 又因为△的面积， ‎ 设点到平面的距离为，由三棱锥的体积,‎ 得，故点到平面的距离为. ………12分 19. 解：（1）设，，直线，‎ 所以得，所以，‎ 由，所以，‎ 即，‎ 同理，联立得，‎ 即． ………6分 ‎（2）因为，，‎ 所以，‎ ‎，即，‎ ‎，‎ 同理，‎ ‎，‎ 当且仅当时，四边形面积的最小值为32. ………12分 20. 解：（1）， ‎ 第 6 页 （共 6 页）‎ 令，，‎ 则，则在上单调递增，‎ ‎①.若，则，则，则在上单调递增；‎ ‎②.若，则，则，则在上单调递减；‎ ‎③.若，则，，又在上单调递增，‎ 结合零点存在性定理知：存在唯一实数，使得，‎ 此时函数在区间内有极小值点，矛盾.‎ 综上，或. ………6分 ‎ ‎(2) 由（1）可知，‎ ‎①.若，则在上单调递增，则，而，‎ 则是关于的减函数，故；‎ ‎②.若，则在上单调递减，则，而；‎ 则是关于的增函数，故；‎ 因为，故，‎ 综上，. ………12分 ‎（二）选考题：第22、23题中任选一题做答。如果多做，则按所做的第一题记分。‎ 19. 解：（1）直线的普通方程为：，曲线的直角坐标方程为：.………5分 ‎（2）曲线的参数方程为，‎ 点的直角坐标为，中点，，‎ 则点到直线的距离，‎ 当时，的最小值为，‎ 所以中点到直线的距离的最小值为. ………10分 第 6 页 （共 6 页）‎ 19. 解：（1）要证不等式等价于，因为 ‎，‎ 所以，当且仅当时取等号. ………5分 ‎（2）因为，所以，‎ 又因为，，，所以，‎ 所以，当且仅当时取等号. ………10分 第 6 页 （共 6 页）‎