数学理卷·2018届山东省、湖北省部分重点中学高三第二次（12月）联考（2017

数学理卷·2018届山东省、湖北省部分重点中学高三第二次（12月）联考（2017

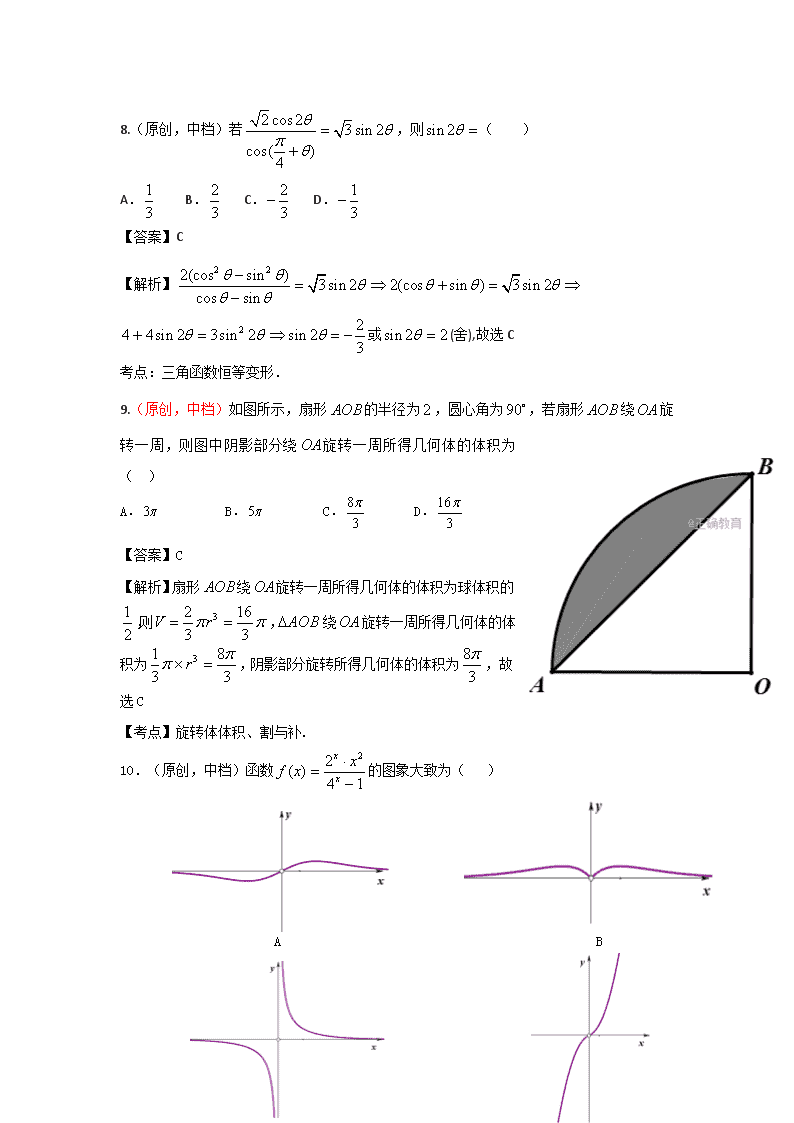
山东、湖北部分重点中学 2018 年第二次联考(理) 数学试题（理工农医类） 一、选择题：本大题共 12 小题，每小题 5分，在每小题给出的四个选项中，只有一项是符 合题目要求的. 1．（原创，容易）已知复数 z满足 (1 ) 3i z i    ，则 z在复平面内对应的点位于( ) A．第一象限 B．第二象限 C．第三象限 D．第四象限 【答案】B 【解析】 (1 ) 3i z i    3 2 1 iz i i         ,则 2z i   .故选 B 【考点】复数运算及几何意义. 2．（原创，容易）已知全集    2| 5 6 0 , 1 2U x Z x x A x Z x          ，  2,3,5B  ， 则  U A B ð （ ） A． 2,3,5 B． 3,5 C． 2,3, 4,5 D． 3, 4,5 【答案】B 【解析】    0,1, 2,3, 4,5 , 0,1, 2U A  ,则  U A B ð  3,5 . 【考点】二次不等式及集合运算. 3.（原创，容易）在等差数列 na 中， 7 =14S ，则 2 4 6a a a  （ ） A． 2 B． 4 C． 6 D．8 【答案】C 【解析】 7 4 4=14 7 14 2S a a    ,则 2 4 6 43 6a a a a    . 【考点】等差数列性质. 4.（原创，容易）如图，网格纸上的小正方形边长为 1，粗实线画出的是某几何体的三视图， 则该几何体的表面积为（ ） A．8+4 3 B．8+2 3 C． 4+4 3 D． 4+2 3 【答案】A 【解析】三视图还原为三棱锥 A BCD ，如左下图所示， 则三棱锥 A BCD 的表面积为 A BCDS   21 34 2 2 (2 2) 2 8 4 3 2 4         【考点】三视图还原及三棱锥的表面积. 5.（原创，中档）已知 1.1 0.6 1 2 2 , 3 , log 3a b c   ,则 , ,a b c的大小 为（ ） A．b c a  B.a c b  C. b a c  D. a b c  【答案】D 【解析】 1.1 0.6 1 2 2 0, 3 0, log 3 0a b c      , 51.1 0.6 3 52 2, 3 3 2 32a b      【考点】指数函数对数函数的性质. 6.（原创，中档）若函数 ( ) sin(2 ) 3 f x x    图象的横坐标伸长到原来的 2 倍, 纵坐标不变, 再向左平移 6  得到函数 ( )g x 的图象，则有（ ） A． ( ) cosg x x B． ( ) sing x x C． ( ) cos( ) 3 g x x    D． ( ) sin( ) 3 g x x    【答案】A 【解析】： 2 6sin(2 ) sin( ) sin( ) cos 3 3 2 y x y x y x x             左移 横坐标变为 倍 . 【考点】正余弦型函数的图象变换. 7.（原创，中档）已知命题 :p 若 a c b c       ，则 a b   ，命题 :q 若 2,a b a b       ， 则 2 1b   ，则有（ ） A． p为真 B. q 为真 C. p q 为真 D. p q 为真 【答案】D 【解析】p为假， 2,a b a b       2 2 1 1b b b b           ，q为真. 则 p q 为真，故选 D 【考点】向量数量积与模、不等式及简易逻辑. 8.（原创，中档）若 2 cos 2 3 sin 2 cos( ) 4       ，则 sin 2 （ ） A． 1 3 B． 2 3 C． 2 3  D． 1 3  【答案】C 【解析】 2 22(cos sin ) 3 sin 2 2(cos sin ) 3 sin 2 cos sin                2 24 4sin 2 3sin 2 sin 2 3        或 sin 2 2  (舍),故选 C 考点：三角函数恒等变形． 9.（原创，中档）如图所示，扇形 AOB的半径为 2，圆心角为90，若扇形 AOB绕OA旋 转一周，则图中阴影部分绕OA旋转一周所得几何体的体积为 （ ） A．3 B．5 C． 8 3  D． 16 3  【答案】C 【解析】扇形 AOB绕OA旋转一周所得几何体的体积为球体积的 1 2 ，则 32 16 3 3 V r   ， AOB 绕OA旋转一周所得几何体的 体积为 31 8 3 3 r    ，阴影部分旋转所得几何体的体积为 8 3  ， 故选 C 【考点】旋转体体积、割与补. 10．（原创，中档）函数 22( ) 4 1 x x xf x    的图象大致为（ ） A B C D 【答案】A 【解析】 2 22( ) ( ) ( ) ( ) 4 1 2 2 x x x x x xf x f x f x f x           为奇函数，排除 B； ( ) 0x f x   ；排除 D； 2 1 2 1(1 = ( ) ( ) (1) 3 2 4 2 f f f f  ） ， ，排除 C；故选 A 【考点】函数性质及图象. 11.（原创，中档）已知从 1开始的连续奇数蛇形排列形成宝塔形数表，第一行为 1，第二 行为 3，5，第三行为 7，9，11，第四行为 13，15，17，19，如图 所示，在宝塔形数表中位于第 i行，第 j列的数记为 ,i ja ，比如 3 2 4 2 5 49, 15, 23， ， ，  a a a ，若 , 2017i ja  ，则 i j （ ） A． 64 B． 65 C． 71 D． 72 【答案】D 【解析】奇数数列 2 1 2017 1009na n n     ， 按照蛇形排列，第 1 行到第 i行末共有 (1 )1 2 2 i ii      个奇数,则第 1 行到第 44行末 共有990个奇数；第 1 行到第45行末共有1035个奇数；则 2017 位于第 45 行；而第 45行 是从右到左依次递增，且共有45个奇数；故 2017位于第 45 行，从右到左第 19 列，则 45, 27 72i j i j     ，故选 D 【考点】等差数列与归纳推理. 12.（原创，难）已知函数 ( ) 2 cos 2 cos( ) 4 f x x x    ，给出下列命题：①函数 ( )f x 的 最小正周期为 2 ；②函数 ( )f x 关于 4 x   对称；③函数 ( )f x 关于 3( ,0) 4  对称；④函数 ( )f x 的值域为 4 6 4 6[ , ] 9 9  ，则其中正确的命题个数为（ ） A. 1 B. 2 C. 3 D. 4 【答案】D 【解析】 ( ) 2 cos 2 cos( ) 4 f x x x    的周期显然为 2 ； ( ) 2 cos(2 )cos( ) 2 sin 2 sin 4 2 2 f x x x x x        ； ( ) 2 cos( 2 )cos( ) 2 sin 2 sin 4 2 2 f x x x x x          ； ( ) ( ) 4 4 f x f x     ，故 ②正确. 3 3( ) 2 cos(2 )cos( ) 2 sin 2 cos 4 2 f x x x x x        3 3( ) 2 cos( 2 )cos( ) 2 sin 2 cos 4 2 f x x x x x         ； 3 3( ) ( ) 4 4 f x f x      ，故③正确. 2( ) (cos sin )(cos sin )f x x x x x   ， 设 2 2cos sin (cos sin ) 2x x t x x t      ，则 [ 2, 2]t  ， 32y t t  2 min max 6 4 6 4 62 3 0 , 3 9 9 y t t y y           ，故④正确 【考点】三角恒等变形、函数周期性、对称性及值域. 二、填空题：本大题共 4 小题，每小题 5 分. 13.（原创，容易）若 ( , 2), ( 1,1)a x b x     ，若 ( ) ( )a b a b       ，则 x  ． 【答案】 1 【解析】 2 2 ( ) ( ) 1a b a b a b x              【考点】向量坐标运算及向量垂直. 14.（原创，容易）已知实数 ,x y满足 1 0 2 4 0 0 x y x y x          ，则 2z x y  的最小值为 ． 【答案】5 【解析】由题意可得可行域为如图所示（含边界）， 1 12 2 2 z x y y x z      ，则在点 (1,2)A 处取得最小值5 【考点】基本型的线性规划 15.（原创，中档）已知在数列 na 的前 n项之和为 nS ，若 1 1 12, 2 1n n na a a      ，则 10S  ． 【答案】1078 【解析】 1 1 1 1 12, 2 1 2 1n n n n n na a a a a           1 1 2 3 2 2 1 1( ) ( ) ( ) ( )n n n n na a a a a a a a a a              2 3 12 2 2 1 1n n na n a         . 1 11 2 1 2 2 1 2 n nn n          . 2 9 10 10 111 2 2 2 1078 2 S         . 【考点】等差等比数列及均值不等式 16.（原创，难）四棱锥 S ABCD 中，底面 ABCD是边长为 2的正方形，侧面 SAD是以 SD 为斜边的等腰直角三角形，若2 2 4SC  ，则四棱锥 S ABCD 的体积取值范围 为 ． 【答案】 4 3 8[ , ] 3 3 【解析】如图所示，四棱锥 S ABCD 中，可得： ;AD SA AD AB AD   平面 SAB平面 SAB 平面 ABCD，过 S作 SO AB 于O，则 SO 平面 ABCD，故 1 4 3 3S ABCD ABCDV S SO SO    ， 在 SAB 中， 2SA AB  ，设 SAB   ，则有， 2 3 2cosSC   ,又 2 2 4SC  1 1 2cos [ , ] 2 2 3 3         ，则 2sin [ 3, 2]SO   ，四棱锥 S ABCD 的体积取值范围为 4 3 8[ , ] 3 3 【考点】线面垂直、面面垂直、解三角不等式及体积范围. 三、解答题：本大题共 6 小题，共 70 分，解答应写出文字说明，证明过程或演算步骤. 17.（本题满分 12 分） （原创，容易）已知单调的等比数列 na 的前n项的和为 nS ，若 3 39S  ，且 43a 是 6 5,a a 的等差中项. (Ⅰ)求数列 na 的通项公式； (Ⅱ)若数列 nb 满足 3 2 1logn nb a  ，且 nb 前n项的和为 nT ，求 1 2 3 1 1 1 1 nT T T T     . 【答案】(Ⅰ) 3nna  ；(Ⅱ) 4 3 （18）解：(Ⅰ) 2 4 6 56 6 0 3a a a q q q        或 2q   （舍）；………………3 分 3 1 3 1 (1 ) 39 3 1 a qS a q       …………………5 分 3nna  ……………………6 分 (Ⅱ) 2 1 3log 3 2 1n nb n   ；………………7 分 3 5 2 1 ( 2)nT n n n       ………………8 分 1 1 1 1 1( ) ( 2) 2 2nT n n n n      ………………10 分 1 2 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1( ) ( ) ( ) ( ) 2 1 3 2 2 4 2 3 5 2 2nT T T T n n                 1 2 3 1 1 1 1 1 3 1 1( ) 2 2 1 2nT T T T n n            ……………………12 分 【考点】等比数列基本量运算、数列求和 18．（本题满分 12 分） （原创，中档）设函数 3( ) 2sin( ) cos 3 2 f x x x    (Ⅰ) 求 ( )f x 的单调增区间； (Ⅱ) 已知 ABC 的内角分别为 , ,A B C，若 3( ) 2 2 Af  ，且 ABC 能够盖住的最大圆面 积为 ，求 AB AC   的最小值. 【答案】(Ⅰ) 5[ , ], 12 12 k k k Z      ；(Ⅱ)6 （18）解：(Ⅰ) 3 1 3( ) 2sin( ) cos sin 2 cos 2 3 2 2 2 f x x x x x      ……3 分 sin(2 ) 3 x    ……………4 分 52 2 2 , 2 3 2 12 12 k x k k x k k Z                    …………5 分 ( )f x 的单调增区间为 5[ , ], 12 12 k k k Z      ……6 分 (Ⅱ) 由余弦定理可知： 2 2 2a b c bc   ……7 分 由题意可知： ABC 的内切圆半径为1……8 分 ABC 的内角 , ,A B C的对边分别为 , ,a b c，则 2 3b c a   ……9 分 2 2 2( 2 3)b c b c bc     ……………10 分 4 3 3 4( ) 8 12bc b c bc bc       或 4 3 bc  （舍）……11 分 1 [6, ) 2 AB AC bc      ， 当且仅当b c 时， AB AC   的最小值为6 .……………12 分 令也可以这样转化： 31 2 r a b c bc     ……9 分 代入 2 2 23( ) 2 b c bc b c bc     ；……………10 分 4 3 3 4( ) 8 12bc b c bc bc       或 4 3 bc  （舍）；……………11 分 1 [6, ) 2 AB AC bc      ， 当且仅当b c 时， AB AC   的最小值为6 .……………12 分 【考点】三角函数式化简、正余弦型函数性质、解三角形及均值不等式求最值. 19．（本题满分 12 分） （原创，中档）如图，三棱台 1 1 1ABC A B C 中， 侧面 1 1A B BA与侧面 1 1AC CA是全等的梯 形，若 1 1 1 1,A A AB A A AC  ,且 1 1 12 4AB A B A A  . （Ⅰ）若 12CD DA   ， 2AE EB   ，证明：DE∥平面 1 1BCC B ； （Ⅱ）若二面角 1 1C AA B  为 3  ，求平面 1 1A B BA与平面 1 1C B BC 所成的锐二面角的余弦 值. 19.（Ⅰ）证明：连接 1 1,AC BC ，梯形 1 1AC CA， 1 12AC AC , 易知： 1 1 1, 2AC AC D AD DC     ……2分； 又 2AE EB   ，则DE∥ 1BC ……4分； 1BC 平面 1 1BCC B ，DE 平面 1 1BCC B ， 可得：DE∥平面 1 1BCC B ……6分； （Ⅱ）侧面 1 1AC CA是梯形， 1 1 1A A AC ， 1AA AC  , 1A A AB , 则 BAC 为二面角 1 1C AA B  的平面角， BAC  3  ……7 分； 1 1 1,ABC A B C   均为正三角形，在平面 ABC内，过点 A作 AC的垂线，如图建立空间 直角坐标系，不妨设 1 1AA  ，则 1 1 1 1 2,AB AC  4AC AC  ,故点 1 (0,0,1)A ， (0,4,0),C 1(2 3,2,0), ( 3,1,1)B B ……9 分； 设平面 1 1A B BA的法向量为 1 1 1( , , )m x y z  ，则有： 1 1 1 1 1 1 0 3 0 (1, 3,0) 0 3 0 m AB x y m m AB x y z                       ……10 分； 设平面 1 1C B BC 的法向量为 2 2 2( , , )n x y z  ，则有： 2 2 1 2 2 2 0 3 0 (1, 3,2 3) 0 3 3 0 m CB x y n m CB x y z                      ……11 分； 1cos , 4 m nm n m n          ， 故平面 1 1A B BA与平面 1 1C B BC 所成的锐二面角的余弦值为 1 4 ……12 分； 【考点】线面平行证明及二面角计算. 20. （本题满分 12 分） 设函数 2( ) 2( 2) 2 3xf x x e ax ax b      （原创，中档）（Ⅰ）若 ( )f x 在 0x  处的法线（经过切点且垂直于切线的直线）的方程为 2 4 0x y   ，求实数 ,a b的值； （原创，难）（Ⅱ）若 1x  是 ( )f x 的极小值点，求实数 a的取值范围. （Ⅰ）解： ( ) 2( 1) 2 2xf x x e ax a     ；……………………2 分； 由题意可知： (0) 2f   ；……………………3 分； (0) 2 2 2 2f a a       ；………………4 分； 易得切点坐标为 (0, 2) ，则有 (0) 2 1f b    ；………………5 分； （Ⅱ）由（Ⅰ）可得： ( ) 2( 1) 2 2 2( 1)( )x xf x x e ax a x e a        ；………………6 分； （1）当 0a  时， 0 ( ) 0 1xe a f x x      ， ( ,1) ( ) 0x f x    ； (1, ) ( ) 0x f x    ； 1x  是 ( )f x 的极小值点，∴ 0a  适合题意；………………7 分； （2）当0 a e  时， 1( ) 0 1f x x    或 2 lnx a ，且 ln 1a  ； ( , ln ) ( ) 0x a f x    ； (ln ,1) ( ) 0x a f x   ； (1, ) ( ) 0x f x    ； 1x  是 ( )f x 的极小值点，∴0 a e  适合题意；………………9 分； （2）当 a e 时， 1( ) 0 1f x x    或 2 lnx a ，且 ln 1a  ； ( ,1) ( ) 0x f x    ； (1, ln ) ( ) 0x a f x   ； (ln , ) ( ) 0x a f x    ； 1x  是 ( )f x 的极大值点，∴ a e 不适合题意；…………11 分 综上，实数a的取值范围为 a e ；………………12 分； 【考点】函数切线及函数极值. 21. （本题满分 12 分） 已知函数 ( ) (ln 1) 1f x x x ax ax      ． （原创，中档）（Ⅰ）若 ( )f x 在[1, ) 上是减函数，求实数 a的取值范围. （原创，难）（Ⅱ）若 ( )f x 的最大值为 2，求实数 a的值. （Ⅰ） ( ) ln 2 2 0f x x ax a      在[1, ) 恒成立……1分； 2 ln 1 2 xa x     在[1, ) 恒成立……2分； 设 2 ln( ) , [1, ) 1 2 xg x x x      ，则 2 1 2 2ln ( ) (1 2 ) x xg x x      ，由 1x  得： ( ) 0g x  ……3 分； ( )g x 在[1, ) 上为增函数 1x  ， ( )g x 有最小值 (1) 2g   . ∴ 2a   ；……4 分； （Ⅱ）注意到 (1) 2f  ，又 ( )f x 的最大值为 2，则 (1) 0f   2 0 2a a      ；………………6 分 下面证明： 2a   时， ( ) 2f x  ，即 ( ) (ln 2 1) 2 1 0f x x x x x       , 1ln 2 3 0x x x      ；……………7 分 设 1( ) ln 2 3, (0, )h x x x x x       ；……………8 分 2 2 2 2 1 1 2 1 (2 1)(1 )( ) 2 x x x xh x x x x x           ……………9分 (0,1) ( ) 0 ( )x h x h x    在 (0,1]上为增函数； (1, ) ( ) 0 ( )x h x h x     在[1, ) 上为减函数；……………10 分 1 ( )x h x  有最大值 (1) 0h  ；……………11 分 ( ) (1) 0h x h  ( ) (ln 2 1) 2 1 0f x x x x x        ∴ 2a   适合题意；……………12 分 【考点】导函数单调性、函数最值及不等式证明. 选做题（请考生在第 22、23 题中任选一题作答，如果多选，则按所做的第一题计分） 22．（本小题满分 10 分）【选修 4−4：坐标系与参数方程】 （原创，容易）已知直线 l的参数方程为  x t t y a t     为参数 ．以原点为极点， x轴的正 半轴为极轴，建立极坐标系, 圆C的极坐标方程为 4cos  . （Ⅰ）求直线 l与圆C的普通方程； （Ⅱ）若直线 l分圆C所得的弧长之比为3 :1，求实数 a的值． 解：（Ⅰ）由题意知： 2 2 24cos 4 cos 4 0x x y           …………3 分， 0 x t x y a x y a y a t           ；…………5分 （Ⅱ） 2 2 2 24 0 ( 2) 4x x y x y       ；…………6分， 直线 l分圆C所得的弧长之比为3 :1弦长为2 2；…………8分， 2 2 2d r    ；…………9 分， 2 2 0 2 a d a       或 4a  ；…………10 分， 【考点】方程互化、圆弦长. 23．（本小题满分 10 分）【选修 4—5：不等式选讲】 （原创，容易）已知函数 ( ) 2 4 1f x x x    , （Ⅰ）解不等式 ( ) 9f x  ； （Ⅱ）若不等式 ( ) 2f x x a  的解集为 A，  2 3 0B x x x   ，且满足 B A ，求实 数a的取值范围. 23. 解：（Ⅰ） ( ) 9f x  可化为 2 4 1 9x x    2 3 3 9 x x     ，或 1 2 5 9 x x       ，或 1 3 3 9 x x      ；…………………………2 分 2 4x  ，或 1 2x   ，或 2 1x    ； ……………………4 分 不等式的解集为[ 2,4] ；……………………………5 分 （Ⅱ）易知 (0,3)B  ；…………………………6分 所以 B A ，又 2 4 1 2x x x a     在 (0,3)x 恒成立；…………………………7分 2 4 1x x a     在 (0,3)x 恒成立；…………………………8 分 1 2 4 1x a x x a         在 (0,3)x 恒成立；…………………………9分 (0,3) (0,3 3 )3 5 a x a x x x        在 恒成立 在 恒成立 0 5 a a a       ………………………10 分 【考点】绝对值不等式解法、不等式恒成立. 齐鲁名校教科研协作体 山东、湖北部分重点中学 2018 届高三第二次调研联考 数学（理）参考答案及评分标准 1．【答案】B 2．【答案】B 3.【答案】C 4.【答案】A 5.【答案】D 6.【答案】A 7.【答案】D 8.【答案】C 9.【答案】C 10．【答案】A 11.【答案】D 12.【答案】D 13.【答案】 1 14.【答案】5 15.【答案】1078 16.【答案】 4 3 8[ , ] 3 3 17.【答案】(Ⅰ) 3nna  ；(Ⅱ) 4 3 解：(Ⅰ) 2 4 6 56 6 0 3a a a q q q        或 2q   （舍）；………………3 分 3 1 3 1 (1 ) 39 3 1 a qS a q       …………………5 分 3nna  ……………………6 分 (Ⅱ) 2 1 3log 3 2 1n nb n   ；………………7 分 3 5 2 1 ( 2)nT n n n       ………………8 分 1 1 1 1 1( ) ( 2) 2 2nT n n n n      ………………10 分 1 2 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1( ) ( ) ( ) ( ) 2 1 3 2 2 4 2 3 5 2 2nT T T T n n                 1 2 3 1 1 1 1 1 3 1 1( ) 2 2 1 2nT T T T n n            ……………………12 分 【考点】等比数列基本量运算、数列求和 18．【答案】(Ⅰ) 5[ , ], 12 12 k k k Z      ；(Ⅱ)6 解：(Ⅰ) 3 1 3( ) 2sin( ) cos sin 2 cos 2 3 2 2 2 f x x x x x      ……3 分 sin(2 ) 3 x    ……………4 分 52 2 2 , 2 3 2 12 12 k x k k x k k Z                    …………5 分 ( )f x 的单调增区间为 5[ , ], 12 12 k k k Z      ……6 分 (Ⅱ) 由余弦定理可知： 2 2 2a b c bc   ……7 分 由题意可知： ABC 的内切圆半径为1……8 分 ABC 的内角 , ,A B C的对边分别为 , ,a b c，则 2 3b c a   ……9 分 2 2 2( 2 3)b c b c bc     ……………10 分 4 3 3 4( ) 8 12bc b c bc bc       或 4 3 bc  （舍）……11 分 1 [6, ) 2 AB AC bc      ， 当且仅当b c 时， AB AC   的最小值为6 .……………12 分 令也可以这样转化： 31 2 r a b c bc     ……9 分 代入 2 2 23( ) 2 b c bc b c bc     ；……………10 分 4 3 3 4( ) 8 12bc b c bc bc       或 4 3 bc  （舍）；……………11 分 1 [6, ) 2 AB AC bc      ， 当且仅当b c 时， AB AC   的最小值为6 .……………12 分 19． 19.（Ⅰ）证明：连接 1 1,AC BC ，梯形 1 1AC CA， 1 12AC AC , 易知： 1 1 1, 2AC AC D AD DC     ……2分； 又 2AE EB   ，则DE∥ 1BC ……4分； 1BC 平面 1 1BCC B ，DE 平面 1 1BCC B ， 可得：DE∥平面 1 1BCC B ……6分； （Ⅱ）侧面 1 1AC CA是梯形， 1 1 1A A AC ， 1AA AC  , 1A A AB , 则 BAC 为二面角 1 1C AA B  的平面角， BAC  3  ……7 分； 1 1 1,ABC A B C   均为正三角形，在平面 ABC内，过点 A作 AC的垂线，如图建立空间 直角坐标系，不妨设 1 1AA  ，则 1 1 1 1 2,AB AC  4AC AC  ,故点 1 (0,0,1)A ， (0,4,0),C 1(2 3,2,0), ( 3,1,1)B B ……9 分； 设平面 1 1A B BA的法向量为 1 1 1( , , )m x y z  ，则有： 1 1 1 1 1 1 0 3 0 (1, 3,0) 0 3 0 m AB x y m m AB x y z                       ……10 分； 设平面 1 1C B BC 的法向量为 2 2 2( , , )n x y z  ，则有： 2 2 1 2 2 2 0 3 0 (1, 3,2 3) 0 3 3 0 m CB x y n m CB x y z                      ……11 分； 1cos , 4 m nm n m n          ， 故平面 1 1A B BA与平面 1 1C B BC 所成的锐二面角的余弦值为 1 4 ……12 分； 20. （Ⅰ）解： ( ) 2( 1) 2 2xf x x e ax a     ；……………………2 分； 由题意可知： (0) 2f   ；……………………3 分； (0) 2 2 2 2f a a       ；………………4 分； 易得切点坐标为 (0, 2) ，则有 (0) 2 1f b    ；………………5 分； （Ⅱ）由（Ⅰ）可得： ( ) 2( 1) 2 2 2( 1)( )x xf x x e ax a x e a        ；………………6 分； （1）当 0a  时， 0 ( ) 0 1xe a f x x      ， ( ,1) ( ) 0x f x    ； (1, ) ( ) 0x f x    ； 1x  是 ( )f x 的极小值点，∴ 0a  适合题意；………………7 分； （2）当0 a e  时， 1( ) 0 1f x x    或 2 lnx a ，且 ln 1a  ； ( , ln ) ( ) 0x a f x    ； (ln ,1) ( ) 0x a f x   ； (1, ) ( ) 0x f x    ； 1x  是 ( )f x 的极小值点，∴0 a e  适合题意；………………9 分； （2）当 a e 时， 1( ) 0 1f x x    或 2 lnx a ，且 ln 1a  ； ( ,1) ( ) 0x f x    ； (1, ln ) ( ) 0x a f x   ； (ln , ) ( ) 0x a f x    ； 1x  是 ( )f x 的极大值点，∴ a e 不适合题意；…………11 分 综上，实数a的取值范围为 a e ；………………12 分； 21. （Ⅰ） ( ) ln 2 2 0f x x ax a      在[1, ) 恒成立……1 分； 2 ln 1 2 xa x     在[1, ) 恒成立……2分； 设 2 ln( ) , [1, ) 1 2 xg x x x      ，则 2 1 2 2ln ( ) (1 2 ) x xg x x      ，由 1x  得： ( ) 0g x  ……3 分； ( )g x 在[1, ) 上为增函数 1x  ， ( )g x 有最小值 (1) 2g   . ∴ 2a   ；……4 分； （Ⅱ）注意到 (1) 2f  ，又 ( )f x 的最大值为 2，则 (1) 0f   2 0 2a a      ；………………6 分 下面证明： 2a   时， ( ) 2f x  ，即 ( ) (ln 2 1) 2 1 0f x x x x x       , 1ln 2 3 0x x x      ；……………7 分 设 1( ) ln 2 3, (0, )h x x x x x       ；……………8 分 2 2 2 2 1 1 2 1 (2 1)(1 )( ) 2 x x x xh x x x x x           ……………9分 (0,1) ( ) 0 ( )x h x h x    在 (0,1]上为增函数； (1, ) ( ) 0 ( )x h x h x     在[1, ) 上为减函数；……………10 分 1 ( )x h x  有最大值 (1) 0h  ；……………11 分 ( ) (1) 0h x h  ( ) (ln 2 1) 2 1 0f x x x x x        ∴ 2a   适合题意；……………12 分 22． 解：（Ⅰ）由题意知： 2 2 24cos 4 cos 4 0x x y           …………3 分， 0 x t x y a x y a y a t           ；…………5分 （Ⅱ） 2 2 2 24 0 ( 2) 4x x y x y       ；…………6分， 直线 l分圆C所得的弧长之比为3 :1弦长为2 2；…………8分， 2 2 2d r    ；…………9 分， 2 2 0 2 a d a       或 4a  ；…………10 分， 23. 解：（Ⅰ） ( ) 9f x  可化为 2 4 1 9x x    2 3 3 9 x x     ，或 1 2 5 9 x x       ，或 1 3 3 9 x x      ；…………………………2 分 2 4x  ，或 1 2x   ，或 2 1x    ； ……………………4 分 不等式的解集为[ 2,4] ；……………………………5 分 （Ⅱ）易知 (0,3)B  ；…………………………6分 所以 B A ，又 2 4 1 2x x x a     在 (0,3)x 恒成立；…………………………7分 2 4 1x x a     在 (0,3)x 恒成立；…………………………8 分 1 2 4 1x a x x a         在 (0,3)x 恒成立；…………………………9分 (0,3) (0,3 3 )3 5 a x a x x x        在 恒成立 在 恒成立 0 5 a a a       ………………………10 分