高考理科数学专题复习练习 14.1几何证明选讲

高考理科数学专题复习练习 14.1几何证明选讲

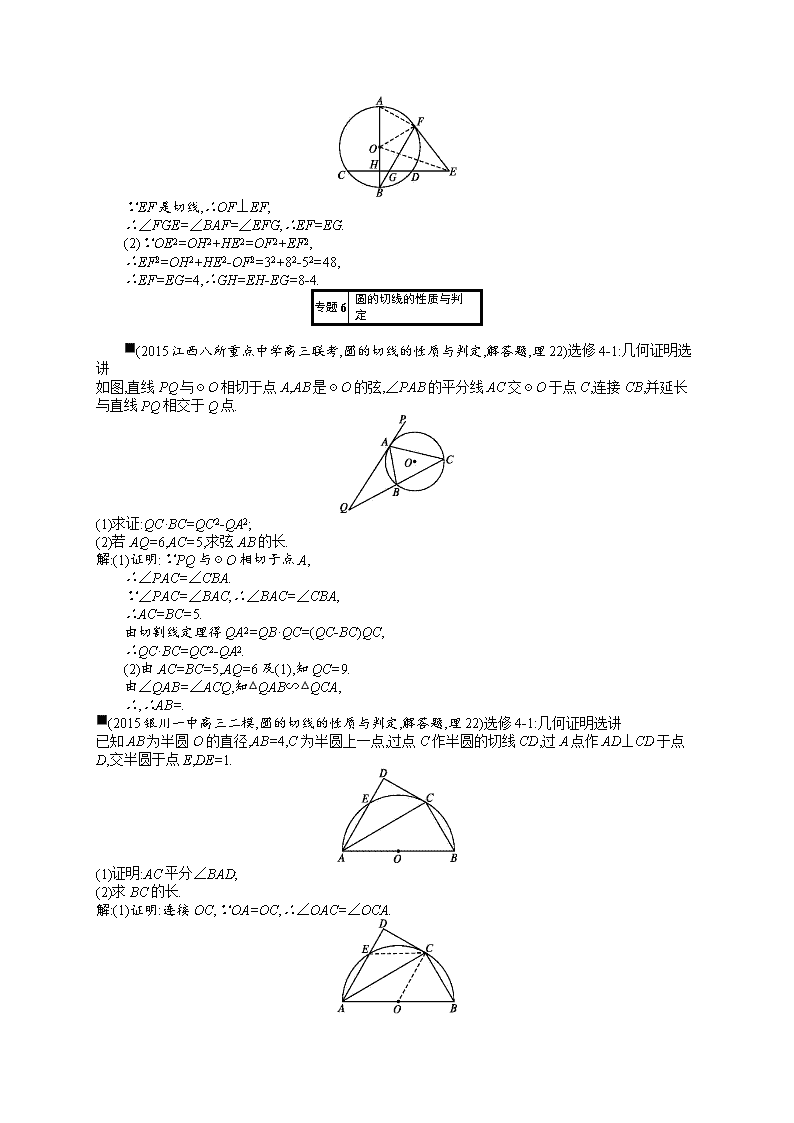
第十四章选修模块 ‎14.1几何证明选讲 专题2‎ 相似三角形的判定与性质 ‎■(2015江西重点中学盟校高三第一次联考,相似三角形的判定与性质,解答题,理22)选修4—1:几何证明选讲 如图,☉O的半径为6,线段AB与☉O相交于点C,D,AC=4,∠BOD=∠A,OB与☉O相交于点E.‎ ‎(1)求BD的长;‎ ‎(2)当CE⊥OD时,求证:AO=AD.‎ 解:(1)∵OC=OD,∴∠OCD=∠ODC,‎ ‎∴∠OCA=∠ODB.‎ ‎∵∠BOD=∠A,∴△OBD∽△AOC,∴.‎ ‎∵OC=OD=6,AC=4,∴,∴BD=9.‎ ‎(2)证明:∵OC=OE,CE⊥OD,‎ ‎∴∠COD=∠BOD=∠A.‎ ‎∴∠AOD=180°-∠A-∠ODC=180°-∠COD-∠OCD=∠ADO.‎ ‎∴AD=AO.‎ ‎■(2015辽宁东北育才高三第五次模拟,相似三角形的判定与性质,解答题,理22)选修4—1:几何证明选讲 如图,AB是☉O的一条切线,切点为B,直线ADE,CFD,CGE都是☉O的割线,已知AB=AC.‎ ‎(1)求证:FG∥AC;‎ ‎(2)若CG=1,CD=4,求的值.‎ 解:(1)证明:因为AB为切线,AE为割线,所以AB2=AD·AE,又因为AC=AB,所以AD·AE=AC2.‎ 所以,又因为∠EAC=∠DAC,‎ 所以△ADC∽△ACE,所以∠ADC=∠ACE,‎ 又因为∠ADC=∠EGF,‎ 所以∠EGF=∠ACE,所以FG∥AC.‎ ‎(2)由题意可得G,E,D,F四点共圆.‎ 所以∠CGF=∠CDE,∠CFG=∠CED.‎ 所以△CGF∽△CDE,所以.‎ 又因为CG=1,CD=4,所以=4.‎ 专题4‎ 圆周角、弦切角及圆的切线 ‎■(2015银川二中高三一模,圆周角、弦切角及圆的切线,解答题,理22)选修4—1:几何证明选讲 如图,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于点E,BD交AC于点G,交CE于点F,CF=FG,求证:‎ ‎(1)C是劣弧BD的中点;‎ ‎(2)BF=FG.‎ 证明:(1)∵CF=FG,∴∠CGF=∠FCG.‎ ‎∵AB为圆O的直径,∴∠ACB=∠ADB=.‎ ‎∵CE⊥AB,∴∠CEA=.‎ ‎∵∠CBA=-∠CAB,∠ACE=-∠CAB,‎ ‎∴∠CBA=∠ACE.‎ ‎∵∠CGF=∠DGA,∠DGA=∠ABC,‎ ‎∴-∠DGA=-∠ABC,‎ ‎∴∠CAB=∠DAC,∴C为劣弧BD的中点.‎ ‎(2)∵∠GBC=-∠CGB,∠FCB=-∠GCF,‎ ‎∴∠GBC=∠FCB,∴CF=FB,∴BF=FG.‎ 专题5‎ 圆内接四边形的判定及性质 ‎■(2015辽宁大连高三双基测试,圆内接四边形的判定及性质,解答题,理22)选修4—1:几何证明选讲 如图,已知☉O1与☉O2相交于A,B两点,P是☉O1上一点,PB的延长线交☉O2于点C,PA交☉O1于点D,CD的延长线交☉O1于点N.‎ ‎(1)点E是上异于A,N的任意一点,PE交CN于点M,求证:A,D,M,E四点共圆;‎ ‎(2)求证:PN2=PB·PC.‎ 证明:(1)连接AB,∵A,B,P,E四点共圆,‎ ‎∴∠ABC=∠E.‎ 又∵∠ABC=∠ADC,∴∠ADC=∠E,‎ ‎∴A,D,M,E四点共圆.‎ ‎(2)连接BN,∵∠PNB=∠PAB=∠C,∠BPN=∠NPC,‎ ‎∴△PNB∽△PCN,,‎ ‎∴PN2=PB·PC.‎ ‎■(2015辽宁重点中学协作体高考模拟,圆内接四边形的判定及性质,解答题,理22)选修4-1:几何证明选讲 如图,已知AB是☉O的直径,CE⊥AB于点H,与☉O交于点C,D,且AB=10,CD=8,DE=4,EF与☉O切于点F,BF与HD交于点G.‎ ‎(1)证明:EF=EG;‎ ‎(2)求GH的长.‎ 解:(1)证明:连接AF,OE,OF,则A,F,G,H四点共圆.‎ ‎∵EF是切线,∴OF⊥EF,‎ ‎∴∠FGE=∠BAF=∠EFG,∴EF=EG.‎ ‎(2)∵OE2=OH2+HE2=OF2+EF2,‎ ‎∴EF2=OH2+HE2-OF2=32+82-52=48,‎ ‎∴EF=EG=4,∴GH=EH-EG=8-4.‎ 专题6‎ 圆的切线的性质与判定 ‎■(2015江西八所重点中学高三联考,圆的切线的性质与判定,解答题,理22)选修4-1:几何证明选讲 如图,直线PQ与☉O相切于点A,AB是☉O的弦,∠PAB的平分线AC交☉O于点C,连接CB,并延长与直线PQ相交于Q点.‎ ‎(1)求证:QC·BC=QC2-QA2;‎ ‎(2)若AQ=6,AC=5,求弦AB的长.‎ 解:(1)证明:∵PQ与☉O相切于点A,‎ ‎∴∠PAC=∠CBA.‎ ‎∵∠PAC=∠BAC,∴∠BAC=∠CBA,‎ ‎∴AC=BC=5.‎ 由切割线定理得QA2=QB·QC=(QC-BC)QC,‎ ‎∴QC·BC=QC2-QA2.‎ ‎(2)由AC=BC=5,AQ=6及(1),知QC=9.‎ 由∠QAB=∠ACQ,知△QAB∽△QCA,‎ ‎∴,∴AB=.‎ ‎■(2015银川一中高三二模,圆的切线的性质与判定,解答题,理22)选修4-1:几何证明选讲 已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过A点作AD⊥CD于点D,交半圆于点E,DE=1.‎ ‎(1)证明:AC平分∠BAD;‎ ‎(2)求BC的长.‎ 解:(1)证明:连接OC,∵OA=OC,∴∠OAC=∠OCA.‎ ‎∵CD为半圆的切线,∴OC⊥CD,∴OC∥AD.‎ ‎∴∠OCA=∠CAD,∴∠OAC=∠CAD,‎ ‎∴AC平分∠BAD.‎ ‎(2)连接CE,由∠OAC=∠CAD知BC=CE,‎ 又∵A,B,C,E四点共圆,‎ ‎∴cos∠B=cos∠CED,∴.‎ 又∵DE=1,AB=4,∴BC=2.‎ ‎■(2015东北三省三校高三第一次联考,圆的切线的性质与判定,解答题,理22)选修4-1:几何证明选讲 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.‎ 求证:(1)DE是圆O的切线;‎ ‎(2)DE·BC=DM·AC+DM·AB.‎ 证明:(1)连接OE.‎ ‎∵点D是BC的中点,点O是AB的中点,‎ ‎∴OD