2020学年高二数学下学期期末考试试题 理新人教目标版

2020学年高二数学下学期期末考试试题 理新人教目标版

‎2019-2学期高二年级期末考试试题 数学 说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分150分，考试时间120分钟.答案写在答题卡上，交卷时只交答题卡.‎ 附：K2＝ P(K2≥k0)‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.05‎ ‎0.010‎ k0‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎ ‎ 第Ⅰ卷（选择题）‎ 一、选择题（本大题共12 小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案涂在答题卡上.）‎ ‎1．5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同的报名方法共有(　　)‎ A．10种　 B．20种 C．25种 D．32种 ‎2．袋中有大小相同的红球6个，白球5个，从袋中每次任意取出1个球，取后不放回直到取出的球是白球为止，所需要的取球次数为随机变量X，则X的可能取值为(　　)‎ A．1，2，3，…，6 B．1，2，3，…，7 ‎ C．0，1，2，…，5 D．1，2，3，…，5‎ ‎3．若随机变量η的分布列如下表：‎ η ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎0.1‎ ‎0.2‎ ‎0.2‎ ‎0.3‎ ‎0.1‎ ‎0.1‎ 则当P(η7.879，在犯错误的概率不超过0.005的前提下，认为作文成绩优秀与课外阅读量大有关．‎ 答案：D ‎7．为预测某种产品的回收率y，需要研究它和原料有效成分含量x之间的相关关系，现取了8组观察值．计算知i＝52，i＝228，＝478，iyi＝1 849，则y对x的回归方程是(　　)‎ A．＝11.47＋2.62x B．＝－11.47＋2.62x ‎ ‎ C．＝2.62＋11.47x D．＝11.47－2.62x 解析：由＝，＝－，直接计算得≈2.62，≈11.47，所以＝2.62x＋11.47.‎ 答案：A ‎8．将两枚质地均匀的骰子各掷一次，设事件A＝{两个点数互不相同}，B＝{出现一个5点}，则P(B|A)＝(　　)‎ A． B． C． D． 解析：出现点数互不相同的共有6×5＝30种，出现一个5点共有5×2＝10种，‎ ‎∴P(B|A)＝＝.‎ 答案：A ‎9．甲、乙两人独立地解决同一问题，甲解决这个问题的概率是p1，乙解决这个问题的概率是p2，那么恰好有1人解决这个问题的概率是(　　)‎ A．p1p2 B．p1(1－p2)＋p2(1－p1) C．1－p1p2 D．1－(1－p1)(1－p2)‎ 解析：本题考查概率的应用．甲解决问题乙未解决问题的概率为p1(1－p2)，甲未解决问题乙解决问题的概率为p2(1－p1)，则恰有一人解决问题的概率为p1(1－p2)＋p2(1－p1)．故选B.‎ ‎10．如果的展开式中只有第4项的二项式系数最大，那么展开式中的所有项的系数和是(　　)‎ A．0 B．256 C．64 D． 解析：‎ 因为展开式中只有第4项的二项式系数最大，所以n＝6.令x＝1，则展开式中所有项的系数和是6＝6＝.‎ 答案：D ‎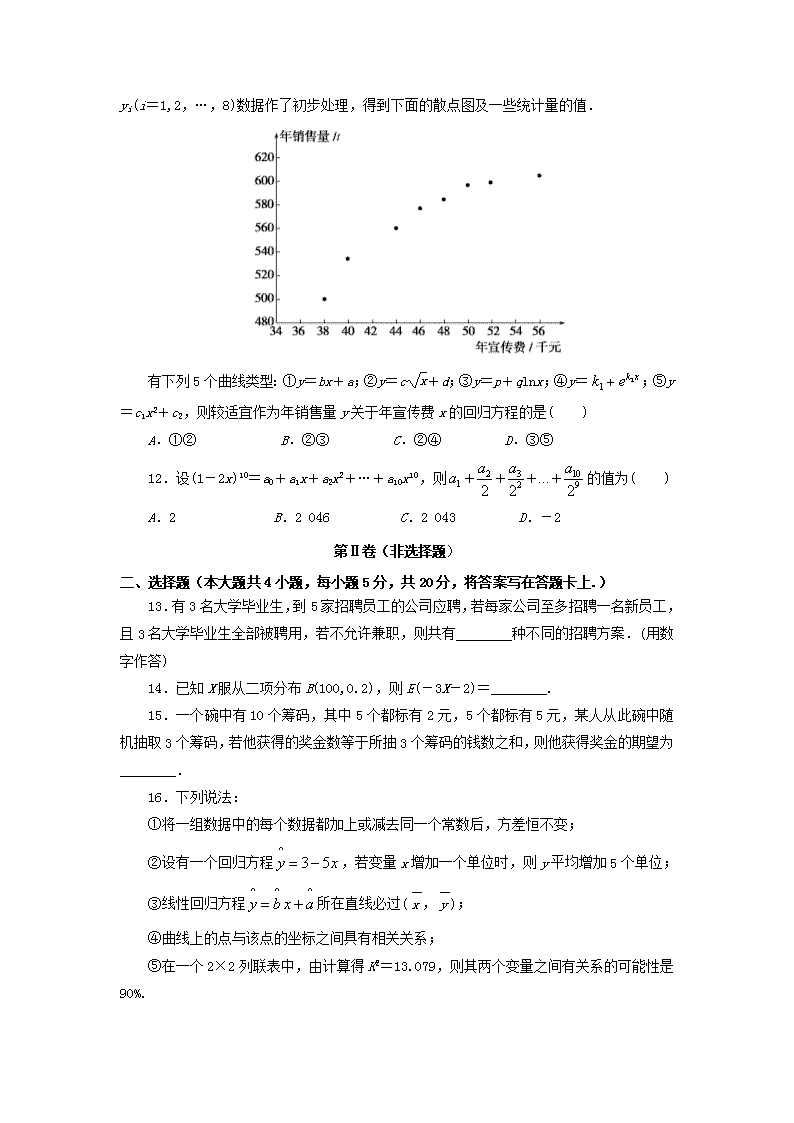11．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x(单位：千元)对年销售量y(单位：t)和年利润z(单位：千元)的影响．对近8年的年宣传费xi和年销售量yi(i＝1,2，…，8)数据作了初步处理，得到下面的散点图及一些统计量的值．‎ 有下列5个曲线类型：①y＝bx＋a；②y＝c＋d；③y＝p＋qlnx；④y＝；⑤y＝c1x2＋c2，则较适宜作为年销售量y关于年宣传费x的回归方程的是(　　)‎ A．①② B．②③ C．②④ D．③⑤‎ 解析：从散点图知，样本点分布在开口向右的抛物线(上支)附近或对数曲线(上部分)的附近，所以y＝c＋d或y＝p＋qlnx较适宜，故选B.‎ 答案：B ‎12．设(1－2x)10＝a0＋a1x＋a2x2＋…＋a10x10，则的值为(　　)‎ A．2 B．2 046 C．2 043 D．－2‎ 解析：令x＝0得a0＝1；‎ 令x＝得a0＋＋＋…＋＝0，‎ 所以a1＋＋＋…＋＝－2a0＝－2.‎ 答案：D 第Ⅱ卷（非选择题）‎ 二、选择题（本大题共4小题，每小题5分，共20分，将答案写在答题卡上.）‎ ‎13．有3名大学毕业生，到5家招聘员工的公司应聘，若每家公司至多招聘一名新员工，且3名大学毕业生全部被聘用，若不允许兼职，则共有________种不同的招聘方案．(用数字作答)‎ 解析：将5家招聘员工的公司看作5个不同的位置，从中任选3个位置给3名大学毕业生，则本题即为从5个不同元素中任取3个元素的排列问题．所以不同的招聘方案共有A＝5×4×3＝60(种)．‎ 答案：60‎ ‎14．已知X服从二项分布B(100,0.2)，则E(－3X－2)＝________.‎ 解析：由于X～B(100,0.2)，‎ 则E(X)＝np＝100×0.2＝20，‎ E(－3X－2)＝－3E(X)－2＝－62.‎ 答案：－62‎ ‎15．一个碗中有10个筹码，其中5个都标有2元，5个都标有5元，某人从此碗中随机抽取3个筹码，若他获得的奖金数等于所抽3个筹码的钱数之和，则他获得奖金的期望为________．‎ 解析：获得奖金数为随机变量ξ，则ξ＝6,9,12,15，所以ξ的分布列为：‎ ξ ‎6‎ ‎9‎ ‎12‎ ‎15‎ P E(ξ)＝6×＋9×＋12×＋15×＝＝.‎ 答案： ‎16．下列说法：‎ ‎①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；‎ ‎②设有一个回归方程，若变量x增加一个单位时，则y平均增加5个单位；‎ ‎③线性回归方程所在直线必过(，)；‎ ‎④曲线上的点与该点的坐标之间具有相关关系；‎ ‎⑤在一个2×2列联表中，由计算得K2＝13.079，则其两个变量之间有关系的可能性是90%.‎ 其中错误的是________．‎ 解析：由方差的性质知①正确；由线性回归方程的特点知③正确；②④⑤均错误．‎ 答案：②④⑤‎ 三、解答题（本大题共6小题，共70分）‎ ‎17．(10‎ 分)为了了解创建文明城市过程中学生对创建工作的满意情况，相关部门对某中学的100名学生进行调查．得到如下的统计表：‎ 满意 不满意 合计 男生 ‎50‎ a e 女生 b ‎15‎ f 合计 c d ‎100‎ 已知在全部100名学生中随机抽取1人对创建工作满意的概率为.‎ ‎(1)在上表中a,b,c,d,e,f相应的数据依次为___________________；‎ ‎(2)是否有充足的证据说明学生对创建工作的满意情况与性别有关？‎ 解析：(1)填表如下：‎ 满意 不满意 合计 男生 ‎50‎ ‎5‎ ‎55‎ 女生 ‎30‎ ‎15‎ ‎45‎ 合计 ‎80‎ ‎20‎ ‎100‎ ‎5,30,80,20,55,45‎ ‎(2)根据列联表数据可得K2的观测值 k＝≈9.091>7.879，‎ 所以在犯错误的概率不超过0.005的前提下认为学生对创建工作的满意情况与性别有关．‎ ‎18．（12分）在5道题中有3道理科题和2道文科题．如果不放回地依次抽取2道题，求：‎ ‎(1)第1次抽到理科题的概率；‎ ‎(2)第1次和第2次都抽到理科题的概率；‎ ‎(3)在第1次抽到理科题的条件下，第2次抽到理科题的概率．‎ 解析：设“第1次抽到理科题”为事件A，“第2次抽到理科题”为事件B，则“第1次和第2次都抽到理科题”为事件AB.‎ ‎(1)从5道题中不放回地依次抽取2道题的事件数为n(Ω)＝A＝20.‎ 根据分步乘法计数原理，n(A)＝A×A＝12.‎ 于是P(A)＝＝＝…………………4分 ‎(2)因为n(AB)＝A＝6，‎ 所以P(AB)＝＝＝.…………………8分 ‎(3)方法一：由(1)(2)可得，在第1次抽到理科题的条件下，第2次抽到理科题的概率 P(B|A)＝＝＝.‎ 方法二：因为n(AB)＝6，n(A)＝12，‎ 所以P(B|A)＝＝＝.…………………12分 ‎19．(12分)某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上40件产品作为样本称出它们的质量(单位：克)．质量的分组区间为(490,495]，(495,500]，…，(510,515]，由此得到样本的频率分布直方图，如下图．‎ ‎(1)根据频率分布直方图，求质量超过505克的产品的数量；‎ ‎(2)在上述抽取的40件产品中任取2件，设Y为质量超过505克的产品数量，求Y的分布列；‎ ‎(3)从该流水线上任取5件产品，求恰有2件产品的质量超过505克的概率．‎ 解析：(1)由频率分布直方图，知质量超过505克的产品数为[(0.01＋0.05)×5]×40＝12.‎ ‎(2)依题意，得Y的所有可能取值为0,1,2.‎ P(Y＝0)＝＝，‎ P(Y＝1)＝＝，‎ P(Y＝2)＝＝.‎ ‎∴Y的分布列为 Y ‎0‎ ‎1‎ ‎2‎ P ‎(3)利用样本估计总体，该流水线上产品质量超过505克的概率为0.3.令ξ为任取的5件产品中质量超过505克的产品数量，则ξ～B(5,0.3)，故所求概率P(ξ＝2)＝C(0.3)2(0.7)3＝0.308 7.‎ ‎20．(12分)某单位为了了解用电量y(度)与气温x(℃)之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表，由表中数据得线性回归方程＝x＋，其中＝－2.现预测当气温为－4℃时，用电量的度数约为多少？‎ 用电量y(度)‎ ‎24‎ ‎34‎ ‎38‎ ‎64‎ 气温x(℃)‎ ‎18‎ ‎13‎ ‎10‎ ‎－1‎ 解析：由题意可知 ＝(18＋13＋10－1)＝10，‎ ＝(24＋34＋38＋64)＝40，＝－2.‎ 又回归方程＝－2x＋过点(10,40)，故＝60.‎ 所以当x＝－4时，＝－2×(－4)＋60＝68.‎ 故当气温为－4℃时，用电量的度数约为68度．‎ ‎21．(12分)一个商场经销某种商品，根据以往资料统计，每位顾客采用的分期付款次数ξ的分布列为：‎ ξ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ P ‎0.4‎ ‎0.2‎ ‎0.2‎ ‎0.1‎ ‎0.1‎ 商场经销一件该商品，采用1期付款，其利润为200元；采用2期或3期付款，其利润为250元；采用4期或5期付款，其利润为300元．η表示经销一件该商品的利润．‎ ‎(1)求购买该商品的3位顾客中，恰有2位采用1期付款的概率；‎ ‎(2)求η的分布列及期望E(η)．‎ 解析：(1)因为服从ξ～B(3,0.4)，运用概率公式P＝C(0.4)k(1－0.4)3－k，‎ 所以P＝C(0.4)2×(1－0.4)＝0.288.‎ ‎(2)因为采用1期付款，其利润为200元，采用2期或3期付款，其利润为250元；采用4期或5期付款，其利润为300元，η表示经销一件该商品的利润．‎ 所以可能取值为200元，250元，300元．‎ 根据表格知识得出：‎ P(η＝200)＝P(ξ＝1)＝0.4，‎ P(η＝250)＝P(ξ＝2)＋P(ξ＝3)＝0.2＋0.2＝0.4，‎ P(η＝300)＝1－P(η＝200)－P(η＝250)＝1－0.4－0.4＝0.2.‎ 故η的分布列为：‎ η ‎200‎ ‎250‎ ‎300‎ P ‎0.4‎ ‎0.4‎ ‎0.2‎ E(η)＝200×0.4＋250×0.4＋300×0.2＝240(元)．‎ ‎22．(12分)现有4个人去参加春节联欢活动，该活动有甲、乙两个项目可供参加者选择，为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢，掷出点数为1或2的人去参加甲项目联欢，掷出点数大于2的人去参加乙项目联欢．‎ ‎(1)求这4个人中恰好有2人去参加甲项目联欢的概率；‎ ‎(2)求这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率；‎ ‎(3)用X，Y分别表示这4个人中去参加甲、乙项目联欢的人数，记ξ＝|X－Y|，求随机变量ξ的分布列与数学期望E(ξ)．‎ 解析：依题意，这4个人中，每个人去参加甲项目联欢的概率为，去参加乙项目联欢的概率为.设“这4个人中恰好有i人去参加甲项目联欢”为事件Ai(i＝0,1,2,3,4)，则P(Ai)＝C()i·()4－i.‎ ‎(1)这4个人中恰好有2人去参加甲项目联欢的概率P(A2)＝C()2()2＝.‎ ‎(2)设“这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数”为事件B，则B＝A3∪A4，故P(B)＝P(A3)＋P(A4)＝C()3()＋C()4＝.‎ ‎∴这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率为.‎ ‎(3)ξ的所有可能取值为0,2,4.‎ P(ξ＝0)＝P(A2)＝，P(ξ＝2)＝P(A1)＋‎ P(A3)＝，‎ P(ξ＝4)＝P(A0)＋P(A4)＝，‎ ‎∴ξ的分布列为 ξ ‎0‎ ‎2‎ ‎4‎ P E(ξ)＝0×＋2×＋4×＝.‎