2018-2019学年内蒙古赤峰二中高二4月月考数学（文）试题 Word版

2018-2019学年内蒙古赤峰二中高二4月月考数学（文）试题 Word版

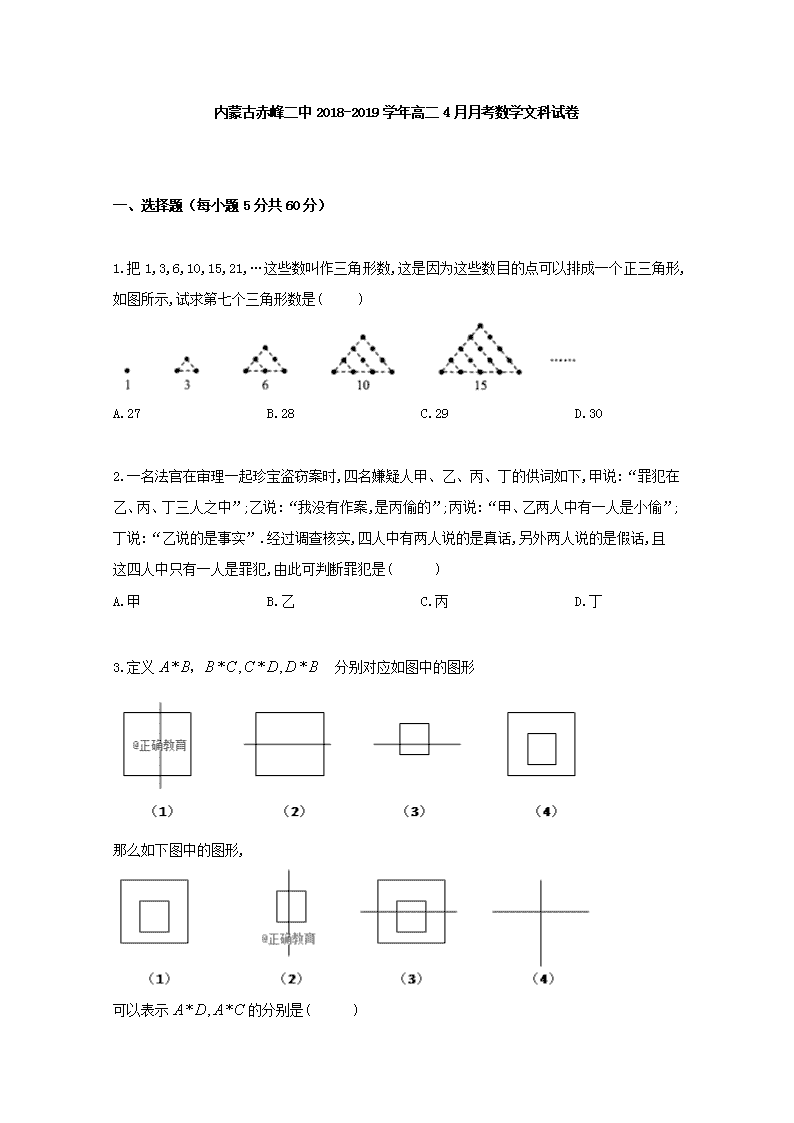
内蒙古赤峰二中2018-2019学年高二4月月考数学文科试卷 ‎ ‎ ‎ 一、选择题（每小题5分共60分）‎ ‎1.把1,3,6,10,15,21,…这些数叫作三角形数,这是因为这些数目的点可以排成一个正三角形,如图所示,试求第七个三角形数是(   )‎ A.27         B.28         C.29         D.30‎ ‎2.一名法官在审理一起珍宝盗窃案时,四名嫌疑人甲、乙、丙、丁的供词如下,甲说:“罪犯在乙、丙、丁三人之中”;乙说:“我没有作案,是丙偷的”;丙说:“甲、乙两人中有一人是小偷”;丁说:“乙说的是事实”.经过调查核实,四人中有两人说的是真话,另外两人说的是假话,且这四人中只有一人是罪犯,由此可判断罪犯是(   )‎ A.甲         B.乙         C.丙         D.丁 ‎3.定义 分别对应如图中的图形 ‎ 那么如下图中的图形, ‎ 可以表示的分别是(   )‎ A.(1),(2)     B.(2),(3)     C.(2),(4)     D.(1),(4)‎ ‎4.设复数满足 (是虚数单位),则复数在复平面内所对应的点位于(   )‎ A.第一象限     B.第二象限     C.第三象限     D.第四象限 ‎5.若复数满足 (其中是虚数单位),则的虚部为(   )‎ A 1 B i C 6 D-1‎ ‎6.复数 (为虚数单位)等于(   )‎ A. B. C. D. ‎ ‎7.已知全集,集合,则如图所示阴影区域表示的集合为(   )‎ A. ‎ B. C. D. ‎ ‎ ‎ ‎8.已知定义在上的可导函数满足：，则与的大小关系是（ ）‎ ‎(A)> (B)< ‎ ‎(C) = (D) 不确定 ‎9.已知集合,则 (   )‎ A. B. C. D. ‎ ‎10.下列命题中正确的是(   )‎ A.若为真命题,则为真命题. B.“”是“”的充要条件. C.命题“,则或”的逆否命题为“若或,则”. D.命题: ,使得,则,使得.‎ ‎11已知函数f(x)=( -m),若函数f(x)的图像在x=1处切线的斜率为3e,则f(x)的极大值是 A B C D ‎12已知函数f(x)=,则f(x)的零点可能有 A 1个 B1个或2个 C 1个或2个或3个 D2个或3个 二、填空题（每小题5分共20分）‎ ‎13命题“”的否定是__________.‎ ‎14.已知函数,则的单调递增区间为__________.‎ ‎15已知函数f(x)=lnx-ax的图像与直线x-y+1=0相切，则实数a的值为__________‎ ‎16.若函数f(x)=在（0,1）内有极小值，则实数b的取值范围为_________‎ 三、解答题 ‎17(本小题10分）‎ 设命题为上的减函数,命题:函数在 上恒成立.若为真命题, 为假命题,求的取值范围.‎ ‎18(本小题12分）‎ 为了了解我国各景点在大众中的熟知度,随机对15-65岁的人群抽样了人,回答问题“我国的“五岳”指的是哪五座名山?”,统计结果如下图表.‎ 组号 分组 回答正确的人数 回答正确的人数占本组的频率 第1组 ‎[15,25)‎ ‎0.5‎ 第2组 ‎[25,35)‎ ‎18‎ 第3组 ‎[35,45)‎ ‎0.9‎ 第4组 ‎[45,55)‎ ‎9‎ ‎0.36‎ 第5组 ‎[55,65]‎ ‎3‎ ‎ 1.分别求出的值; 2.从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人 3.在2的条件下抽取的6人中,随机抽取2人,求所抽取的人中恰好没有第3组人的概率.‎ ‎19．(本小题12分）随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了一二线城市的大街小巷.为了解共享单车在市的使用情况，某调查机构借助网络进行了问卷调查，并从参与调查的网友中抽取了200人进行抽样分析，得到表格：（单位：人）‎ 经常使用 偶尔或不用 合计 ‎30岁及以下 ‎70‎ ‎30‎ ‎100‎ ‎30岁以上 ‎60‎ ‎40‎ ‎100‎ 合计 ‎130‎ ‎70‎ ‎200‎ ‎（1）根据以上数据，能否在犯错误的概率不超过0.15的前提下认为市使用共享单车情况与年龄有关？‎ ‎（2）现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.‎ ‎（i）分别求这5人中经常使用、偶尔或不用共享单车的人数；‎ ‎（ii）从这5人中，再随机选出2人赠送一件礼品，求选出的2人中至少有1人经常使用共享单车的概率.‎ 参考公式： ，其中.‎ 参考数据：‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ 选做题，请考生在20、21两题中任选一题作答，如果多做，则按所做的第一题记分．在答题卡中把相应的题号涂黑 ‎20.[选修4—4:坐标系与参数方程](本小题12分）‎ 在平面直角坐标系中,已知曲线与曲线 (为参数).以坐标原点为极点, 轴的非负半轴为极轴建立极坐标系.‎ ‎(1).写出曲线的极坐标方程;‎ ‎(2).在极坐标系中,已知与的公共点分别为,,当时,求的值.‎ ‎21选修4－5：不等式选讲.‎ 设函数. ‎ ‎(1) 若不等式的解集为，求实数的值；‎ ‎(2) 在(1)条件下，若存在实数，使得恒成立，求实数的取值范 选做题，请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．在答题卡中把相应的题号涂黑 ‎22.[选修4-4:极坐标与参数方程](本小题12分）‎ 在直角坐标系中,圆经过伸缩变换后得到曲线.以坐标原点为极点, 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线的极坐标方程为.‎ ‎1.求曲线的直角坐标方程及直线的直角坐标方程 ‎2.设点是上一动点,求点到直线的距离的最大值，并求出此时M点的坐标 ‎23[选修4—5：不等式选讲]‎ 设， ， 均为正数，且，证明：‎ ‎(1) ≤；‎ ‎(2) ‎ ‎24.(本小题12分）‎ 设,.‎ ‎1.求的单调区间;‎ ‎2.当时,设恒成立,求实数的取值范围.‎ 高二文科数学答案 一选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B C D A B B A C B A A ‎13. 14（0,1） 15 16‎ ‎17.答案：由真,假,知与为一真一假,对进行分类讨论即可.若真,由为减函数,得当时,由不等式时取等号)知在上的最小值为 若真,则,即 若真假,则;若假真,则.综上可得 ‎18.答案：1.由频率表中第4组数据可知,第4组总人数为, 再结合频率分布直方图可知,, , , .‎ ‎2.因为第2,3,4组回答正确的人数共有54人,所以利用分层抽样在54人中抽取6人,每组分别抽取的人数为:第2组:人;第3组:人;第4组:人 .‎ ‎3.设第2组2人为:;第3组3人为:;第4组1人为:. 则从6人中随机抽取2人的所有可能的结果为:,,,,,,,,,,,,,,,共15个基本事件.其中恰好没有第3组人共3个基本事件,‎ ‎,, ∴所抽取的人中恰好没有第3组人的概率是:.‎ ‎19.答案（1）>2.072.能 (2)抽出经常用3人，不用2人 (3)‎ ‎20.答案：1.曲线的极坐标方程为,即.曲线的普通方程为, 即,所以曲线的极坐标方程为.‎ ‎2.由1知,‎ ‎ ∵ ∴ ,‎ 由,知,当,‎ ‎∴. ‎ ‎21.答案：1.由经过伸缩变换,可得曲线的方程为,‎ 即,由极坐标方程,可得直线的直角坐标方程为 2.因为椭圆的参数方程为 (为参数),所以可设点,‎ 由点到直线的距离公式,点到直线的距离为 (其中),M()由三角函数性质知,当时,点到直线的距离有最大值,此时 ‎ 21（1）a=1 (2)‎ ‎22.答案：1.,当时,,递增,‎ 当时,,递减。‎ 故的单调递增区间为,单调递减区间为。 2.,,‎ 因为设的根为, 即有,可得,, 当时,,递减。当时,,递增。‎ 所以,‎ ‎ ‎