- 2021-06-19 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届江西省新余市高三二模考试(2018
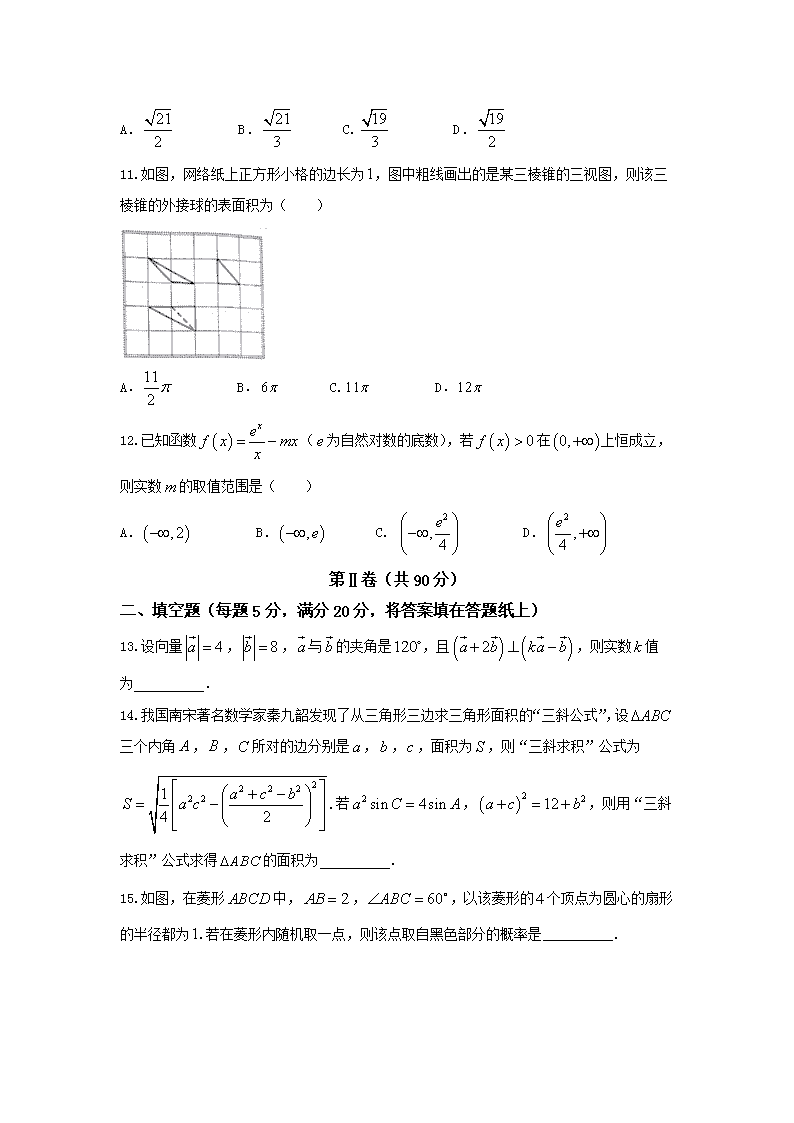
新余市2018年高三“二模”考试 数学试题卷(文科) 第Ⅰ卷(共60分) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若集合,集合,则等于( ) A. B. C. D. 2.复数的实部为( ) A. B. C. D. 3.为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为的调查样本,其中城镇户籍与农村户籍各人;男性人,女性人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( ) A.是否倾向选择生育二胎与户籍有关 B.是否倾向选择生育二胎与性别有关 C.倾向选择生育二胎的人员中,男性人数与女性人数相同 D.倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数 4.“”是“函数在区间无零点”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 5.根据如下所示的伪代码(图中箭头表示赋值语句中的“=”),可知输出的结果是( ) A. B. C. D. 6.函数的图象大致为( ) A. B. C. D. 7.过直线上的点作圆的切线,则切线长的最小值为( ) A. B. C. D. 8.已知、满足约束条件则目标函数的最小值为( ) A. B. C. D. 9.若,则实数的值为( ) A. B. C. D. 10.已知双曲线的左、右两个焦点分别为,,,为其左右顶点,以线段为直径的圆与双曲线的渐近线在第一象限的交点为,且,则双曲线的离心率为( ) A. B. C. D. 11.如图,网络纸上正方形小格的边长为,图中粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积为( ) A. B. C. D. 12.已知函数(为自然对数的底数),若在上恒成立,则实数的取值范围是( ) A. B. C. D. 第Ⅱ卷(共90分) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.设向量,,与的夹角是,且,则实数值为 . 14.我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”,设三个内角,,所对的边分别是,,,面积为,则“三斜求积”公式为.若,,则用“三斜求积”公式求得的面积为 . 15.如图,在菱形中,,,以该菱形的个顶点为圆心的扇形的半径都为.若在菱形内随机取一点,则该点取自黑色部分的概率是 . 16.已知函数若函数恰有个不同的零点,则实数的取值范围是 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知数列满足. (1)求数列的通项公式; (2)设,求数列的前项和. 18. “一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分分(分及以上为认知程度高),现从参赛者中抽取了人,按年龄分成组(第一组:,第二组:,第三组:,第四组:,第五组:),得到如图所示的频率分布直方图,已知第一组有人. (1)求; (2)求抽取的人的年龄的中位数(结果保留整数); (3)从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取人,人,人,人,人,分别记为1-5组,从这个按年龄分的组和 个按职业分的组中每组各选派人参加知识竞赛代表相应组的成绩,年龄组中1-5组的成绩分别为,,,,,职业组中1-5组的成绩分别为,,,,. (ⅰ)分别求个年龄组和个职业组成绩的平均数和方差; (ⅱ)以上述数据为依据,评价个年龄组和个职业组对“一带一路”的认知程度,并谈谈你的感想. 19. 如图,三棱柱中,平面平面,是的中点. (1)求证:平面; (2)若,,,,求三棱锥的体积. 20. 已知抛物线过点,直线过点与抛物线交于,两点.点关于轴的对称点为,连接. (1)求抛物线线的标准方程; (2)问直线是否过定点?若是,求出定点坐标;若不是,请说明理由. 21. 已知函数,. (1)讨论函数的单调区间; (2)若有两个零点,求的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程 在直角坐标系中,曲线的参数方程为(其中为参数),曲线,以坐标原点为极点,轴的在半轴为极轴建立坐标系. (1)求曲线的普通方程和曲线的极坐标方程; (2)若射线与曲线,分别交于,两点,求. 23.选修4-5:不等式选讲 已知函数. (1)若不等式的解集为,求实数的值; (2)在(1)的条件下,若存在实数使成立,求实数的取值范围. 试卷答案 一、选择题 1-5:CDCAD 6-10:BABAB 11、12:CC 二、填空题 13. 14. 15. 16. (−3/2,2) 三、解答题 17. 解:(1)当时,. 因为, ① 所以. ② ①-②得. 所以. 由于也满足上式,故. (2)由(1)得=. 所以. 故 . 18. 解:(1)根据频率分布直方图得第一组频率为, ,. (2)设中位数为,则, ,中位数为32. (3)(i)5个年龄组的平均数为, 方差为. 5个职业组的平均数为, 方差为. (ii)评价:从平均数来看两组的认知程度相同,从方差来看年龄组的认知程度更好. 19. 解法一:(Ⅰ)连结交于点,则为的中点, ∵是的中点, ∴. 又,, ∴ (Ⅱ)∵,,, ∴, ∴. 取中点,连结, ∵,, ∴为等边三角形, ∴,且, 又∵平面,平面, , ∴, ∵, ∴SC1-ABD=. 解法二:(Ⅰ)取中点,连结,,, ∵,,, ∴, ∴四边形为平行四边形, ∴, 又,, ∴. ∵, ∴四边形为平行四边形, ∴, 又,, ∴. 又, ∴平面. 又平面, ∴平面 (Ⅱ)∵, ∴, ∴. ∴, ∴. 又∵平面平面,平面平面. ∴. ∵, ∴, ∴. ∵是中点, ∴SC1-ABD= 20. 解:(1)将点代入抛物线的方程得, . 所以,抛物线的标准方程为. (2)设直线的方程为,又设,,则.由得. 则,,. 所以. 于是直线的方程为. 所以. 当时,, 所以直线过定点. 21. 解:(Ⅰ). (i)若,则当时,;当时,; 故函数在单调递减,在单调递增. (ii)当时,由,解得:或. ①若,即,则,, 故在单调递增. ②若,即,则当时,;当时,;故函数在,单调递增,在单调递减. ③若,即,则当时,;当时,;故函数在,单调递增,在单调递减. (Ⅱ)(i)当时,由(Ⅰ)知,函数在单调递减,在单调递增. ∵, 取实数满足且,则 , 所以有两个零点. (ii)若,则,故只有一个零点. (iii)若,由(I)知, 当,则在单调递增,又当时,,故不存在两个零点; 当,则函数在单调递增;在单调递减.又当时,,故不存在两个零点. 综上所述,的取值范围是. 22. 解:(Ⅰ)由得, 所以曲线的普通方程为. 把,,代入, 得, 化简得,曲线的极坐标方程为 (Ⅱ)依题意可设. 因为曲线的极坐标方程为, 将代入曲线的极坐标方程得, 解得. 同理将代入曲线的极坐标方程得. 所以 23. 解:(Ⅰ)由得,∴,即, ∴,∴. (Ⅱ)由(Ⅰ)知,令, 则, ∴的最小值为4,故实数的取值范围是.查看更多