2019届二轮复习小题满分限时练(五)作业(全国通用)
限时练(五)
(限时:45分钟)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若集合M={x|0
0)的一个焦点,则a等于( )
A.1 B. C.2 D.3
解析 ∵(,0)是双曲线的一个焦点,
∴1+a2=()2=3,∴a2=2,
又a>0,∴a=.
答案 B
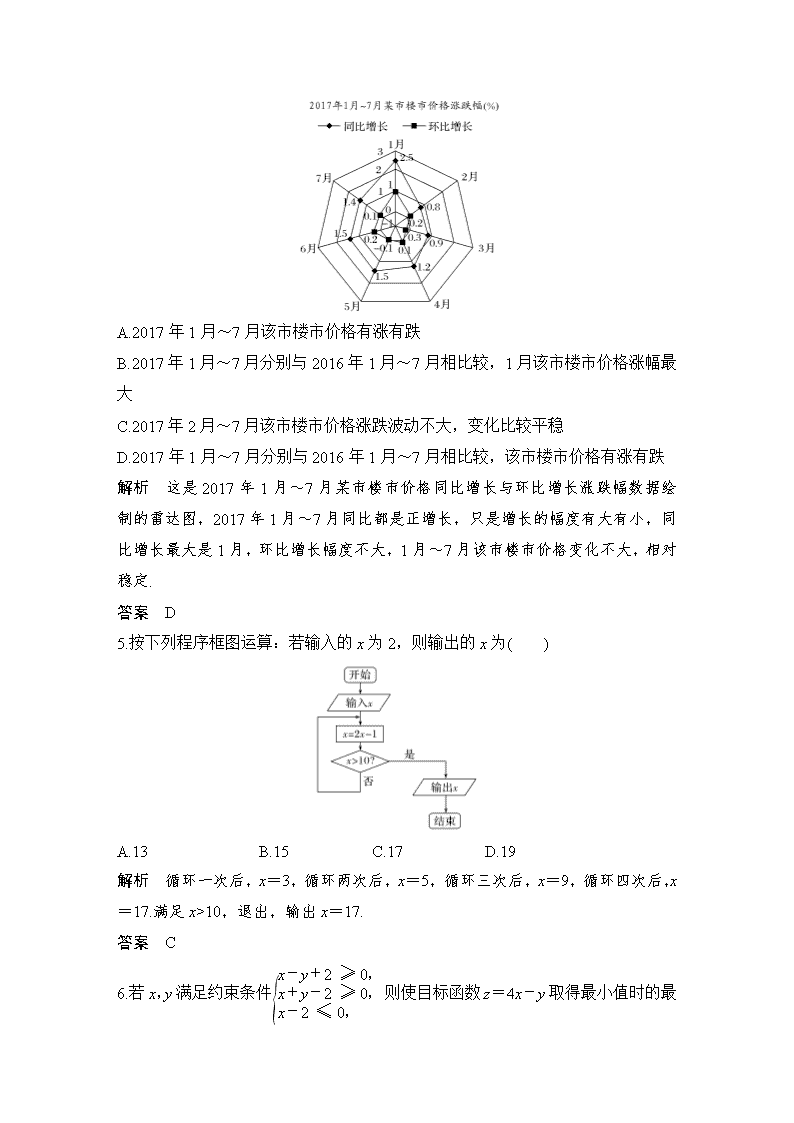
4.下图是某市统计局发布的2017年1月~7月的本市楼市价格同比增长与环比增长涨跌幅数据绘制的雷达图.(注:2017年2月与2016年2月相比较,叫同比;2017年2月与2017年1月相比较,叫环比)根据该雷达图,则下列结论错误的是( )
A.2017年1月~7月该市楼市价格有涨有跌
B.2017年1月~7月分别与2016年1月~7月相比较,1月该市楼市价格涨幅最大
C.2017年2月~7月该市楼市价格涨跌波动不大,变化比较平稳
D.2017年1月~7月分别与2016年1月~7月相比较,该市楼市价格有涨有跌
解析 这是2017年1月~7月某市楼市价格同比增长与环比增长涨跌幅数据绘制的雷达图,2017年1月~7月同比都是正增长,只是增长的幅度有大有小,同比增长最大是1月,环比增长幅度不大,1月~7月该市楼市价格变化不大,相对稳定.
答案 D
5.按下列程序框图运算:若输入的x为2,则输出的x为( )
A.13 B.15 C.17 D.19
解析 循环一次后,x=3,循环两次后,x=5,循环三次后,x=9,循环四次后,x=17.满足x>10,退出,输出x=17.
答案 C
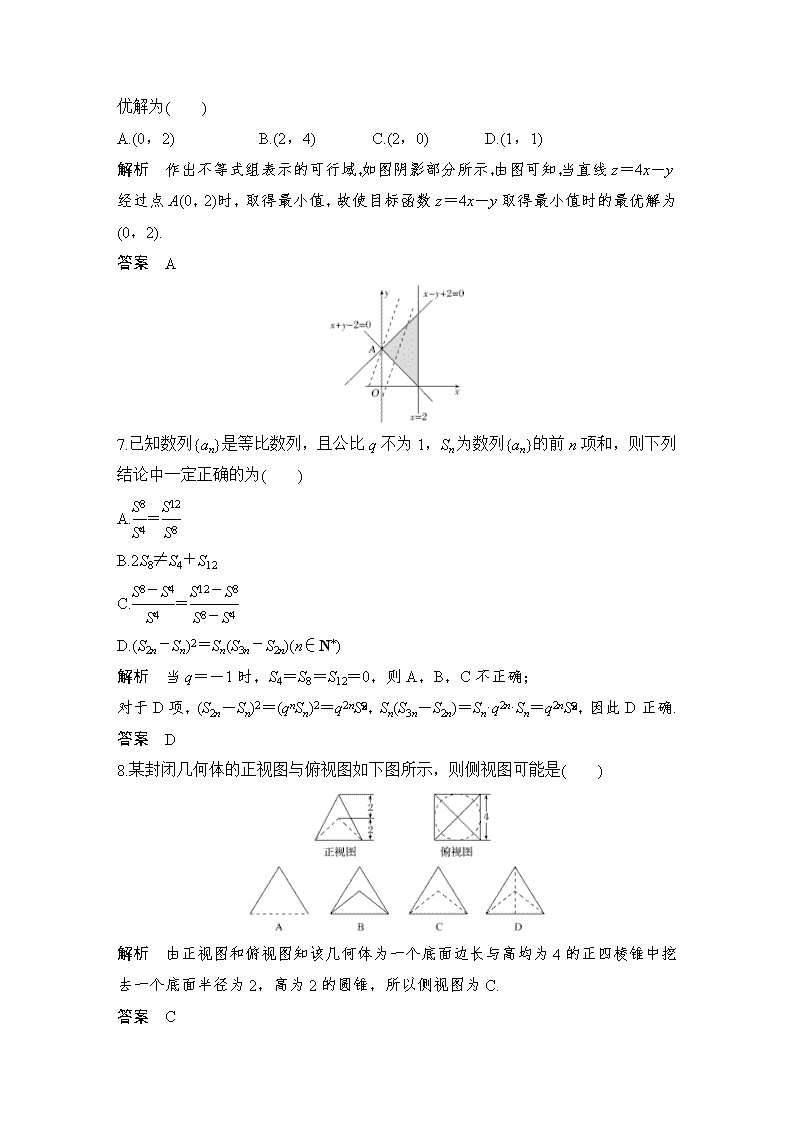
6.若x,y满足约束条件则使目标函数z=4x-y取
得最小值时的最优解为( )
A.(0,2) B.(2,4) C.(2,0) D.(1,1)
解析 作出不等式组表示的可行域,如图阴影部分所示,由图可知,当直线z=4x-y经过点A(0,2)时,取得最小值,故使目标函数z=4x-y取得最小值时的最优解为(0,2).
答案 A
7.已知数列{an}是等比数列,且公比q不为1,Sn为数列{an}的前n项和,则下列结论中一定正确的为( )
A.=
B.2S8≠S4+S12
C.=
D.(S2n-Sn)2=Sn(S3n-S2n)(n∈N*)
解析 当q=-1时,S4=S8=S12=0,则A,B,C不正确;
对于D项,(S2n-Sn)2=(qnSn)2=q2nS,Sn(S3n-S2n)=Sn·q2n·Sn=q2nS,因此D正确.
答案 D
8.某封闭几何体的正视图与俯视图如下图所示,则侧视图可能是( )
解析 由正视图和俯视图知该几何体为一个底面边长与高均为4的正四棱锥中挖去一个底面半径为2,高为2的圆锥,所以侧视图为C.
答案 C
9.在△ABC中,已知AC+BC=10,C=60°,且4ABsin A=ACsin C.若点D为AC边上一点,且AD=BD,则CD=( )
A.4 B. C.5 D.
解析 设角A,B,C的对边分别为a,b,c,则4ABsin A=ACsin C,即4csin A=bsin C,由正弦定理得,4ac=bc,∴b=4a.因为AC+BC=10,即b+a=10,所以a=2,b=8.设CD=x,则BD=8-x,由余弦定理得BD2=BC2+CD2-2BC·CD·cos C,则(8-x)2=22+x2-4x×,∴x=,∴CD=.
答案 B
10.在同一直角坐标系中,函数f(x)=sin ax(a∈R)与g(x)=(a-1)x2-ax的部分图象不可能为( )
解析 选项A对应的a=2;选项B对应的a=4;选项D对应的a=1;选项C的图象中,由f(x)=sin ax(a∈R)图象可知,a=-1,故g(x)=-2x2+x,则g(x)=(a-1)x2-ax的图象的对称轴在y轴右侧,而图中的对称轴在y轴左侧,选项C的图象不可能成立.
答案 C
11.已知F是椭圆C:+=1(a>b>0)的右焦点,P是椭圆C上动点,O为椭圆的中心,若|OP|+|PF|的取值范围是[3,5],则椭圆C的离心率为( )
A. B. C. D.
解析 设左焦点为F′,
则|OP|+|PF|=|PO|+2a-|PF′|,
又||PO|-|PF′||≤|OF′|=c.∴-c≤|PO|-|PF′|≤c,
则2a+c=5且2a-c=3,解之得a=2,c=1.
所以椭圆C的离心率e=.
答案 B
12.已知f(x)=2sin(ωx+φ)(ω>0),已知:①在(t1,t2)上不单调,且f(t1)+f(t2)=0;②∃a∈R,f-f=4,且在上单调递增,则t2-t1的最小值为( )
A. B. C. D.π
解析 由②知,f(x)的最小正周期T=×2=π,ω=2.
∴f(x)=2sin(2x+φ),
因此t2-t1的最小值为=.
答案 C
二、填空题(本大题共4个小题,每小题5分,共20分.请把正确的答案填写在各小题的横线上.)
13.函数f(x)=x2-2ln x的单调递减区间为________.
解析 函数f(x)=x2-2ln x的定义域为(0,+∞),令f′(x)=2x-=<0,得0c+d,a-b=c-d,a+c>b+d,由a-b=c-d得a-c=b-d,所以a+c+(a-c)>b+d+(b-d),a+c-(a-c)>b+d-(b-d),即a>b,c>d,因为b>c+d,所以b>c,所以a>b>c>d,所以从大到小得顺序为:甲,乙,丙,丁.
答案 甲,乙,丙,丁