数学文卷·2018届福建省晋江市永春县第一中学高二下学期期末考试（2017-07）

数学文卷·2018届福建省晋江市永春县第一中学高二下学期期末考试（2017-07）

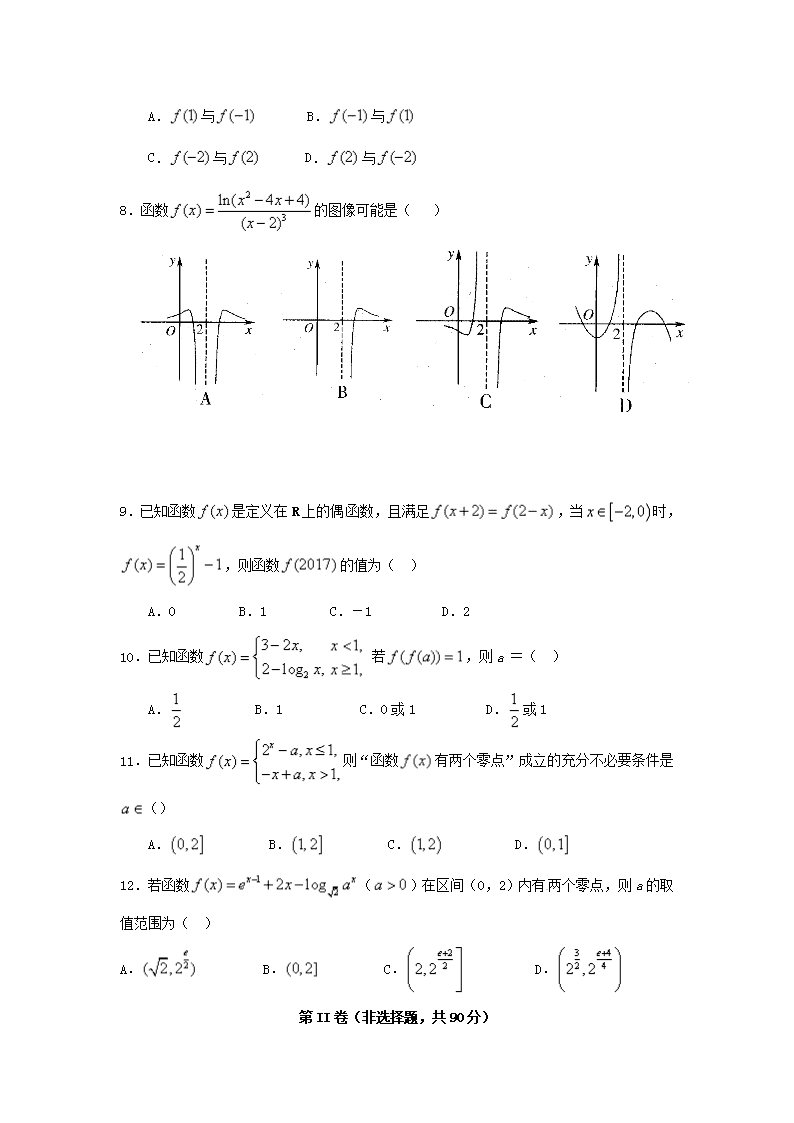
永春一中高二年（文）期末考数学科试卷 （2017.07）‎ 命题：陈志城 审核：郭文伟 考试时间：120分钟 试卷总分：150分 ‎ 第I卷（选择题，共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项 是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上。‎ ‎1．已知集合，集合，则等于（ ）‎ ‎ A． B． C． D．‎ ‎2．i是虚数单位，若（R），则的值是（ ）‎ ‎ A．－1 B．‎1 C．0 D．‎ ‎3．“为真”是“为假”的（ ）条件 ‎ A．充分不必要 B．必要不充分 C．充要 D．既不充分也不必要 ‎4．为了得到函数的图像，只需把函数的图像上所有的交点（ ）‎ A．向左平移1个单位长度，再向上平移2个单位长度 ‎ B．向右平移1个单位长度，再向上平移2个单位长度 ‎ C．向左平移1个单位长度，再向下平移2个单位长度 ‎ D．向右平移1个单位长度，再向下平移2个单位长度 ‎5．设，，则（ ）‎ ‎ A． B． C． D．‎ ‎6．已知函数的零点在区间（k∈Z），则的极大值点为（ ）‎ ‎ A．－3 B．‎0 C．－1 D．1‎ ‎7．设是一个三次函数，为其导函数，如图所示的是的图像的一部分，‎ 则的极大值与极小值分别是（）‎ A．与 B．与 ‎ C．与 D．与 ‎8．函数的图像可能是（ ）‎ ‎ ‎ ‎9．已知函数是定义在R上的偶函数，且满足，当时，，则函数的值为（ ）‎ ‎ A．0 B．‎1 C．－1 D．2‎ ‎10．已知函数 若，则a ＝（ ）‎ ‎ A． B．‎1 ‎‎ C．0或1 D．或1‎ ‎11．已知函数则“函数有两个零点”成立的充分不必要条件是（）‎ ‎ A． B． C． D．‎ ‎12．若函数（）在区间（0，2）内有两个零点，则a的取值范围为（ ）‎ A． B． C． D．‎ 第II卷（非选择题，共90分）‎ 二、填空题 ：本大题共4小题，每小题5分，共20分，请把答案填在答题卡的横线上。‎ ‎13．已知函数 则＝ ．‎ ‎14．函数图像的对称中心坐标为 ．‎ ‎15．已知角的终边经过函数经过的定点，则＝ ．‎ ‎16．若函数在（m，‎3m +1）上是单调递增函数，则实数m的取值范围为 ．‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。请在答 题卡各自题目的答题区域内作答。‎ ‎17．（本小题满分12分）‎ 已知在△ABC中内角A，B，C的对边分别为a，b，c，且．‎ ‎（Ⅰ）求角B的值；‎ ‎（Ⅱ）若△ABC的外接圆半径为1，求△ABC面积S的最大值．‎ ‎18．（本小题满分12分）‎ 已知是正项等差数列，，数列的前n项和．‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）设，，求数列的前n项和．‎ ‎19．（本小题满分12分）‎ 甲方是一农场，乙方是一工厂。由于乙方生产需占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润x（元）与年产量t（吨）满足函数关系，若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格）。‎ ‎（1）实施赔付方案后，试将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方获得最大利润的年产量；（赔付后实际年利润＝赔付前的年利润－赔付款总额）‎ ‎（2）甲方每年受乙方生产影响的经济损失金额（元），在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格s是多少？（净收入＝赔付款总额－经济损失金额）‎ ‎20．（本小题满分12分）‎ 已知A，B分别为椭圆C：（）在x轴正半轴，y轴正半轴上的顶点，原点O到直线AB的距离为，且．‎ ‎（Ⅰ）求椭圆C的离心率；‎ ‎（Ⅱ）直线l：与圆相切，并与椭圆C交于M，N两点，求，求k的值．‎ ‎21．（本小题满分12分）‎ ‎ 已知函数．‎ ‎（Ⅰ）求的单调递增区间；‎ ‎（Ⅱ）若关于x的方程有两个不同的实数解，求a的取值范围．‎ 请考生在第22、23两题中任选一题作答。注意：只能做所选定的题目。如果多做，则按所做第一个题目计分，做答时请用2B铅笔在答题卡上将所选题号后的方框涂黑。‎ ‎22．（本小题满分10分）选修4-4：坐标系与参数方程 在平面直角坐标系中xOy，已知直线l的参数方程为（t为参数，），以原点O为极点，以x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为（）．‎ ‎（Ⅰ）写出直线l的极坐标方程和曲线C的直角坐标方程；‎ ‎（Ⅱ）若直线l与曲线C相交于A，B两点，求的值．‎ ‎23．（本小题满分10分）选修4-5：不等式选讲 已知函数，．‎ ‎（Ⅰ）解不等式；‎ ‎（Ⅱ）若对任意x1∈R，都有x2∈R，使得成立，求实数a的取值范围．‎ 永春一中高二年（文）期末考数学科参考答案 （2017.07）‎ 一、选择题：（本大题共12小题，每小题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C B B C C B C C B D C D 二、填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13． 14．（0，1） 15． 16．‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。‎ 请在答题卡各自题目的答题区域内作答。‎ ‎17．‎ ‎18．‎ ‎19.‎ ‎20.‎ ‎21．解：（Ⅰ）由题意，，‎ ‎ 所以（），‎ ‎22．解：（Ⅰ）由直线的参数方程（t为参数）得 ‎23．解：（Ⅰ）由题知，，‎ 两边平方可得． （4分）‎ ‎ （Ⅱ）x1∈R，x2∈R，有，‎ 故分别求值域即可．‎ ‎，‎ ‎，故，‎ 解得或．‎ 所以a的取值范围为． （10分）‎