数学卷·2018届福建省莆田八中高二上学期第一次月考数学试卷（理科） （解析版）

数学卷·2018届福建省莆田八中高二上学期第一次月考数学试卷（理科） （解析版）

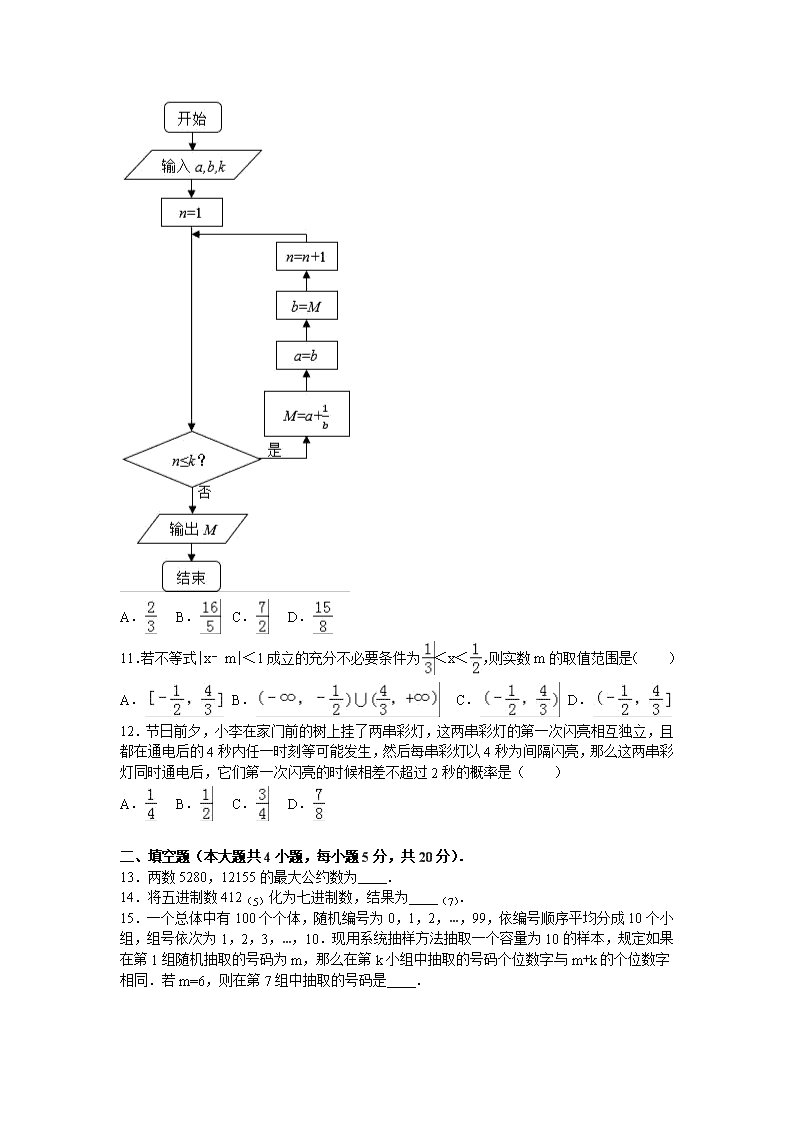
‎2016-2017学年福建省莆田八中高二（上）第一次月考数学试卷（理科）‎ ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分）．‎ ‎1．对于简单随机抽样，下列说法中正确的为（　　）‎ ‎①它要求被抽取样本的总体的个数有限，以便对其中各个个体被抽取的概率进行分析；‎ ‎②它是从总体中按排列顺序逐个地进行抽取；‎ ‎③它是一种不放回抽样；‎ ‎④它是一种等概率抽样，不仅每次从总体中抽取一个个体时，各个个体被抽取的概率相等，‎ 而且在整个抽样过程中，各个个体被抽取的概率也相等，从而保证了这种方法抽样的公平性．‎ A．①②③ B．①②④ C．①③④ D．①②③④‎ ‎2．某天，10名工人生产同一零件，生产的件数分别是16，18，15，11，16，18，18，17，15，13，设其平均数为a，中位数为b，众数为c，则有（　　）‎ A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a ‎3．由“p：8+7=16，q：π＞3”构成的复合命题，下列判断正确的是（　　）‎ A．p或q为真，p且q为假，非p为真 B．p或q为假，p且q为假，非p为真 C．p或q为真，p且q为假，非p为假 D．p或q为假，p且q为真，非p为真 ‎4．从装有黑球和白球各2个的口袋内任取2个球，那么互斥而不对立的两个事件是（　　）‎ A．至少有1个黑球，至少有1个白球 B．恰有一个黑球，恰有2个白球 C．至少有一个黑球，都是黑球 D．至少有1个黑球，都是白球 ‎5．已知x、y的一组数据如表：‎ x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎3‎ ‎4‎ ‎6‎ ‎8‎ ‎9‎ 则由表中的数据算得线性回归方程可能是（　　）‎ A． B． C． D．‎ ‎6．总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（　　）‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ A．08 B．07 C．02 D．01‎ ‎7．有下列四个命题 ‎①“若b=3，则b2=9”的逆命题； ‎ ‎②“全等三角形的面积相等”的否命题；‎ ‎③“若c≤1，则x2+2x+c=0有实根”；‎ ‎④“若A∪B=A，则A⊆B”的逆否命题．‎ 其中真命题的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎8．读程序 ‎ 其中输入甲中i=1，乙中i=1000，输出结果判断正确的是（　　）‎ A．程序不同，结果不同 B．程序相同，结果相同 C．程序相同，结果不同 D．程序不同，结果相同 ‎9．计算机中常用十六进制是逢16进1的计数制，采用数字0～9和字母A～F共16个计数符号，这些符号与十进制的数的对应关系如表：‎ ‎16进制 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ A B C D E F ‎10进制 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 例如，用十六进制表示：E+D=1B，则A×B=（　　）‎ A．6E B．72 C．5F D．B0‎ ‎10．执行如图的程序框图，若输入a，b，k分别为1，2，3，则输出的M=（　　）‎ A． B． C． D．‎ ‎11．若不等式|x﹣m|＜1成立的充分不必要条件为＜x＜，则实数m的取值范围是（　　）‎ A． B． C． D．‎ ‎12．节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时候相差不超过2秒的概率是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）．‎ ‎13．两数5280，12155的最大公约数为　　．‎ ‎14．将五进制数412（5）化为七进制数，结果为　　（7）．‎ ‎15．一个总体中有100个个体，随机编号为0，1，2，…，99，依编号顺序平均分成10个小组，组号依次为1，2，3，…，10．现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取的号码为m，那么在第k小组中抽取的号码个位数字与m+k的个位数字相同．若m=6，则在第7组中抽取的号码是　　．‎ ‎16．如图所示，已知集合A={x|框图中输出的x值}，集合B={y|框图中输出的y值}，全集U=Z．当x=﹣1时，（∁UA）∩B=　　．‎ ‎　‎ 三、解答题（本大题共6小题，共70分）．‎ ‎17．用秦九韶算法求多项式 f（x）=x6+2x5+4x3+5x2+6x+12 当x=3 时的值．‎ ‎18．甲、乙两人在相同条件下各射击10次，每次命中的环数如表：‎ 甲 ‎8‎ ‎6‎ ‎7‎ ‎8‎ ‎6‎ ‎5‎ ‎9‎ ‎10‎ ‎4‎ ‎7‎ 乙 ‎6‎ ‎7‎ ‎7‎ ‎8‎ ‎6‎ ‎7‎ ‎8‎ ‎7‎ ‎9‎ ‎5‎ ‎（1）分别计算以上两组数据的平均数；‎ ‎（2）分别计算以上两组数据的方差；‎ ‎（3）根据计算的结果，对甲乙两人的射击成绩作出评价．‎ ‎19．为了解社会对学校办学质量的满意程度，某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取6人进行问卷调查，已知高一、高二、高三的家长委员会分别有54人、1 8人、36人．‎ ‎（I）求从三个年级的家长委员会中分别应抽的家长人数；‎ ‎（Ⅱ）若从抽得的6人中随机抽取2人进行训查结果的对比，求这2人中至少有一人是高三学生家长的慨率．‎ ‎20．已知等差数列{an}满足a3=2，前3项和S3=．‎ ‎（1）求{an}的通项公式；‎ ‎（2）设等比数列{bn}满足b1=a1，b4=a15，设cn=an+bn，求{cn}的前n项和Tn．‎ ‎21．设p：实数x满足x2﹣4ax+3a2＜0，其中a＞0，q：实数x满足．‎ ‎（1）若a=1，且p∧q为真，求实数x的取值范围；‎ ‎（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．‎ ‎22．某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩（均为整数）分成六段，[40，50），[50，60），…[90，100]后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：‎ ‎（1）求第四小组的频率，并补全频率分布直方图；‎ ‎（2）估计这次考试的及格率（60分及以上为及格）和平均分；‎ ‎（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“|x﹣y|＞10”的概率．‎ ‎　‎ ‎2016-2017学年福建省莆田八中高二（上）第一次月考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分）．‎ ‎1．对于简单随机抽样，下列说法中正确的为（　　）‎ ‎①它要求被抽取样本的总体的个数有限，以便对其中各个个体被抽取的概率进行分析；‎ ‎②它是从总体中按排列顺序逐个地进行抽取；‎ ‎③它是一种不放回抽样；‎ ‎④它是一种等概率抽样，不仅每次从总体中抽取一个个体时，各个个体被抽取的概率相等，‎ 而且在整个抽样过程中，各个个体被抽取的概率也相等，从而保证了这种方法抽样的公平性．‎ A．①②③ B．①②④ C．①③④ D．①②③④‎ ‎【考点】简单随机抽样．‎ ‎【分析】根据简单随机抽样的特点，即可得出正确的结论．‎ ‎【解答】解：①简单随机抽样中被抽取样本的总体的个数有限，正确；‎ ‎②简单随机抽样是从总体中逐个地进行抽取，不正确；‎ ‎③简单随机抽样是一种不放回抽样，正确；‎ ‎④简单随机抽样是一种等可能抽样，即每个个体被抽取的可能性相等，正确．‎ 故选C．‎ ‎　‎ ‎2．某天，10名工人生产同一零件，生产的件数分别是16，18，15，11，16，18，18，17，15，13，设其平均数为a，中位数为b，众数为c，则有（　　）‎ A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a ‎【考点】众数、中位数、平均数．‎ ‎【分析】根据平均数的求法，所有数据的和除以总个数即可，中位数求法是从大到小排列后，最中间一个或两数的平均数，众数是在一组数据中出现次数最多的即是众数，根据以上方法可以确定出众数与中位数．‎ ‎【解答】解：从小到大排列此数据为：11、13、15、15、16、16、17、18、18、18．‎ 平均数为 a=（11+13+15×2+16×2+17+18×3）=15.7‎ 中位数为b是最中间两数的平均数，即b=（16+16）÷2=16；‎ 众数为c，即c=18．‎ ‎∴c＞b＞a 故选D ‎　‎ ‎3．由“p：8+7=16，q：π＞3”构成的复合命题，下列判断正确的是（　　）‎ A．p或q为真，p且q为假，非p为真 B．p或q为假，p且q为假，非p为真 C．p或q为真，p且q为假，非p为假 D．p或q为假，p且q为真，非p为真 ‎【考点】复合命题的真假．‎ ‎【分析】利用复合命题真假的判断方法判断各选项的正确性，关键要确定出两个简单命题的真假．把握非p与p的真假相反，p或q，p且q真假与p，q真假之间的关系．‎ ‎【解答】解：因为p假，q真，‎ 由复合命题的真值表可以判断，p或q为真，p且q为假，非p为真；‎ 则A正确，而BCD均错误；‎ 答案：A ‎　‎ ‎4．从装有黑球和白球各2个的口袋内任取2个球，那么互斥而不对立的两个事件是（　　）‎ A．至少有1个黑球，至少有1个白球 B．恰有一个黑球，恰有2个白球 C．至少有一个黑球，都是黑球 D．至少有1个黑球，都是白球 ‎【考点】互斥事件与对立事件．‎ ‎【分析】仔细分析每组中的两个事件所包含的基本事件，利用互斥事件和对立事件的概念逐个进行验证．‎ ‎【解答】解：对于A：事件“至少有1个黑球”和事件“至少有1个白球可以同时发生”，‎ 如一黑一白，故A不是互斥事件；‎ 对于B：事件：“恰好有一个黑球”与事件：“恰有2个白球”不能同时发生，‎ 但从口袋中任取两个球时还有可能是两个都是黑球，‎ ‎∴两个事件是互斥事件但不是对立事件，故B正确；‎ 对于C：事件：“至少有一个黑球”与事件：“都是黑球”可以同时发生，‎ 如：两个都是黑球，∴这两个事件不是互斥事件，故C不正确．‎ 对于D：事件：“至少有一个黑球”与“都是白球”不能同时发生，但一定会有一个发生，‎ ‎∴这两个事件是对立事件，故D不正确．‎ 故选B．‎ ‎　‎ ‎5．已知x、y的一组数据如表：‎ x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎3‎ ‎4‎ ‎6‎ ‎8‎ ‎9‎ 则由表中的数据算得线性回归方程可能是（　　）‎ A． B． C． D．‎ ‎【考点】线性回归方程．‎ ‎【分析】求出，，代入线性回归方程，可得B满足，即可得出结论．‎ ‎【解答】解：由题意， =（2+3+4+5+6）=4，‎ ‎=（3+4+6+8+9）=6，‎ 代入线性回归方程，可得 A不满足；‎ B满足；‎ C满足；‎ D不满足，‎ 又由x、y为正相关关系，‎ 故选：B．‎ ‎　‎ ‎6．总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（　　）‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ A．08 B．07 C．02 D．01‎ ‎【考点】简单随机抽样．‎ ‎【分析】从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读，依次为65，72，08，02，63，14，07，02，43，69，97，28，01，98，…，其中08，02，14，07，01符合条件，故可得结论．‎ ‎【解答】解：从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读，‎ 第一个数为65，不符合条件，第二个数为72，不符合条件，‎ 第三个数为08，符合条件，‎ 以下符合条件依次为：08，02，14，07，01，‎ 故第5个数为01．‎ 故选：D．‎ ‎　‎ ‎7．有下列四个命题 ‎①“若b=3，则b2=9”的逆命题； ‎ ‎②“全等三角形的面积相等”的否命题；‎ ‎③“若c≤1，则x2+2x+c=0有实根”；‎ ‎④“若A∪B=A，则A⊆B”的逆否命题．‎ 其中真命题的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】写出其逆命题，可判断①；写出否命题，举例即可判断②；由二次方程的判别式的符号，即可判断③‎ 由集合的运算性质：A∪B=A，则A⊆B，即可判断原命题的真假，再由互为逆否命题的两命题的等价性，可判断④．‎ ‎【解答】解：①“若b=3，则b2=9”的逆命题是“若b2=9，则b=3”，显然错的；‎ ‎②“全等三角形的面积相等”的否命题是“不全等的三角形，其面积不相等”，‎ 比如同底等高的三角形，面积相等，故②错；‎ ‎③方程x2+2x+c=0的判别式为△=4﹣4c，若c≤1，则△≥0，故③对；‎ ‎④若A∪B=A，则B⊆A，则命题“若A∪B=A，则A⊆B”为假命题，由逆否命题的等价性 可知其逆否命题也为假命题．‎ 故选A．‎ ‎　‎ ‎8．读程序 ‎ 其中输入甲中i=1，乙中i=1000，输出结果判断正确的是（　　）‎ A．程序不同，结果不同 B．程序相同，结果相同 C．程序相同，结果不同 D．程序不同，结果相同 ‎【考点】伪代码．‎ ‎【分析】程序甲是WHILE WEND语句，只要变量i≤1000成立，求和运算就要执行下去，直到i＞1000时终止运算并输出求出的和S；而程序乙是DO LOOP UNTIL语句，只要变量i≥1成立，求和运算就要执行下去，直到i＜1时终止运算并输出求出的和S，由此可得两程序结构不同，但输出的S相同，可得本题答案．‎ ‎【解答】解：程序甲中，计数变量i从1开始逐步递增，每次增加1，直到i=1000时终止，‎ 累加变量从0开始，这个程序计算的是：1+2+3+…+1000，‎ 程序乙中，计数变量从1000开始逐步递减，每次减少1，直到i=1时终止，‎ 累加变量从0开始，这个程序计算的是1000+19+…+3+2+1，‎ 由此可得，这两个程序是不同的，但运算的结果都是：S=1+2+3+…+1000=500500．‎ 故选D．‎ ‎　‎ ‎9．计算机中常用十六进制是逢16进1的计数制，采用数字0～9和字母A～F共16个计数符号，这些符号与十进制的数的对应关系如表：‎ ‎16进制 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ A B C D E F ‎10进制 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 例如，用十六进制表示：E+D=1B，则A×B=（　　）‎ A．6E B．72 C．5F D．B0‎ ‎【考点】根据实际问题选择函数类型．‎ ‎【分析】先算出十进制下的结果，再由进位制下转换的规则转换．‎ ‎【解答】解：由表，10×11=110，‎ ‎110÷16商是6余数是14，‎ 故A×B=6E 应选A．‎ ‎　‎ ‎10．执行如图的程序框图，若输入a，b，k分别为1，2，3，则输出的M=（　　）‎ A． B． C． D．‎ ‎【考点】程序框图．‎ ‎【分析】模拟执行程序，依次写出每次循环得到的a，b，k的值，当M=时满足条件n≤k，退出循环，输出M的值．‎ ‎【解答】解：n=1时，M=1+=，‎ n=2时，M=2+=，‎ n=3时，M=+=，‎ 故选：D．‎ ‎　‎ ‎11．若不等式|x﹣m|＜1成立的充分不必要条件为＜x＜，则实数m的取值范围是（　　）‎ A． B． C． D．‎ ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】由题意得得出m的取值范围．‎ ‎【解答】解：∵|x﹣m|＜1，∴m﹣1＜x＜m+1‎ ‎∵不等式|x﹣m|＜1的充分不必要条件是“”，‎ 由题意得得，‎ 故选：A．‎ ‎　‎ ‎12．节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时候相差不超过2秒的概率是（　　）‎ A． B． C． D．‎ ‎【考点】几何概型．‎ ‎【分析】设两串彩灯第一次闪亮的时刻分别为x，y，由题意可得0≤x≤4，0≤y≤4，要满足条件须|x﹣y|≤2，作出其对应的平面区域，由几何概型可得答案．‎ ‎【解答】解：设两串彩灯第一次闪亮的时刻分别为x，y，‎ 由题意可得0≤x≤4，0≤y≤4，‎ 它们第一次闪亮的时候相差不超过2秒，则|x﹣y|≤2，‎ 由几何概型可得所求概率为上述两平面区域的面积之比，‎ 由图可知所求的概率为： =‎ 故选C ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分）．‎ ‎13．两数5280，12155的最大公约数为　55　．‎ ‎【考点】辗转相除法．‎ ‎【分析】利用辗转相除法即可得出．‎ ‎【解答】解：12155=5280×2+1595，5280=1595×3+495，1595=495×3+110，495=110×4+55，110=55×2．‎ ‎∴两数5280，12155的最大公约数为55．‎ 故答案为：55．‎ ‎　‎ ‎14．将五进制数412（5）化为七进制数，结果为　212　（7）．‎ ‎【考点】整除的定义．‎ ‎【分析】首先把五进制数化为十进制数，然后再把十进制数化为七进制数即可．‎ ‎【解答】解：412（5）=4×52+1×51+2×50=107‎ 把十进制的107化为七进制：‎ ‎107÷7=15…2，‎ ‎15÷7=2…1，‎ ‎2÷7=0…2，‎ 所以结果是212（7）‎ 故答案为：212．‎ ‎　‎ ‎15．一个总体中有100个个体，随机编号为0，1，2，…，99，依编号顺序平均分成10个小组，组号依次为1，2，3，…，10．现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取的号码为m，那么在第k小组中抽取的号码个位数字与m+k的个位数字相同．若m=6，则在第7组中抽取的号码是　63　．‎ ‎【考点】系统抽样方法．‎ ‎【分析】此问题总体中个体的个数较多，因此采用系统抽样．按题目中要求的规则抽取即可，在第k小组中抽取的号码个位数字与m+k的个位数字相同，由m=6，k=7得到要抽数字的个位数．‎ ‎【解答】解：∵m=6，k=7，m+k=13，‎ ‎∴在第7小组中抽取的号码是63．‎ 故答案为：63．‎ ‎　‎ ‎16．如图所示，已知集合A={x|框图中输出的x值}，集合B={y|框图中输出的y值}，全集U=Z．当x=﹣1时，（∁UA）∩B=　{﹣3，﹣1，7，9}　．‎ ‎【考点】程序框图．‎ ‎【分析】利用函数关系y=2x﹣1，初始值x=﹣1，…，x=6时停止循环，可得A，B，即可得出．‎ ‎【解答】解：经过第一次循环输出y=﹣3，x=0‎ 经过第二次循环输出y=﹣1，x=1‎ 经过第三次循环输出y=1，x=2‎ 经过第四次循环输出y=3，x=3‎ 经过第五次循环输出y=5，x=4‎ 经过第六次循环输出y=7，x=5‎ 经过第七次循环输出y=9，x=6结束循环 所以A={0，1，2，3，4，5，6}； B={﹣3，﹣1，1，3，5，7，9}‎ ‎（CUA）∩B={﹣3，﹣1，7，9}．‎ 故答案为：{﹣3，﹣1，7，9}．‎ ‎　‎ 三、解答题（本大题共6小题，共70分）．‎ ‎17．用秦九韶算法求多项式 f（x）=x6+2x5+4x3+5x2+6x+12 当x=3 时的值．‎ ‎【考点】秦九韶算法．‎ ‎【分析】利用秦九韶算法计算多项式的值，先将多项式转化为x（x（x（x（x（x+2）+4）+5）+6）+12的形式，然后逐步计算v0至v5的值，即可得到答案．‎ ‎【解答】解：f（x）=x6+2x5+4x3+5x2+6x+12 ‎ ‎=x（x（x（x（x（x+2）+4）+5）+6）+12‎ 则v0=1‎ v1=5‎ v2=19‎ v3=62‎ v4=194‎ v5=588‎ 故多项式当x=2时f（x）=588．‎ ‎　‎ ‎18．甲、乙两人在相同条件下各射击10次，每次命中的环数如表：‎ 甲 ‎8‎ ‎6‎ ‎7‎ ‎8‎ ‎6‎ ‎5‎ ‎9‎ ‎10‎ ‎4‎ ‎7‎ 乙 ‎6‎ ‎7‎ ‎7‎ ‎8‎ ‎6‎ ‎7‎ ‎8‎ ‎7‎ ‎9‎ ‎5‎ ‎（1）分别计算以上两组数据的平均数；‎ ‎（2）分别计算以上两组数据的方差；‎ ‎（3）根据计算的结果，对甲乙两人的射击成绩作出评价．‎ ‎【考点】极差、方差与标准差；众数、中位数、平均数．‎ ‎【分析】（1）根据平均数的计算公式求出平均数即可；‎ ‎（2）根据方差的计算公式求出方差即可；‎ ‎（3）根据（1），（2）判断即可．‎ ‎【解答】解：（1）甲的平均分为： ==7；‎ 乙的平均分为： ==7 …‎ ‎（2）甲的方差为： = [（8﹣7）2+（6﹣7）2+…+（7﹣7）2]=3；‎ 乙的方差为： = [（6﹣7）2+（7﹣7）2+…+（5﹣7）2]=1.2 …‎ ‎（3）甲、乙的平均分相同，说明甲、乙两人射击的平均水平相当，又＞，‎ 说明乙的射击水平要比甲的射击水平更稳定．…‎ ‎　‎ ‎19．为了解社会对学校办学质量的满意程度，某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取6人进行问卷调查，已知高一、高二、高三的家长委员会分别有54人、1 8人、36人．‎ ‎（I）求从三个年级的家长委员会中分别应抽的家长人数；‎ ‎（Ⅱ）若从抽得的6人中随机抽取2人进行训查结果的对比，求这2人中至少有一人是高三学生家长的慨率．‎ ‎【考点】概率的应用．‎ ‎【分析】（I）由题意知总体个数是54+18+36，要抽取的个数是6，做出每个个体被抽到的概率，分别用三个年级的数目乘以概率，得到每一个年级要抽取的人数．‎ ‎（II）本题为古典概型，先将各区所抽取的家长用字母表达，分别计算从抽取的6个家长中随机抽取2个的个数和至少有1个来自高三的个数，再求比值即可．‎ ‎【解答】解：（I）家长委员会总数为54+18+36=108，‎ 样本容量与总体中的个体数比为，‎ 所以从三个年级的家长委员会中分别应抽的家长人数为3，1，2．‎ ‎（II）设A1，A2，A3为从高一抽得的3个家长，‎ B1为从高二抽得的1个家长，‎ C1，C2为从高三抽得的2个家长，‎ 从抽得的6人中随机抽取2人，‎ 全部的可能结果有：C62=15种，‎ 这2人中至少有一人是高三学生家长的结果有 ‎（A1，C1），（A1，C2），（A2，C1），（A2，C2），（A3，C1），（A3，C2），‎ ‎（B1，C1），（B1，C2），（C1，C2），一共有9种．‎ 所以所求的概率为．‎ ‎　‎ ‎20．已知等差数列{an}满足a3=2，前3项和S3=．‎ ‎（1）求{an}的通项公式；‎ ‎（2）设等比数列{bn}满足b1=a1，b4=a15，设cn=an+bn，求{cn}的前n项和Tn．‎ ‎【考点】数列的求和；数列递推式．‎ ‎【分析】（1）利用等差数列的通项公式与求和公式即可得出．‎ ‎（2）利用等差数列与等比数列的求和公式即可得出．‎ ‎【解答】解：（1）设{an}的公差为d，则由已知条件得 a1+2d=2，3a1+d=，‎ 化简得a1+2d=2，a1+d=，解得a1=1，d=，‎ 故{an}的通项公式an=1+，即an=．‎ ‎（2）由（1）得b1=1，b4=a15==8．设{bn}的公比为q，则q3==8，从而q=2，‎ 故{bn}的前n项和 Sn==2n﹣1．‎ ‎{cn}的前n项和Tn=+2n﹣1=+2n﹣1．‎ ‎　‎ ‎21．设p：实数x满足x2﹣4ax+3a2＜0，其中a＞0，q：实数x满足．‎ ‎（1）若a=1，且p∧q为真，求实数x的取值范围；‎ ‎（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．‎ ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】（1）若a=1，且p∧q为真，则p，q同时为真，即可求实数x的取值范围；‎ ‎（2）根据充分条件和必要条件的关系即可得到结论．‎ ‎【解答】解：（1）由x2﹣4ax+3a2＜0，得（x﹣3a）（x﹣a）＜0．又a＞0，‎ 所以a＜x＜3a．‎ 当a=1时，1＜x＜3，即p为真时实数x的取值范围是1＜x＜3．…‎ 由，‎ 得2＜x≤3，‎ 即q为真时实数x的取值范围是2＜x≤3．…‎ 若p∧q为真，则p真且q真，…‎ 所以实数x的取值范围是2＜x＜3．…‎ ‎（2）￢p是￢q的充分不必要条件，即￢p⇒￢q，且￢q推不出￢p．‎ 即q是p的充分不必要条件，‎ 则，解得1＜a≤2，‎ 所以实数a的取值范围是1＜a≤2．…‎ ‎　‎ ‎22．某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩（均为整数）分成六段，[40，50），[50，60），…[90，100]后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：‎ ‎（1）求第四小组的频率，并补全频率分布直方图；‎ ‎（2）估计这次考试的及格率（60分及以上为及格）和平均分；‎ ‎（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“|x﹣y|＞10”的概率．‎ ‎【考点】古典概型及其概率计算公式；茎叶图．‎ ‎【分析】（1）由频率分布的直方图可得，第四小组的频率等于1减去其它小组的频率，第四个小矩形的高等于频率除以组距．‎ ‎（2）这次考试的及格的频率等于60分以上各个组的频率之和，此值即为及格的概率．用各个组的平均值乘以该组的频率，即得所求的平均分．‎ ‎（3）由频率分步直方图可得，成绩是40～50分的有4人，90～100分的学生有2人，满足“|x﹣y|＞10”的选法有 4×2=8种，而所有的取法有 =15种，由此求得“|x﹣y|＞10”的概率．‎ ‎【解答】解：（1）由频率分布的直方图可得，第四小组的频率为 1﹣10（0.01+0.015+0.015+0.025+0.05）=0.3．‎ 故第四个小矩形的高为=0.03．如图所示：‎ ‎（2）由于这次考试的及格的频率为10×（0.015+0.03+0.025+0.005）=0.75，故及格率为0.75．‎ 由频率分布直方图可得平均分为 0.1×45+0.15×55+0.15×65+0.3×75+0.25×85+0.05×95=71．‎ ‎（3）由频率分步直方图可得，成绩是40～50分的有40×0.1=4人，90～100分的学生有40×0.05=2人，记取出的2个人的成绩为x，y，‎ ‎“|x﹣y|＞10”说明选出的2个人一个成绩在[40，50）内，另一个在[50，60）内，‎ 故满足“|x﹣y|＞10”的选法有 4×2=8种，而所有的取法有 =15种，‎ 故满足“|x﹣y|＞10”的概率等于．‎ ‎　‎