- 2021-06-19 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
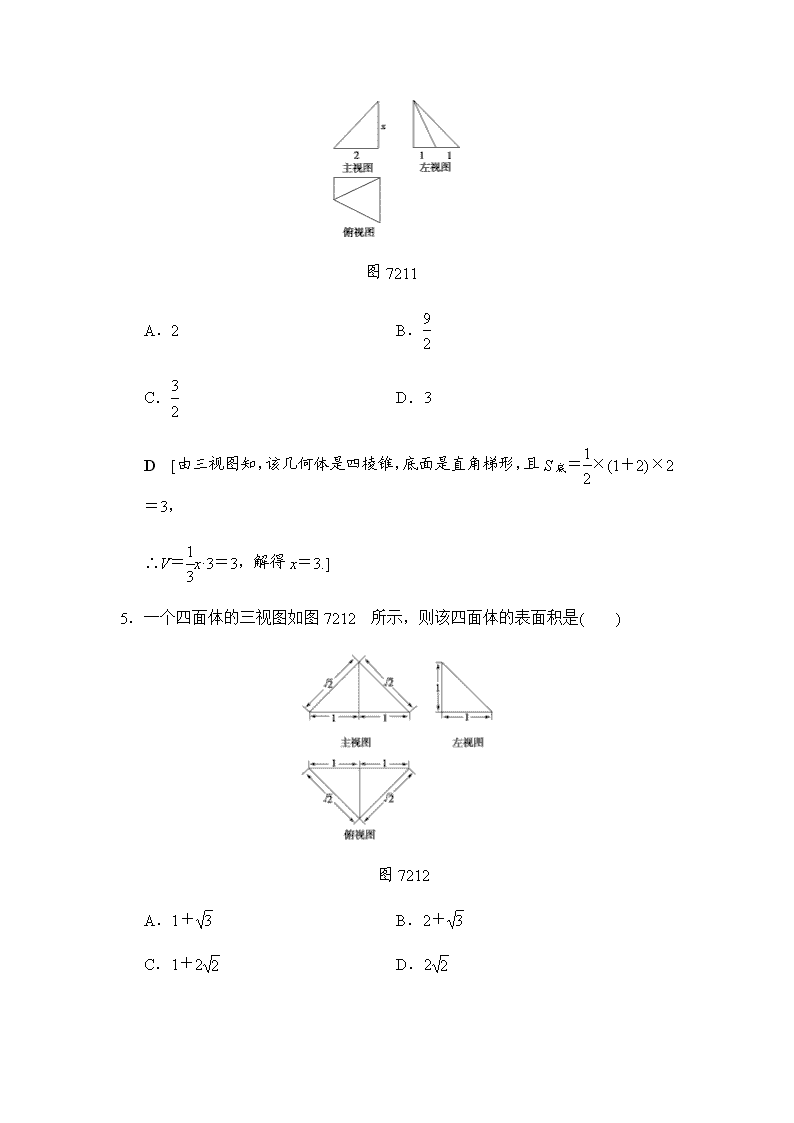
2019高三数学文北师大版一轮课时分层训练37+简单几何体的表面积与体积
课时分层训练(三十七) 简单几何体的表面积与体积 (对应学生用书第 252 页) A 组 基础达标 (建议用时:30 分钟) 一、选择题 1.已知等腰直角三角形的直角边的长为 2,将该三角形绕其斜边所在的直线旋 转一周而形成的曲面所围成的几何体的体积为( ) A.2 2π 3 B.4 2π 3 C.2 2π D.4 2π B [依题意知,该几何体是以 2为底面半径, 2为高的两个同底圆锥组成的 组合体,则其体积 V=1 3π( 2)2×2 2=4 2 3 π.] 2.已知底面边长为 1,侧棱长为 2的正四棱柱的各顶点均在同一个球面上,则 该球的体积为( ) A.32π 3 B.4π C.2π D.4π 3 D [依题意可知正四棱柱体对角线的长度等于球的直径,可设球半径为 R, 则 2R= 12+12+( 2)2=2,解得 R=1,所以 V=4π 3 R3=4π 3 .] 3.(2017·浙江高考)某几何体的三视图如图 7210 所示(单位:cm),则该几何体 的体积(单位:cm3)是( ) 【导学号:00090237】 图 7210 A.π 2 +1 B.π 2 +3 C.3π 2 +1 D.3π 2 +3 A [由几何体的三视图可知,该几何体是一个底面半径为 1,高为 3 的圆锥 的一半与一个底面为直角边长是 2的等腰直角三角形,高为 3 的三棱锥的组 合体, ∴该几何体的体积 V=1 3 ×1 2π×12×3+1 3 ×1 2 × 2× 2×3=π 2 +1. 故选 A.] 4.某几何体的三视图如图 7211 所示,且该几何体的体积是 3,则主视图中的 x 的值是( ) 图 7211 A.2 B.9 2 C.3 2 D.3 D [由三视图知,该几何体是四棱锥,底面是直角梯形,且 S 底=1 2 ×(1+2)×2 =3, ∴V=1 3x·3=3,解得 x=3.] 5.一个四面体的三视图如图 7212 所示,则该四面体的表面积是( ) 图 7212 A.1+ 3 B.2+ 3 C.1+2 2 D.2 2 B [四面体的直观图如图所示.侧面 SAC⊥底面 ABC, 且△SAC 与△ABC 均为腰长是 2的等腰直角三角形, SA=SC=AB=BC= 2,AC=2. 设 AC 的中点为 O,连接 SO,BO,则 SO⊥AC, ∴SO⊥平面 ABC,∴SO⊥BO. 又 OS=OB=1,∴SB= 2, 故△SAB 与△SBC 均是边长为 2的正三角形,故该四面体的表面积为 2×1 2 × 2× 2+2× 3 4 ×( 2)2=2+ 3.] 二、填空题 6.现有橡皮泥制作的底面半径为 5、高为 4 的圆锥和底面半径为 2,高为 8 的圆 柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的 新的圆锥和圆柱各一个,则新的底面半径为______. 7 [设新的底面半径为 r,由题意得 1 3 ×π×52×4+π×22×8=1 3 ×π×r2×4+π×r2×8, ∴r2=7,∴r= 7.] 7.一个六棱锥的体积为 2 3,其底面是边长为 2 的正六边形,侧棱长都相等, 则该六棱锥的侧面积为________. 【导学号:00090238】 12 [设正六棱锥的高为 h,棱锥的斜高为 h′. 由题意,得1 3 ×6×1 2 ×2× 3×h=2 3, ∴h=1, ∴斜高 h′= 12+( 3)2=2, ∴S 侧=6×1 2 ×2×2=12.] 8.某几何体的三视图如图 7213 所示,则该几何体的体积为________. 图 7213 13 6 π [由三视图可知,该几何体是一个圆柱和半个圆锥组合而成的几何体, 其体积为 π×12×2+1 2 ×1 3π×12×1=13 6 π.] 三、解答题 9.(2018·福州模拟)已知底面为正方形的四棱锥 PABCD,如图(1)所示,PC⊥平 面 ABCD,其中图(2)为该四棱锥的主视图和左视图,它们是腰长为 4 cm 的全 等的等腰直角三角形. (1)根据图(2)所给的主视图、左视图,画出相应的俯视图,并求出该俯视图的 面积; (2)求四棱锥 PABCD 的侧面积. 图 7214 [解] (1)该四棱锥的俯视图为内含一条对角线,边长为 4 cm 的正方形,俯视 图如图所示,其面积为 16 cm2 (2)侧面积为 2×1 2 ×4×4+2×1 2 ×4×4 2=16+16 2 10.如图 7215,从正方体 ABCDA1B1C1D1 的 8 个顶点中选出的 4 个点恰为一 个正四面体的顶点. 图 7215 (1)若选出 4 个顶点包含点 A,请在图中画出这个正四面体; (2)求棱长为 a 的正四面体外接球的半径. [解] (1)如图所示,选取的四个点分别为 A,D1,B1,C. (2)棱长为 a 的正四面体外接球的半径等于正方体外接球的半径等于正方体对 角线长的一半,因为正四面体的棱长 a,所以正方体的边长为 2 2 a,因此外接 球的半径为 3 2 × 2 2 a= 6 4 A. B 组 能力提升 (建议用时:15 分钟) 1.(2015·全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为 r)组成一个几何 体,该几何体三视图中的主视图和俯视图如图 7216 所示.若该几何体的表 面积为 16+20π,则 r=( ) 图 7216 A.1 B.2 C.4 D.8 B [如图,该几何体是一个半球与一个半圆柱的组合 体,球的半径为 r,圆柱的底面半径为 r,高为 2r,则 表面积 S=1 2 ×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又 S= 16+20π,∴(5π+4)r2=16+20π,∴r2=4,r=2,故选 B.] 2.(2018·赣州模拟)在四面体 SABC 中,SA⊥平面 ABC,∠ABC=90°,SA=AC= 2,AB=1,则该四面体的外接球的表面积为________. 【导学号:00090239】 8π [设四面体 SABC 的外接球的半径为 r,四面体 SABC 可看成如图所示的 长方体的一部分,则四面体的外接球的球心为 SC 的中点,∴2r=SC= SA2+AC2= 22+22=2 2,∴r= 2,∴该四面体的外接球的表面积 S=8π. ] 3.一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点 和底面圆周都在这个球面上,如图 7217,已知圆锥底面面积是这个球面面 积的 3 16 ,设球的半径为 R,圆锥底面半径为 r. (1)试确定 R 与 r 的关系,并求出较大圆锥与较小圆锥的体积之比; (2)求出两个圆锥的体积之和与球的体积之比. 图 7217 [解] (1)不妨设球的半径为 4; 则球的表面积为 64π,圆锥的底面积为 12π, ∴圆锥的底面半径为 2 3; 由几何体的特征知球心到圆锥底面的距离,球的半径以及圆锥底面的半径三 者可以构成一个直角三角形 由此可以求得球心到圆锥底面的距离是 42-(2 3)2=2, 所以圆锥体积较小者的高为 4-2=2, 同理可得圆锥体积较大者的高为 4+2=6; 又由这两个圆锥的底面相同, ∴较大圆锥与较小圆锥的体积之比等于它们高之比,即 3∶1 (2)由(1)可得两个圆锥的体积和为1 3·π·(2 3)2·8=32π, 球的体积为4 3·π·43=256 3 π, 故两个圆锥的体积之和与球的体积之比为 32π∶256 3 π=3∶8查看更多