- 2021-06-19 发布 |
- 37.5 KB |
- 13页

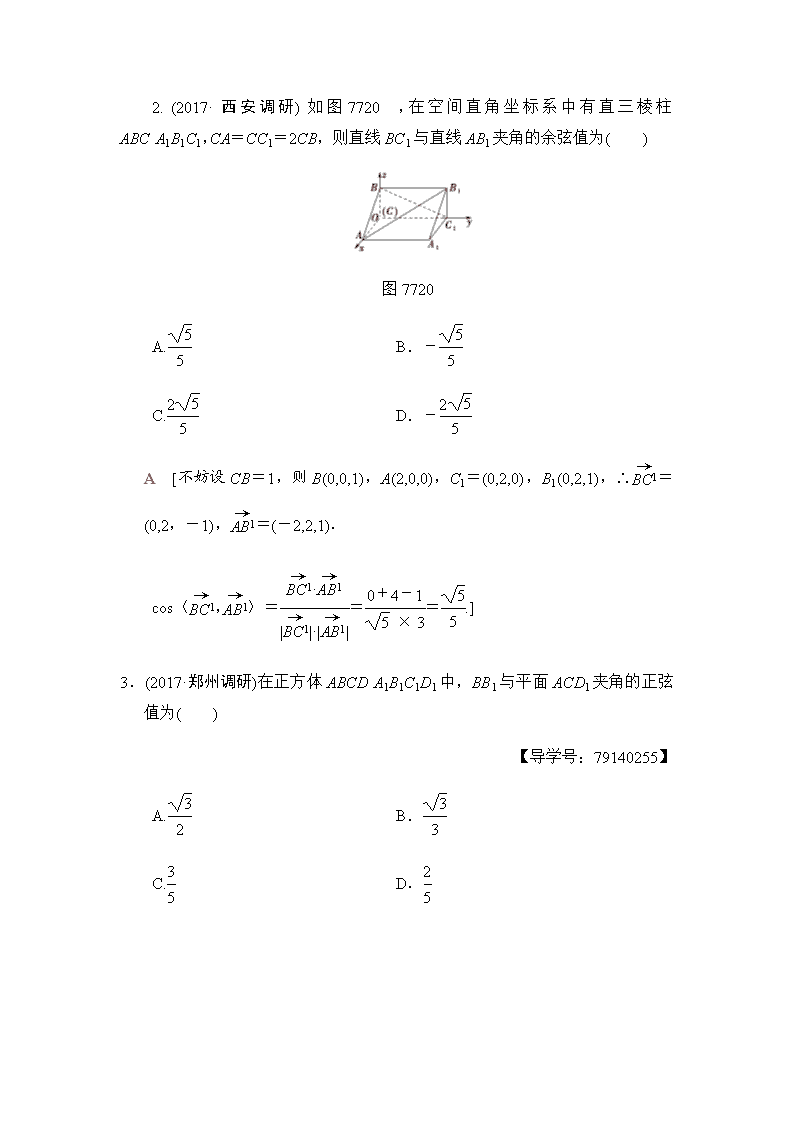

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019高三数学理北师大版一轮课时分层训练47 利用空间向量求空间角
课时分层训练(四十七) 利用空间向量求空间角 (对应学生用书第291页) A组 基础达标 一、选择题 1.在正方体A1B1C1D1ABCD中,AC与B1D夹角的大小为( ) A. B. C. D. D [建立如图所示的空间直角坐标系,设正方体边长为1,则A(0,0,0),C(1,1,0),B1(1,0,1),D(0,1,0). ∴=(1,1,0), =(-1,1,-1), ∵·=1×(-1)+1×1+0×(-1)=0, ∴⊥, ∴AC与B1D的夹角为.] 2. (2017·西安调研)如图7720,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( ) 图7720 A. B.- C. D.- A [不妨设CB=1,则B(0,0,1),A(2,0,0),C1=(0,2,0),B1(0,2,1),∴=(0,2,-1),=(-2,2,1). cos〈,〉===.] 3.(2017·郑州调研)在正方体ABCDA1B1C1D1中,BB1与平面ACD1夹角的正弦值为( ) 【导学号:79140255】 A. B. C. D. B [设正方体的棱长为1,以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图所示.则B(1,1,0),B1(1,1,1),A(1,0,0),C(0,1,0),D1(0,0,1), 所以1=(0,0,1),=(-1,1,0),1=(-1,0,1). 令平面ACD1的法向量为n=(x,y,z),则n·=-x+y=0,n·1=-x+z=0,令x=1,可得n=(1,1,1),所以sin θ=|cos〈n,1〉|==.] 4.已知正三棱柱ABCA1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1夹角的正弦值等于( ) A. B. C. D. A [ 如图所示建立空间直角坐标系,设正三棱柱的棱长为2,则O(0,0,0),B(,0,0),A(0,-1,0),B1(,0,2),所以=(,1,2),由题知=(-,0,0)为侧面ACC1A1的法向量.即sin θ==.故选A.] 5.在正方体ABCDA1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD 所成的锐二面角的余弦值为( ) A. B. C. D. B [以A为原点建立如图所示的空间直角坐标系Axyz,设棱长为1,则A1(0,0,1), E,D(0,1,0),∴=(0,1,-1),=. 设平面A1ED的一个法向量为n1=(1,y,z), ∴有即 解得 ∴n1=(1,2,2). ∵平面ABCD的一个法向量为n2=(0,0,1). ∴cos〈n1,n2〉==, 即所成的锐二面角的余弦值为.] 二、填空题 6.在长方体ABCDA1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1夹角的正弦值为________. [ 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设n=(x,y,z)为平面A1BC1的法向量, 则n·=0,n·=0, 即令z=2,则y=1,x=2, 于是n=(2,1,2),=(0,2,0). 设所求线面角为α,则sin α=|cos〈n,〉|=.] 7.如图7721所示,二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为________. 图7721 60° [∵=++, ∴||= = ==2. ∴·=||·||·cos〈,〉=-24. ∴cos〈,〉=-. 又所求二面角与〈,〉互补, ∴所求的二面角为60°.] 8.在一直角坐标系中,已知A(-1,6),B(3,-8),现沿x轴将坐标平面折成60°的二面角,则折叠后A,B两点间的距离为________. 【导学号:79140256】 2 [如图为折叠后的图形,其中作AC⊥CD,BD⊥CD, 则AC=6,BD=8,CD=4, 两异面直线AC,BD夹角为60°. 故由=++, 得||2=|++|2=68, 所以||=2.] 三、解答题 9.(2018·合肥一检)如图7722,在四棱台ABCDA1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2. 图7722 (1)若M为CD的中点,求证:AM⊥平面AA1B1B; (2)求直线DD1与平面A1BD夹角的正弦值. [解] (1)证明:∵四边形ABCD为菱形,∠BAD=120°,连接AC,则△ACD为等边三角形, 又∵M为CD的中点,∴AM⊥CD, 由CD∥AB得AM⊥AB. ∵AA1⊥底面ABCD,AM底面ABCD, ∴AM⊥AA1,又∵AB∩AA1=A, ∴AM⊥平面AA1B1B. (2)∵四边形ABCD为菱形,∠BAD=120°, AB=AA1=2A1B1=2, 得DM=1,AM=,∴∠AMD=∠BAM=90°, 又∵AA1⊥底面ABCD, ∴以点A为原点,分别以AB,AM,AA1所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系Axyz, A1(0,0,2),B(2,0,0),D(-1,,0),D1, ∴1=,=(-3,,0), =(2,0,-2). 设平面A1BD的法向量为n=(x,y,z), 则有⇒ 令x=1,则n=(1,,1). ∴直线DD1与平面A1BD夹角θ的正弦值 sin θ=|cos〈n,1〉|==. 10.(2017·江苏高考)如图7723,在平行六面体ABCDA1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=,∠BAD=120°. 图7723 (1)求异面直线A1B与AC1夹角的余弦值; (2)求二面角BA1DA的正弦值. [解] 在平面ABCD内,过点A作AE⊥AD,交BC于点E. 因为AA1⊥平面ABCD,所以AA1⊥AE,AA1⊥AD. 如图,以{,,}为正交基底, 建立空间直角坐标系Axyz. 因为AB=AD=2,AA1=,∠BAD=120°, 则A(0,0,0),B(,-1,0),D(0,2,0),E(,0,0), A1(0,0,),C1(,1,). (1)=(,-1,-),=(,1,), 则cos〈,〉= ==-, 因此异面直线A1B与AC1夹角的余弦值为. (2)平面A1DA的一个法向量为=(,0,0). 设m=(x,y,z)为平面BA1D的一个法向量, 又=(,-1,-),=(-,3,0), 则即 不妨取x=3,则y=,z=2, 所以m=(3,,2)为平面BA1D的一个法向量. 从而cos〈,m〉===. 设二面角BA1DA的大小为θ,则|cos θ|=. 因为θ∈[0,π],所以sin θ==. 因此二面角BA1DA的正弦值为. B组 能力提升 11.(2017·河南百校联盟联考)已知斜四棱柱ABCDA1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD夹角的正切值为( ) 【导学号:79140257】 A. B. C. D. C [取AD中点O,连接OA1,易证A1O⊥平面ABCD.建立如图所示的空间直角坐标系, 得B(2,-1,0),D1(0,2,),=(-2,3,),平面ABCD的一个法向量为n=(0,0,1),设BD1与平面ABCD的夹角为θ,∴sin θ==, ∴tan θ=.] 12.已知点E,F分别在正方体ABCDA1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则平面AEF与平面ABC所成的二面角的正切值等于________. [延长FE,CB相交于点G,连接AG,如图所示. 设正方体的棱长为3,则GB=BC=3,作BH⊥AG于点H,连接EH,则∠EHB为所求二面角的平面角. ∵BH=,EB=1,∴tan∠EHB==.] 13.(2017·全国卷Ⅱ)如图7724,四棱锥PABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点. 图7724 (1)证明:直线CE∥平面PAB; (2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角MABD的余弦值. 【导学号:79140258】 [解] (1)证明:取PA的中点F,连接EF,BF. 因为E是PD的中点,所以EF∥AD,EF=AD. 由∠BAD=∠ABC=90°得BC∥AD, 又BC=AD,所以EFBC, 四边形BCEF是平行四边形,CE∥BF. 又BF平面PAB,CE平面PAB,故CE∥平面PAB. (2)由已知得BA⊥AD,以A为坐标原点,的方向为x轴正方向,||为单位长度,建立如图所示的空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,),=(1,0,-),=(1,0,0). 设M(x,y,z)(0查看更多
相关文章
- 当前文档收益归属上传用户