高二数学上学期周练7

高二数学上学期周练7

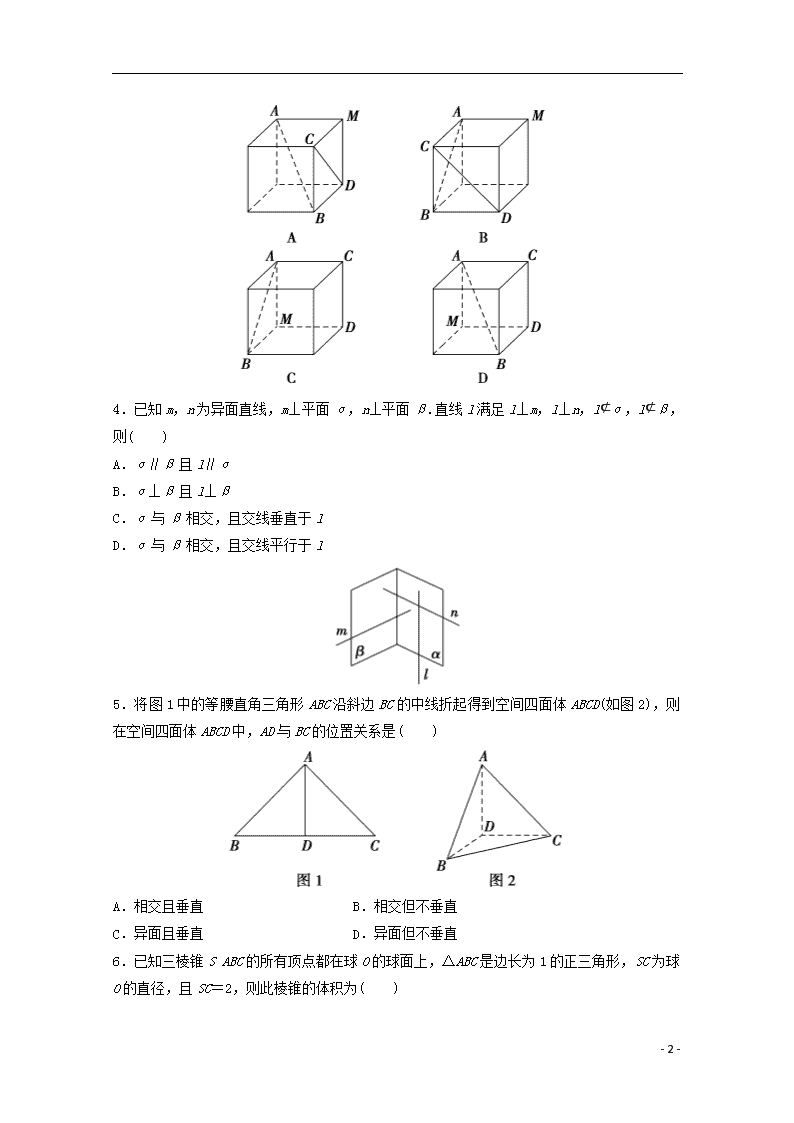
和诚中学2018-2019学年高二数学周练试题 时间：60分钟，满分：100分 ‎ 一、选择题：本题共6小题，每小题9分，在每小题给出的四个选项中，只有一项是 符合题目要求的．‎ ‎1．如图是一正方体被过棱的中点M、N和顶点A、D、C1的两个截面截去两个角后所得的几何体，则该几何体的主视图为(　　)‎ ‎2．如图所示，O为正方体ABCDA1B‎1C1D1的底面ABCD的中点，则下列直线中与B1O垂直的是(　　)‎ A．A1D B．AA1‎ C．A1D1 D．A‎1C1‎ ‎3．在如图所示的四个正方体中，能得出AB⊥CD的是(　　)‎ - 7 -‎ ‎4．已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(　　)‎ A．α∥β且l∥α B．α⊥β且l⊥β C．α与β相交，且交线垂直于l D．α与β相交，且交线平行于l ‎5．将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图2)，则在空间四面体ABCD中，AD与BC的位置关系是(　　)‎ A．相交且垂直 B．相交但不垂直 C．异面且垂直 D．异面但不垂直 ‎6．已知三棱锥SABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为(　　)‎ - 7 -‎ A. B. C. D. 二、填空题：本题共2小题，每小题9分．‎ ‎7．如图，在正方体ABCDA1B‎1C1D1中，点P是上底面A1B‎1C1D1内一动点，则三棱锥PABC的正视图与侧视图的面积的比值为________．‎ ‎8． 如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′＝6，O′C′＝2，则原图形OABC的面积为________．‎ 三、解答题： ‎ ‎9．(本小题满分14分) 10．如图，四棱锥PABCD中，底面ABCD是平行四边形，‎ 若Q是PC的中点，求证：PA∥平面BDQ；‎ ‎10．(本小题14分) 在如图所示的正方体中，分别棱是的中点，求异面直线与所成角的余弦值 - 7 -‎ 和诚中学2018-2019学年高二数学周练试题 ‎(时间：60分钟，满分：100分 命题人：)‎ 一、选择题：本题共6小题，每小题9分，在每小题给出的四个选项中，只有一项是 符合题目要求的．‎ ‎1．如图是一正方体被过棱的中点M、N和顶点A、D、C1的两个截面截去两个角后所得的几何体，则该几何体的主视图为(　　)‎ 解析：选B.还原正方体，如图所示，由题意可知，该几何体的主视图是选项B.‎ ‎2．如图所示，O为正方体ABCDA1B‎1C1D1的底面ABCD的中点，则下列直线中与B1O垂直的是(　　)‎ A．A1D B．AA1‎ C．A1D1 D．A‎1C1‎ 解析：选D.由题意知，A‎1C1⊥平面DD1B1B，又OB1⊂面DD1B1B，所以A‎1C1⊥OB1.‎ ‎3．在如图所示的四个正方体中，能得出AB⊥CD的是(　　)‎ - 7 -‎ 解析：选A.A选项中，∵CD⊥平面AMB，∴CD⊥AB，B选项中，AB与CD成60°角；C选项中，AB与CD成45°角；D选项中，AB与CD夹角的正切值为.‎ ‎4．已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(　　)‎ A．α∥β且l∥α B．α⊥β且l⊥β C．α与β相交，且交线垂直于l D．α与β相交，且交线平行于l 解析：选D.根据所给的已知条件作图，如图所示．‎ 由图可知α与β相交，且交线平行于l.‎ ‎5．将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图2)，则在空间四面体ABCD中，AD与BC的位置关系是(　　)‎ A．相交且垂直 B．相交但不垂直 - 7 -‎ C．异面且垂直 D．异面但不垂直 解析：选C.在题图1中的等腰直角三角形ABC中，斜边上的中线AD就是斜边上的高，则AD⊥BC，翻折后如题图2，AD与BC变成异面直线，而原线段BC变成两条线段BD、CD，这两条线段与AD垂直，即AD⊥BD，AD⊥CD，且BD∩CD＝D，故AD⊥平面BCD，所以AD⊥BC.‎ ‎6．已知三棱锥SABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为(　　)‎ A. B. C. D. 解析：选A.在直角三角形ASC中，AC＝1，∠SAC＝90°，SC＝2，所以SA＝＝；同理SB＝.过A点作SC的垂线交SC于D点，连接DB，因为△SAC≌△SBC，所以BD⊥SC，故SC⊥平面ABD，且平面ABD为等腰三角形，因为∠ASC＝30°，所以AD＝SA＝，则△ABD的面积为×1× ＝，则三棱锥的体积为××2＝.‎ 二、填空题：本题共2小题，每小题9分．‎ ‎7．如图，在正方体ABCDA1B‎1C1D1中，点P是上底面A1B‎1C1D1内一动点，则三棱锥PABC的正视图与侧视图的面积的比值为________．‎ 解析：如题图所示，设正方体的棱长为a，则三棱锥PABC的正(主)视图与侧(左)视图都是三角形，且面积都是a2，所以所求面积的比值为1.‎ 答案：1‎ ‎8． 如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′＝6，O′C′＝2，则原图形OABC的面积为________．‎ 解析：由题意知原图形OABC是平行四边形，且OA＝BC＝6，设平行四边形OABC的高为 OE，则OE××＝O′C′，‎ - 7 -‎ ‎∵O′C′＝2，∴OE＝4，∴S▱OABC＝6×4＝24.‎ 答案：24 三、解答题： ‎ ‎9．(本小题满分14分) 10．如图，四棱锥PABCD中，底面ABCD是平行四边形，‎ 若Q是PC的中点，求证：PA∥平面BDQ；‎ 解：证明：连接AC，交BD于点O，连接OQ.(图略)，‎ 因为O是AC的中点，‎ Q是PC的中点，所以OQ∥PA，‎ 又PA⊄平面BDQ，OQ⊂平面BDQ，所以PA∥平面BDQ.‎ ‎10．(本小题14分) 在如图所示的正方体中，分别棱是的中点，求异面直线与所成角的余弦值 ‎【答案】‎ ‎【解析】如下图，过E点作EM//AB,过M点作MN//AD,取MN中点G,所以面EMN//面ABCD，EG//BF, 异面直线与所成角,转化为，不妨设正方形边长为2，GE=,,在中，由余弦定理 - 7 -‎