2017-2018学年内蒙古北方重工业集团有限公司第三中学高二上学期期中考试数学（理）试题 Word版无答案

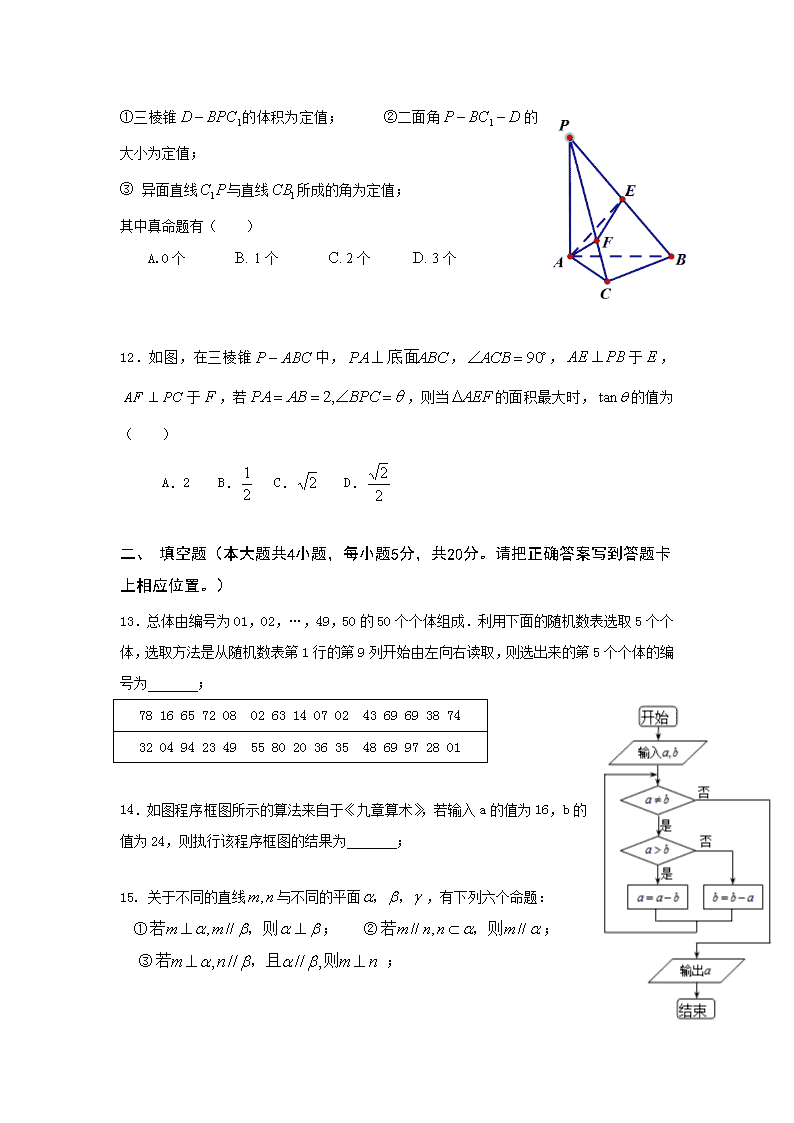
2017-2018学年内蒙古北方重工业集团有限公司第三中学高二上学期期中考试数学（理）试题 Word版无答案

北重三中2017～2018学年度第一学期 高二年级期中考试理科数学试题 一、 选择题（本大题共12小题，每小题5分，共60分。每个小题只有一个正确选项，请把正确选项用2B铅笔涂到答题卡上相应位置。）‎ ‎1．完成下列抽样调查，较为合理的抽样方法依次是（　）‎ ‎①从30件产品中抽取3件进行检查；‎ ‎②某校高中三个年级共有2460人，其中高一830人、高二820人、高三810人，为了了解学生对数学的建议，拟抽取一个容量为300的样本；‎ ‎③某剧场有28排，每排有32个座位，在一次报告中恰好坐满了听众，报告结束后，为了了解听众意见，需要请28名听众进行座谈．‎ A．①简单随机抽样，②系统抽样，③分层抽样 B．①分层抽样，②系统抽样，③简单随机抽样 C．①系统抽样，②简单随机抽样，③分层抽样 D．①简单随机抽样，②分层抽样，③系统抽样 ‎2．对满足的非空集合，有下列四个命题：‎ ‎①“若任取”是必然事件； ②“若”是不可能事件；‎ ‎③“若任取”是随机事件； ④“若”是必然事件．‎ 其中正确命题的个数为（　）‎ A． 4 B．3 C．2 D．1‎ ‎3. 用一个平面去截一个四棱锥，截面形状不可能的是（　）‎ ‎ A.三角形 B.四边形 C.五边形 D.六边形 ‎4．如图茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩（单位：分），已知甲组数据的众数为124，乙组数据的平均数为甲组数据的中位数，则的值分别为（　）‎ A．4，4 B．5，4 C．4，5 ‎ ‎ D．5，5‎ 5． 若同时掷两枚骰子，则向上的点数和是6的概率为(　）‎ ‎ A. B. C. D.‎ ‎6．某厂家为了解销售轿车台数与广告宣传费之间的关系，得到如表统计数据表：根据数据表可得回归直线方程，其中，据此模型预测广告费用为9万元时，销售轿车台数为（　）‎ 广告费用（万元）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6[]‎ 销售轿车（台数）[]‎ ‎3‎ ‎4‎ ‎6‎ ‎10‎ ‎12‎ A．17 B．18 C．19 D．20‎ ‎7．某几何体的三视图如图所示，俯视图是半径为2的圆，则该几何体的表面积为（　）‎ A． ‎ B． C． D． ‎ ‎8．已知P为空间中任意一点，四点满足任意三点均不共线，但四点共面，且，则实数的值为（　）‎ A． B． C． D．‎ ‎9．在三棱柱中，底面为棱长为1的正三角形，侧棱，点在棱上，且，若与平面所成的角为，则的值是（　）‎ A． B． C． D．‎ ‎10．如图所给的程序运行结果为，那么判断框中应填入的关于的条件是（　）‎ A． B． C． D．‎ ‎11. 在单位正方体中，点在线段上运动，给出以下四个命题： ‎ ‎①三棱锥的体积为定值； ②二面角的大小为定值； ‎ ‎③ 异面直线与直线所成的角为定值； 其中真命题有（　　）‎ A.0个 B. 1个 C. 2个 D. 3个 ‎[]‎ ‎12．如图，在三棱锥中，，，于，于，若，则当的面积最大时，的值为（　　）‎ A．2 B． C． D．‎ 二、 ‎ 填空题（本大题共4小题，每小题5分，共20分。请把正确答案写到答题卡上相应位置。）‎ ‎13．总体由编号为01，02，…，49，50的50个个体组成．利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第9列开始由左向右读取，则选出来的第5个个体的编号为　 　；‎ ‎78 16 65 72 08 02 63 14 07 02 43 69 69 38 74‎ ‎32 04 94 23 49 55 80 20 36 35 48 69 97 28 01‎ 14． 如图程序框图所示的算法来自于《九章算术》，若输入a的值为16，b的值为24，则执行该程序框图的结果为　 　；‎ ‎15. 关于不同的直线与不同的平面，有下列六个命题： ‎ ‎①； ②； ‎ ‎③ ； ‎ ‎④ ； ⑤；‎ ‎ ⑥； 其中正确命题的序号是________________________；‎ ‎16. 如图，在中，，，点为的中点，将沿折起到的位置，使，连接，得到三棱锥，若该三棱锥的所有顶点都在同一球面上，则该球的表面积是______________________。‎ 三、解答题（本大题共6小题，共70分。请将解答过程写到答题卡上相应位置。）‎ ‎17．（本小题满分10分）袋中装有除颜色外形状大小完全相同的6个小球，其中有4个编号为1，2，3，4的红球，2个编号为的黑球，现从中任取2个小球．‎ ‎（Ⅰ）求所取取2个小球都是红球的概率；‎ ‎（Ⅱ）求所取的2个小球颜色不相同的概率．‎ ‎18．（本小题满分12分）空气质量按照空气质量指数大小分为七档（五级），相对应空气质量的七个类别，指数越大，说明污染的情况越严重，对人体危害越大．‎ 指数 级别 类别 户外活动建议 ‎[0,50)‎ Ⅰ 优 可正常活动 ‎[50,100)‎ Ⅱ 良 ‎[100,150)‎ Ⅲ 轻微污染 易感人群症状有轻度加剧，健康人群出现刺激症状，心脏病和呼吸系统疾病患者应减少体积消耗和户外活动．‎ ‎[150,200)‎ 轻度污染 ‎[200,250)‎ Ⅳ 中度污染 心脏病和肺病患者症状显著加剧，运动耐受力降低，健康人群中普遍出现症状，老年人和心脏病、肺病患者应减少体力活动．‎ ‎[250,300)‎ 中度重污染 ‎[300,500]‎ Ⅴ 重污染 健康人运动耐受力降低，由明显强烈症状，提前出现某些疾病，老年人和病人应当留在室内，避免体力消耗，一般人群应尽量减少户外活动．‎ 现统计包头市市区2016年10月至11月连续60天的空气质量指数，制成如图所示的频率分布直方图．‎ ‎（Ⅰ）求这60天中属轻度污染的天数；‎ ‎（Ⅱ）将频率分布直方图中的五组从左到右依次命名为第一组，第二组，…，第五组．从第一组和第五组中的所有天数中抽出两天，记它们的空气质量指数分别为，求事件的概率．‎ ‎19. （本小题满分12分）设函数 ‎（Ⅰ）若，求函数有零点的概率；‎ ‎（Ⅱ）若，求函数无零点的概率．‎ 20. ‎（本小题满分12分）如图，梯形中，‎ ‎，沿对角线将折起，使点在平面内的射影恰在上． (Ⅰ)求证：； (Ⅱ)求异面直线与所成的角； (Ⅲ)求二面角的余弦值． ‎ ‎21．（本小题满分12分）某测试团队为了研究“饮酒”对“驾车安全”的影响，随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试．测试的方案：电脑模拟驾驶，以某速度匀速行驶，记录下驾驶员的“停车距离”（驾驶员从看到意外情况到车子完全停下所需要的距离）．无酒状态与酒后状态下的试验数据分别列于表1和表2．‎ 表1‎ 停车距离（米）‎ ‎（10，20]‎ ‎（20，30][]‎ ‎（30，40]‎ ‎（40，50]‎ ‎（50，60]‎ 频数 ‎26‎ ‎8‎ ‎2‎ 表2‎ 平均每毫升血液酒精含量毫克 ‎10‎ ‎30‎ ‎50‎ ‎70‎ ‎90‎ 平均停车距离米 ‎30‎ ‎50‎ ‎60‎ ‎70‎ ‎90‎ 已知表1数据的中位数估计值为26，回答以下问题．‎ ‎（Ⅰ）求的值，并估计驾驶员无酒状态下停车距离的平均数；‎ ‎（Ⅱ）根据最小二乘法，由表2的数据计算关于的回归方程；‎ ‎（Ⅲ）该测试团队认为：驾驶员酒后驾车的平均“停车距离”大于（Ⅰ）中无酒状态下的停车距离平均数的3倍，则认定驾驶员是“醉驾”．请根据（Ⅱ）中的回归方程，预测当每毫升血液酒精含量大于多少毫克时为“醉驾”？‎ ‎（附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为）‎ ‎22．（本小题满分12分）某设计部门承接一产品包装盒的设计（如图所示），客户除了要求边的长分别为20和30外，还特别要求包装盒必需满足：①平面平面；②平面与平面所成的二面角不小于；③包装盒的体积尽可能大．若设计部门设计出的样品满足：与均为直角且长20，矩形的一边长为30，请你判断该包装盒的设计是否能符合客户的要求？说明理由．‎ ‎　‎