- 2021-06-16 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习北师大版概率、随机变量及其分布列教案
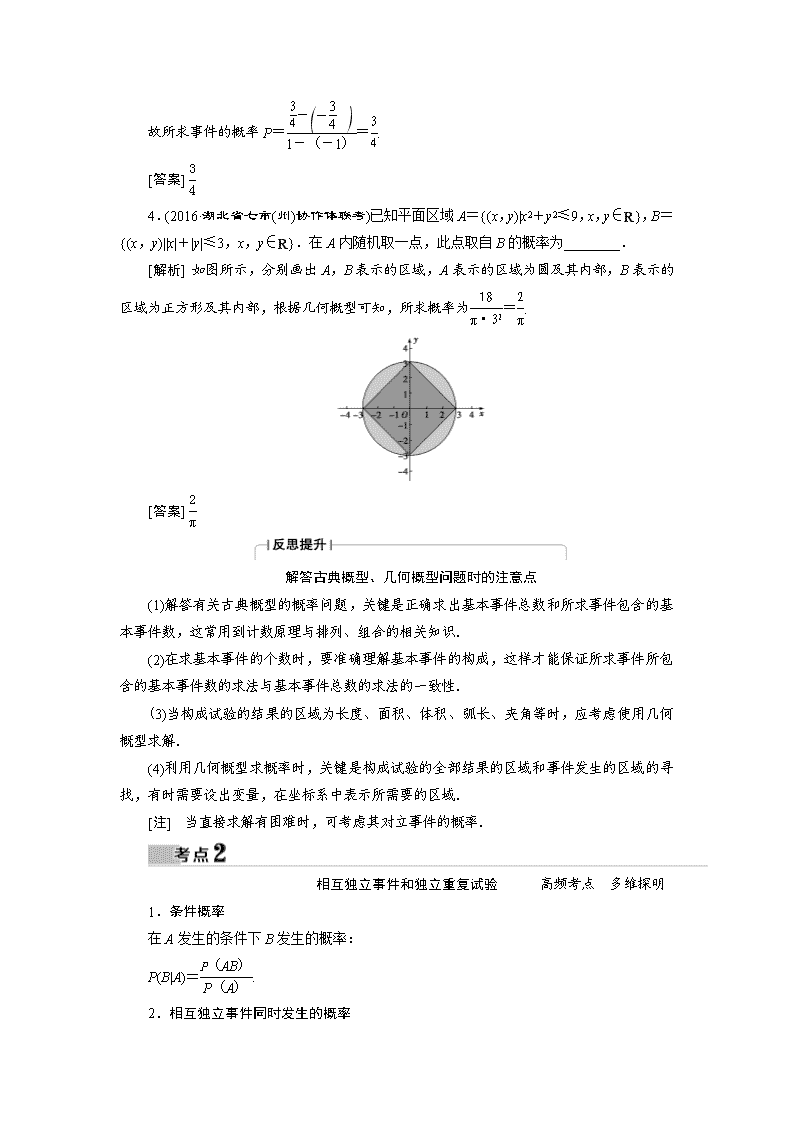
第2讲 概率、随机变量及其分布列 古典概型与几何概型 自主练透 夯实双基 1.古典概型的概率 P(A)==. 2.几何概型的概率 P(A)=. [题组通关] 1.(2016·高考全国卷丙)小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是( ) A. B. C. D. C [解析] 开机密码的所有可能结果有:(M,1),(M,2),(M,3),(M,4),(M,5),(I,1),(I,2),(I,3),(I,4),(I,5),(N,1),(N,2),(N,3),(N,4),(N,5),共15种,所以小敏输入一次密码能够成功开机的概率是,故选C. 2.袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( ) A. B. C. D.1 B [解析] 从15个球中任取2个球共有C种取法,其中有1个红球,1个白球的情况有C·C=50(种),所以P==. 3.(2016·高考山东卷)在[-1,1]上随机地取一个数k,则事件“直线y=kx与圆(x-5)2+y2=9相交”发生的概率为________. [解析] 圆(x-5)2+y2=9的圆心为C(5,0),半径r=3,故由直线与圆相交可得<r,即<3,整理得k2<,得-<k<. 故所求事件的概率P==. [答案] 4.(2016·湖北省七市(州)协作体联考)已知平面区域A={(x,y)|x2+y2≤9,x,y∈R},B={(x,y)||x|+|y|≤3,x,y∈R}.在A内随机取一点,此点取自B的概率为________. [解析] 如图所示,分别画出A,B表示的区域,A表示的区域为圆及其内部,B表示的区域为正方形及其内部,根据几何概型可知,所求概率为=. [答案] 解答古典概型、几何概型问题时的注意点 (1)解答有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数,这常用到计数原理与排列、组合的相关知识. (2)在求基本事件的个数时,要准确理解基本事件的构成,这样才能保证所求事件所包含的基本事件数的求法与基本事件总数的求法的一致性. (3)当构成试验的结果的区域为长度、面积、体积、弧长、夹角等时,应考虑使用几何概型求解. (4)利用几何概型求概率时,关键是构成试验的全部结果的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域. [注] 当直接求解有困难时,可考虑其对立事件的概率. 相互独立事件和独立重复试验 高频考点 多维探明 1.条件概率 在A发生的条件下B发生的概率: P(B|A)=. 2.相互独立事件同时发生的概率 P(AB)=P(A)P(B). 3.独立重复试验、二项分布 如果事件A在一次试验中发生的概率是p,那么它在n次独立重复试验中恰好发生k次的概率为: Pn(k)=Cpk(1-p)n-k,k=0,1,2,…,n. 条件概率 (2016·高考全国卷甲节选)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下: 上年度出险次数 0 1 2 3 4 ≥5 保费 0.85a a 1.25a 1.5a 1.75a 2a 设该险种一续保人一年内出险次数与相应概率如下: 一年内出险次数 0 1 2 3 4 ≥5 概率 0.30 0.15 0.20 0.20 0.10 0.05 (1)求一续保人本年度的保费高于基本保费的概率; (2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率. 【解】 (1)设A表示事件:“一续保人本年度的保费高于基本保费”,则事件A发生当且仅当一年内出险次数大于1,故P(A)=0.20+0.20+0.10+0.05=0.55. (2)设B表示事件:“一续保人本年度的保费比基本保费高出60%”,则事件B发生当且仅当一年内出险次数大于3,故P(B)=0.10+0.05=0.15. 又P(AB)=P(B),故 P(B|A)====. 因此所求概率为. 相互独立事件的概率 (2016·开封市第一次模拟)某生物产品,每一个生产周期成本为20万元,此产品的产量受气候影响、价格受市场影响均具有随机性,且互不影响,其具体情况如下表: 产量(吨) 30 50 概率 0.5 0.5 市场价格(万元/吨) 0.6 1 概率 0.4 0.6 (1)设X表示1个生产周期此产品的利润,求X的分布列; (2)连续3个生产周期,求这3个生产周期中至少有2个生产周期的利润不少于10万元的概率. 【解】 (1)设A表示事件“产品产量为30吨”,B表示事件“产品市场价格为0.6万元/吨”,则P(A)=0.5,P(B)=0.4, 因为利润=产量×市场价格-成本, 所以X的所有值为 50×1-20=30,50×0.6-20=10, 30×1-20=10,30×0.6-20=-2, 则P(X=30)=P(A)P(B)=(1-0.5)×(1-0.4)=0.3, P(X=10)=P(A)P(B)+P(A)P(B)=(1-0.5)×0.4+0.5×(1-0.4)=0.5, P(X=-2)=P(A)P(B)=0.5×0.4=0.2, 则X的分布列为 X 30 10 -2 P 0.3 0.5 0.2 (2)设Ci表示事件“第i个生产周期的利润不少于10万元”(i=1,2,3), 则C1,C2,C3相互独立, 由(1)知,P(Ci)=P(X=30)+P(X=10)=0.3+0.5=0.8(i=1,2,3), 连续3个生产周期的利润均不少于10万元的概率为P(C1C2C3)=P(C1)P(C2)P(C3)=0.83=0.512, 连续3个生产周期中有2个生产周期的利润不少于10万元的概率为P(C1C2C3)+P(C1C2C3)+P(C1C2C3)=3×0.82×0.2=0.384, 所以连续3个生产周期中至少有2个生产周期的利润不少于10万元的概率为0.512+0.384=0.896. 独立重复试验的概率 在全国大学生智能汽车总决赛中,某高校学生开发的智能汽车在一个标注了平面直角坐标系的平面上从坐标原点出发,每次只能移动一个单位,沿x轴正方向移动的概率是,沿y轴正方向移动的概率为,则该智能汽车移动6次恰好移动到点(3,3)的概率为________. 【解析】 若该机器人移动6次恰好到点(3,3),则机器人在移动过程中沿x轴正方向移动3次,沿y轴正方向移动3次, 所以机器人移动6次恰好位于点(3,3)的概率: P=C=20×=. 【答案】 求相互独立事件和独立重复试验的概率的注意点 (1)求复杂事件的概率,要正确分析复杂事件的构成,看复杂事件能转化为几个彼此互斥的事件的和事件还是能转化为几个相互独立事件同时发生的积事件,然后用概率公式求解. (2)一个复杂事件若正面情况比较多,反面情况较少,则一般利用对立事件进行求解.对于“至少”“至多”等问题往往用这种方法求解. (3)注意辨别独立重复试验的基本特征:①在每次试验中,试验结果只有发生与不发生两种情况;②在每次试验中,事件发生的概率相同. (4)牢记公式Pn(k)=Cpk(1-p)n-k,k=0,1,2,…,n,并深刻理解其含义. [注] 注意区分互斥事件和相互独立事件,互斥事件是在同一试验中不可能同时发生的两个事件,相互独立事件是指几个事件的发生与否互不影响,当然可以同时发生. [跟踪训练] 在某中学举办的校园文化周活动中,从周一到周五的五天中,每天安排一项内容不同的活动供学生选择参加,要求每位学生必须参加三项活动,其中甲同学必须参加周一的活动,不参加周五的活动,其余三天的活动随机选择两项参加,乙同学和丙同学可以在周一到周五中随机选择三项参加. (1)求甲同学选周三的活动且乙同学未选周三的活动的概率; (2)设X表示甲、乙、丙三名同学选择周三的活动的人数之和,求X的分布列. [解] (1)设A表示事件“甲同学选周三的活动”,B表示事件“乙同学选周三的活动”,则P(A)==,P(B)==.因为事件A,B相互独立, 所以甲同学选周三的活动且乙同学未选周三的活动的概率为P(AB)=P(A)P(B)=×=. (2)设C表示事件“丙同学选周三的活动”,则 P(C)==.X的可能取值为0,1,2,3. P(X=0)=P(A·B·C)=××=, P(X=1)=P(ABC)+P(ABC)+P(ABC)=××+××+××=, P(X=2)=P(ABC)+P(ABC)+P(ABC)=××+××+××=, P(X=3)=P(ABC)=××=. 所以X的分布列为 X 0 1 2 3 P 随机变量的分布列、均值与方差 共研典例 类题通法 1.均值与方差的性质 (1)E(aX+b)=aE(X)+b; (2)D(aX+b)=a2D(X)(a,b为实数). 2.两点分布与二项分布的均值、方差 (1)若X服从两点分布,则E(X)=p,D(X)=p(1-p); (2)若X~B(n,p),则E(X)=np,D(X)=np(1-p). (2016·海口市调研测试)汽车租赁公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表: A型车 出租天数 1 2 3 4 5 6 7 车辆数 5 10 30 35 15 3 2 B型车 出租天数 1 2 3 4 5 6 7 车辆数 14 20 20 16 15 10 5 (1)从出租天数为3的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率; (2)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4的概率; (3)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,建议应该购买哪一种车型,并说明你的理由. 【解】 (1)估计这辆汽车是A型车的概率P==0.60. (2)设“事件Ai表示一辆A型车在一周内出租天数恰好为i”, “事件Bj表示一辆B型车在一周内出租天数恰好为j”,其中i,j=1,2,3,…,7, 则该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4的概率为P(A1B3+ A2B2+A3B1)=P(A1B3)+P(A2B2)+P(A3B1)=P(A1)P(B3)+P(A2)P(B2)+P(A3)P(B1)=×+×+×=, 故该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4的概率为. (3)设X为A型车出租的天数,则X的分布列为 X 1 2 3 4 5 6 7 P 0.05 0.10 0.30 0.35 0.15 0.03 0.02 设Y为B型车出租的天数,则Y的分布列为 Y 1 2 3 4 5 6 7 P 0.14 0.20 0.20 0.16 0.15 0.10 0.05 E(X)=1×0.05+2×0.10+3×0.30+4×0.35+5×0.15+6×0.03+7×0.02=3.62, E(Y)=1×0.14+2×0.20+3×0.20+4×0.16+5×0.15+6×0.10+7×0.05=3.48. 一辆A型车一个星期出租天数的平均值为3.62,B型车一个星期出租天数的平均值为3.48,选择A型车更加合理. 求解随机变量分布列问题的两个关键点 (1)求离散型随机变量分布列的关键是正确理解随机变量取每一个值所表示的具体事件,然后综合应用各类概率公式求概率. (2)求随机变量均值与方差的关键是正确求出随机变量的分布列.若随机变量服从二项分布,则可直接使用公式法求解. [跟踪训练] 某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A区投篮2次或选择在B区投篮3次,在A区每进一球得2分,不进球得0分;在B区每进一球得3分,不进球得0分,得分高的选手胜出.已知某参赛选手甲在A区和B区每次投篮进球的概率分别是和. (1)如果该选手以在A,B区投篮得分的期望高者为选择投篮区的标准,问该选手应该选择哪个区投篮?请说明理由; (2)求该选手在A区投篮得分高于在B区投篮得分的概率. [解] (1)设选手甲在A区投篮的得分为ξ,则ξ的可能取值为0,2,4. P(ξ=0)==, P(ξ=2)=C·==, P(ξ=4)==, 所以ξ的分布列为 ξ 0 2 4 P 所以E(ξ)=3.6. 同理,设选手甲在B区投篮的得分为η,则η的可能取值为0,3,6,9. P(η=0)==, P(η=3)=C·=, P(η=6)=C=, P(η=9)==, 所以η的分布列为 η 0 3 6 9 P 所以E(η)=3,因为E(ξ)>E(η),所以选手甲应该选择A区投篮. (2)设选手甲在A区投篮得分高于在B区投篮得分为事件C,由(1)知: P(C)=P(ξ>η)=P(ξ=4且η=3或0)+P(ξ=2且η=0)=×+×=, 故选手甲在A区投篮得分高于B区投篮得分的概率为. 课时作业 1.国庆节放假,甲去北京旅游的概率为,乙、丙去北京旅游的概率分别为、.假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( ) A. B. C. D. B [解析] 因为甲、乙、丙去北京旅游的概率分别为、、.所以他们不去北京旅游的概率分别为、、,所以至少有1人去北京旅游的概率P=1-××=. 2.(2016·贵阳市监测考试)在[-4,4]上随机取一个实数m,能使函数f(x)=x3+mx2+3x 在R上单调递增的概率为( ) A. B. C. D. D [解析] 由题意,得f′(x)=3x2+2mx+3,要使函数f(x)在R上单调递增,则3x2+2mx+3≥0在R上恒成立,即Δ=4m2-36≤0,解得-3≤m≤3,所以所求概率为=,故选D. 3.某盒中装有10只乒乓球,其中6只新球,4只旧球,不放回地依次摸出2个球使用,在第一次摸出新球的条件下,第二次也摸到新球的概率为( ) A. B. C. D. B [解析] 第一次摸出新球记为事件A,则P(A)=,第二次摸到新球记为事件B,则P(AB)==,所以P(B|A)===,故选B. 4.两人掷一枚硬币,掷出正面多者为胜,但这枚硬币质地不均匀,以致出现正面的概率P1与出现反面的概率P2不相等.已知出现正面与出现反面是对立事件,设两人各掷一次成平局的概率为P,则P与0.5的大小关系是( ) A.P<0.5 B.P=0.5 C.P>0.5 D.不确定 C [解析] 据题意知两人掷一次成平局这一事件包含:两人均出现正面,两人均出现反面.故其概率为P=P+P=(P1+P2)2-2P1P2=1-2P1P2>1-2=.(注意条件中出现正面和出现反面是对立事件,故P1+P2=1.又P1≠P2,故由基本不等式得上式) 5.已知P是△ABC所在平面内一点,++2=0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( ) A. B. C. D. D [解析] 以PB、PC为邻边作平行四边形PBDC,则+=,因为++2=0,所以 +=-2,得=-2,由此可得, P是△ABC边BC上的中线AO的中点,点P到BC的距离等于A到BC距离的,所以S△PBC=S△ABC,所以将一粒黄豆随机撒在△ABC内,黄豆落在△PBC内的概率为=,故选D. 6.(2016·高考全国卷甲)从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为( ) A. B. C. D. C [解析] 设由构成的正方形的面积为S,x+y<1构成的图形的面积为S′,所以==,所以π=,故选C. 7.已知集合M={1,2,3,4},N={(a,b)|a∈M,b∈M},A是集合N中任意一点,O为坐标原点,则直线OA与抛物线y=x2+1有交点的概率是________. [解析] 易知过点(0,0)与抛物线y=x2+1相切的直线为y=2x(斜率小于0的无需考虑),集合N中共有16个元素,其中使OA斜率不小于2的有(1,2),(1,3),(1,4),(2,4),共4个,由古典概型的概率计算公式知概率为P==. [答案] 8.某商场在儿童节举行回馈顾客活动,凡在商场消费满100元者即可参加射击赢玩具活动,具体规则如下:每人最多可射击3次,一旦击中,则可获奖且不再继续射击,否则一直射击到3次为止.设甲每次击中的概率为p(p≠0),射击次数为η,若η的数学期望E(η)>,则p的取值范围是________. [解析] 由已知得P(η=1)=p,P(η=2)=(1-p)p,P(η=3)=(1-p)2,则E(η)=p+2(1-p)p+3(1-p)2=p2-3p+3>,解得p>或p<,又p∈(0,1),所以p∈. [答案] 9.如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为圆心,1为半径在三角形内作圆弧,三段圆弧与斜边围成区域M(图中白色部分).若在此三角形内随机取一点P,则点P落在区域M 内的概率为________. [解析] S阴影=2××π×12+×π×12=, 所以点P落在区域M内的概率为==1-. [答案] 1- 10.如图,在长方体ABCDA1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCDA1B1C1D1内随机选取一点,则该点取自于几何体A1ABFED1DCGH内的概率为________. [解析] 因为EH∥A1D1,所以EH∥B1C1,所以EH∥平面BCC1B1.过EH的平面与平面BCC1B1交于FG,则EH∥FG,所以易证明几何体A1ABFED1DCGH和EB1FHC1G分别是等高的五棱柱和三棱柱,由几何概型可知,所求概率为:P=1-=1-=1-=. [答案] 11.(2016·高考天津卷)某小组共10人,利用假期参加义工活动.已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中随机选出2人作为该组代表参加座谈会. (1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率; (2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望. [解] (1)由已知,有P(A)==. 所以,事件A发生的概率为. (2)随机变量X的所有可能取值为0,1,2. P(X=0)==, P(X=1)==, P(X=2)==. 所以,随机变量X的分布列为 X 0 1 2 P 随机变量X的数学期望E(X)=0×+1×+2×=1. 12.(2016·河南省六市第一次联考)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表: 降水量X X<300 300≤X<700 700≤X<900 X≥900 工期延 误天数Y 0 2 6 10 历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,求: (1)工期延误天数Y的均值与方差; (2)在降水量X至少是300的条件下,工期延误不超过6天的概率. [解] (1)由已知条件和概率的加法公式,有 P(X<300)=0.3, P(300≤X<700)=0.7-0.3=0.4, P(700≤X<900)=0.9-0.7=0.2, P(X≥900)=1-P(X<900)=1-0.9=0.1. 所以Y的分布列为 Y 0 2 6 10 P 0.3 0.4 0.2 0.1 所以E(Y)=0×0.3+2×0.4+6×0.2+10×0.1=3; D(Y)=(0-3)2×0.3+(2-3)2×0.4+(6-3)2×0.2+(10-3)2×0.1=9.8. 故工期延误天数Y的均值为3,方差为9.8. (2)由题可得,P(X≥300)=1-P(X<300)=0.7, 又P(300≤X<900)=0.9-0.3=0.6. 由条件概率,得 P(Y≤6|X≥300)=P(X<900|X≥300)===. 故在降水量至少是300的条件下,工期延误不超过6天的概率是. 13.(2016·沈阳市教学质量监测(一))某中学根据2002~2014年期间学生的兴趣爱好, 分别创建了“摄影”“棋类”“国学”三个社团,据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2015年某新生入学,假设他通过考核选拔进入该校的“摄影”“棋类”“国学”三个社团的概率依次为m、、n,已知三个社团他都能进入的概率为,至少进入一个社团的概率为,且m>n. (1)求m与n的值; (2)该校根据三个社团活动安排情况,对进入“摄影”社的同学增加校本选修学分1分,对进入“棋类”社的同学增加校本选修学分2分,对进入“国学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课学分分数的分布列及期望. [解] (1)依题可知,,解得. (2)令该新同学在社团方面获得校本选修课学分的分数为随机变量X,则X的值可以为0,1,2,3,4,5,6. 而P(X=0)=××=;P(X=1)=××=;P(X=2)=××=;P(X=3)=××+××=; P(X=4)=××=;P(X=5)=××=; P(X=6)=××=. X的分布列为 X 0 1 2 3 4 5 6 P 于是,E(X)=0×+1×+2×+3×+4×+5×+6×=. 14.(2016·广州市高考模拟)计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立. (1)求在未来4年中,至多1年的年入流量超过120的概率; (2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系: 年入流量X 40查看更多