【数学】2019届文科一轮复习人教A版2-5指数函数教案

【数学】2019届文科一轮复习人教A版2-5指数函数教案

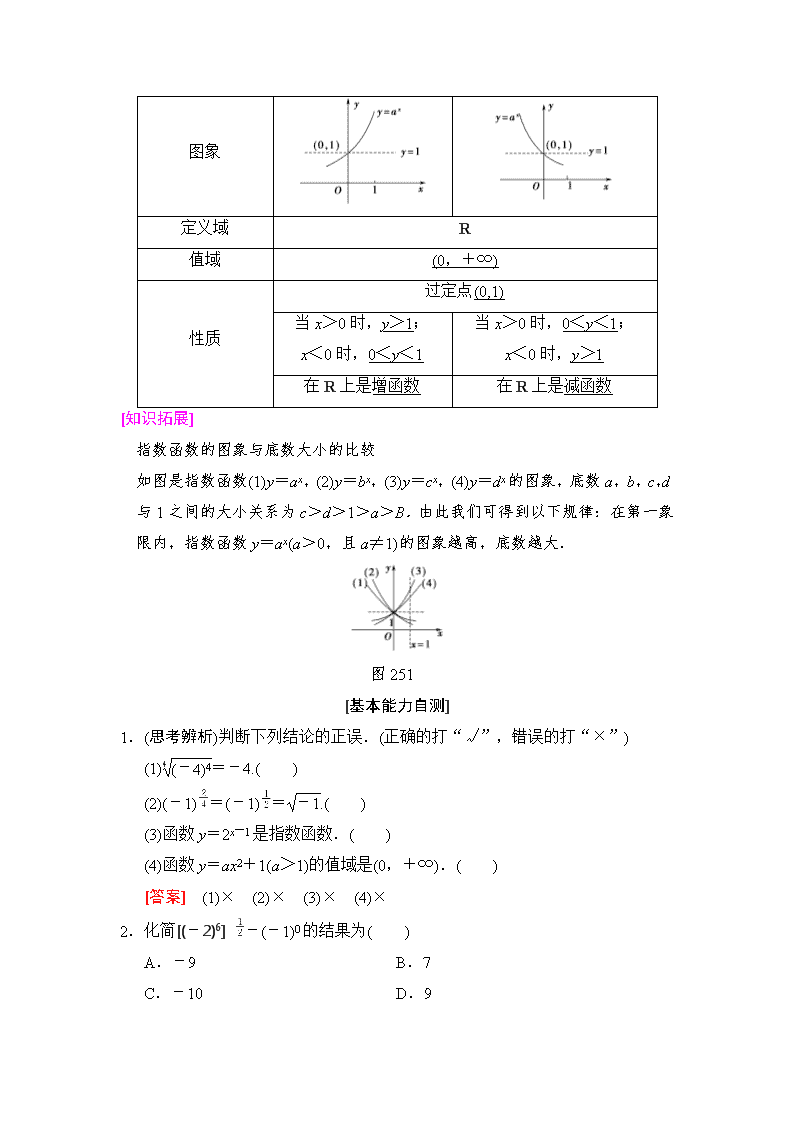
第五节　指数函数 ‎ [考纲传真]　(教师用书独具)1.理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算.2.了解指数函数模型的实际背景，理解指数函数的概念及其单调性，掌握指数函数图象通过的特殊点，会画底数为2,3,10，，的指数函数的图象.3.体会指数函数是一类重要的函数模型．‎ ‎(对应学生用书第16页)‎ ‎ [基础知识填充]‎ ‎1．根式的性质 ‎ (1)()n＝a．‎ ‎ (2)当n为奇数时，＝a．‎ ‎ (3)当n为偶数时，＝|a|＝ ‎ (4)负数的偶次方根无意义．‎ ‎ (5)零的任何次方根都等于零．‎ ‎2．有理数指数幂 ‎ (1)分数指数幂 ‎ ①正分数指数幂：a＝(a＞0，m，n∈N*，且n＞1)；‎ ‎ ②负分数指数幂：a＝＝(a＞0，m，n∈N*，且n＞1)；‎ ‎ ③0的正分数指数幂等于0,0的负分数指数幂没有意义．‎ ‎ (2)有理数指数幂的运算性质 ‎ ①ar·as＝ar＋s(a＞0，r，s∈Q)；‎ ‎ ②(ar)s＝ars(a＞0，r，s∈Q)；‎ ‎ ③(ab)r＝arbr(a＞0，b＞0，r∈Q)．‎ ‎3．指数函数的图象与性质 y＝ax a＞1‎ ‎0＜a＜1‎ 图象 定义域 R 值域 ‎(0，＋∞)‎ 性质 过定点(0,1)‎ 当x＞0时，y＞1；‎ x＜0时，0＜y＜1‎ 当x＞0时，0＜y＜1；‎ x＜0时，y＞1‎ 在R上是增函数 在R上是减函数 ‎[知识拓展]‎ ‎　指数函数的图象与底数大小的比较 ‎ 如图是指数函数(1)y＝ax，(2)y＝bx，(3)y＝cx，(4)y＝dx的图象，底数a，b，c，d与1之间的大小关系为c＞d＞1＞a＞B．由此我们可得到以下规律：在第一象限内，指数函数y＝ax(a＞0，且a≠1)的图象越高，底数越大．‎ 图251‎ ‎[基本能力自测]‎ ‎1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎ (1)＝－4.(　　)‎ ‎ (2)(－1)＝(－1)＝.(　　)‎ ‎ (3)函数y＝2x－1是指数函数．(　　)‎ ‎ (4)函数y＝ax2＋1(a＞1)的值域是(0，＋∞)．(　　)‎ ‎ [答案]　(1)×　(2)×　(3)×　(4)×‎ ‎2．化简[(－2)6] －(－1)0的结果为(　　)‎ ‎ A．－9　　　　 B．7　　　　‎ ‎ C．－10　　　　 D．9‎ ‎ B　[原式＝(26)－1＝8－1＝7.]　‎ ‎3．(教材改编)若函数f(x)＝ax(a＞0，且a≠1)的图象经过点P，则f(－1)等于(　　)‎ ‎ A． B． ‎ ‎ C． D．4‎ ‎ B　[由题意知＝a2，所以a＝，‎ ‎ 所以f(x)＝x，所以f(－1)＝－1＝.]‎ ‎4．函数y＝ax－a(a＞0，且a≠1)的图象可能是(　　)‎ ‎ A　　 　　B　　 　 C　 　 　　D ‎ C　[法一：令y＝ax－a＝0，得x＝1，即函数图象必过定点(1,0)，符合条件的只有选项C．‎ ‎ 法二：当a＞1时，y＝ax－a是由y＝ax向下平移a个单位，且过(1,0)，A，B，D都不合适；‎ ‎ 当0＜a＜1时，y＝ax－a是由y＝ax向下平移a个单位，因为0＜a＜1，故排除选项D．]‎ ‎5．指数函数y＝(2－a)x在定义域内是减函数，则a的取值范围是________．‎ ‎ (1,2)　[由题意知0＜2－a＜1，解得1＜a＜2.]‎ ‎(对应学生用书第17页)‎ 指数幂的运算 ‎　化简求值：‎ ‎ (1)0＋2－2· －(0.01)0.5；‎ ‎ ‎ ‎ [解]　(1)原式＝1＋×－＝1＋×－＝1＋－＝.‎ ‎ (2)原式＝.‎ ‎ [规律方法]　　1.指数幂的运算，首先将根式、分数指数幂统一为分数指数幂，以便利用法则计算，但应注意：‎ ‎ (1)必须同底数幂相乘，指数才能相加；‎ ‎ (2)运算的先后顺序．‎ ‎ 2．当底数是负数时，先确定符号，再把底数化为正数．‎ ‎ 3．运算结果不能同时含有根号和分数指数，也不能既有分母又含有负指数．‎ ‎[变式训练1]　化简求值：‎ ‎ (1)(0.027)－－2＋－(－1)0；‎ ‎ ‎ ‎ [解]　(1)原式＝－72＋－1‎ ‎ ＝－49＋－1＝－45.‎ ‎ ‎ ‎ ＝－·＝－.‎ 指数函数的图象及应用 ‎　(1)(2018·益阳模拟)函数y＝e－|x－1|图象的大致形状是(　　)‎ ‎ (2)若曲线y＝|2x－1|与直线y＝b有两个公共点，求b的取值范围. ‎ ‎【导学号：79170029】‎ ‎ (1)B　[y＝e－|x－1|＝|x－1|，因此原函数的图象是函数y＝|x|的图象向右平移一个单位得到的，故选B．]‎ ‎ (2)曲线y＝|2x－1|与直线y＝b的图象如图所示，由图象可得，如果曲线y＝|2x－1|与直线y＝b有两个公共点，‎ ‎ 则b的取值范围是(0,1)．‎ ‎ [规律方法]　　指数函数图象的画法(判断)及应用 ‎ (1)画(判断)指数函数y＝ax(a＞0，a≠1)的图象，应抓住三个关键点：(1，a)，(0,1)，.‎ ‎ (2)与指数函数有关的函数的图象的研究，往往利用相应指数函数的图象，通过平移、对称变换得到其图象．‎ ‎ (3)一些指数方程、不等式问题的求解，往往利用相应的指数型函数图象数形结合求解. ‎ ‎ [变式训练2]　(1)函数f(x)＝ax－b的图象如图252，其中a，b为常数，则下列结论正确的是(　　)‎ 图252‎ ‎ A．a＞1，b＜0‎ ‎ B．a＞1，b＞0‎ ‎ C．0＜a＜1，b＞0‎ ‎ D．0＜a＜1，b＜0‎ ‎ (2)方程 2x＝2－x的解的个数是________．‎ ‎ (1)D　(2)1　[(1)由f(x)＝ax－b的图象可以观察出，函数f(x)＝ax－b在定义域上单调递减，所以0＜a＜1，函数f(x)＝ax－b的图象是在y＝ax的基础上向左平移得到的，所以b＜0.‎ ‎ (2)方程的解可看作函数y＝2x和y＝2－x的图象交点的横坐标，分别作出这两个函数图象(如图)．‎ ‎ 由图象得只有一个交点，因此该方程只有一个解．]‎ 指数函数的性质及应用 角度1　比较大小或解不等式 ‎　(1)(2018·贵阳模拟)已知a＝2，b＝4，c＝25，则(　　)‎ ‎ A．b＜a＜c　　　　　 B．a＜b＜c ‎ C．b＜c＜a D．c＜a＜b ‎ (2)(2018·兰州模拟)不等式2x2－x＜4的解集为________．‎ ‎ (1)A　(2){x|－1＜x＜2}　[(1)因为a＝2＝16，b＝4＝16，c＝25，且幂函数y＝x在R上单调递增，指数函数y＝16x在R上单调递增，所以b＜a＜C．‎ ‎ (2)由2x2－x＜4得2x2－x＜22.‎ ‎ 所以x2－x＜2，解得－1＜x＜2.]‎ 角度2　复合函数的单调性、值域或最值 ‎　已知函数f(x)＝ax2－4x＋3.‎ ‎ (1)若a＝－1，求f(x)的单调区间；‎ ‎ (2)若f(x)有最大值3，求a的值；‎ ‎ (3)若f(x)的值域是(0，＋∞)，求a的值．‎ ‎【导学号：79170030】‎ ‎ [解]　(1)当a＝－1时，f(x)＝－x2－4x＋3，‎ ‎ 令g(x)＝－x2－4x＋3＝－(x＋2)2＋7，‎ ‎ 则g(x)在区间(－∞，－2)上单调递增，‎ ‎ 在区间[－2，＋∞)上单调递减，又函数y＝x在R上是减函数，‎ ‎ 因此f(x)的单调递增区间是[－2，＋∞)，单调递减区间是(－∞，－2)．‎ ‎ (2)由f(x)有最大值3知，ax2－4x＋3有最小值－1，则有解得a＝1.‎ ‎ (3)由f(x)的值域是(0，＋∞)知，ax2－4x＋3的值域为R，则必有a＝0.‎ ‎ [规律方法]　　1.比较指数式的大小的方法是：(1)能化成同底数的先化成同底数幂，再利用单调性比较大小；(2)不能化成同底数的，一般引入“‎1”‎等中间量比较大小．‎ ‎ 2．解简单的指数方程或不等式可先利用幂的运算性质化为同底数幂，再利用单调性转化为一般不等式求解．‎ ‎ 3．探究指数型函数的性质与研究一般函数的定义域、单调性(区间)、奇偶性、最值(值域)等性质的方法一致．‎ ‎ 易错警示：在研究指数型函数的单调性时，当底数a与“‎1”‎的大小关系不确定时，要分类讨论．‎