- 2021-06-16 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习小题综合限时练(四)作业(全国通用)
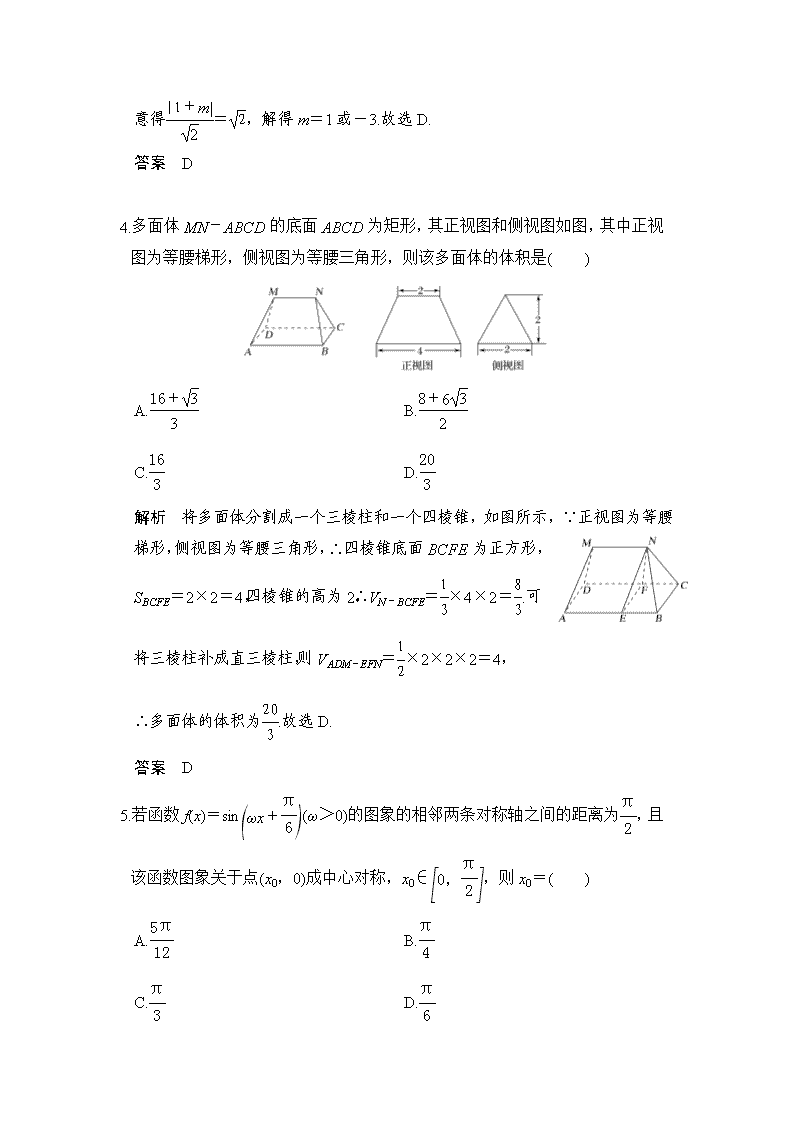
(限时:40分钟) 一、选择题(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合M={x|x2-4x<0},N={x|m<x<5},若M∩N={x|3<x<n},则m+n等于( ) A.9 B.8 C.7 D.6 解析 ∵M={x|x2-4x<0}={x|0<x<4},N={x|m<x<5},且M∩N={x|3<x<n},∴m=3,n=4,∴m+n=3+4=7.故选C. 答案 C 2.《张丘建算经》卷上第22题——“女子织布”问题:某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天共织布390尺,则该女子织布每天增加( ) A.尺 B.尺 C.尺 D.尺 解析 依题意知,每天的织布数组成等差数列,设公差为d,则5×30+d=390,解得d=.故选B. 答案 B 3.已知直线l:x+y+m=0与圆C:x2+y2-4x+2y+1=0相交于A、B两点,若△ABC为等腰直角三角形,则m=( ) A.1 B.2 C.-5 D.1或-3 解析 △ABC为等腰直角三角形,等价于圆心到直线的距离等于圆的半径的.圆C的标准方程是(x-2)2+(y+1)2=4,圆心到直线l的距离d=,依题意得=,解得m=1或-3.故选D. 答案 D 4.多面体MN-ABCD的底面ABCD为矩形,其正视图和侧视图如图,其中正视图为等腰梯形,侧视图为等腰三角形,则该多面体的体积是( ) A. B. C. D. 解析 将多面体分割成一个三棱柱和一个四棱锥,如图所示,∵正视图为等腰梯形,侧视图为等腰三角形,∴四棱锥底面BCFE为正方形,SBCFE=2×2=4,四棱锥的高为2,∴VN-BCFE=×4×2=.可将三棱柱补成直三棱柱,则VADM-EFN=×2×2×2=4, ∴多面体的体积为.故选D. 答案 D 5.若函数f(x)=sin(ω>0)的图象的相邻两条对称轴之间的距离为,且该函数图象关于点(x0,0)成中心对称,x0∈,则x0=( ) A. B. C. D. 解析 由题意得=,T=π,ω=2,又2x0+=kπ(k∈Z),x0=-(k∈Z),而x0∈,∴x0=.故选A. 答案 A 6.已知向量a、b的模都是2,其夹角是60°,又=3a+2b,=a+3b,则P、Q两点间的距离为( ) A.2 B. C.2 D. 解析 ∵a·b=|a|·|b|·cos 60°=2×2×=2,=-=-2a+b,∴||2=4a2-4a·b+b2=12,∴||=2.故选C. 答案 C 7.设双曲线-=1的左、右焦点分别为F1、F2,过F1的直线l交双曲线左支于A、B两点,则|BF2|+|AF2|的最小值为( ) A. B.11 C.12 D.16 解析 由双曲线定义可得|AF2|-|AF1|=2a=4,|BF2|-|BF1|=2a=4,两式相加可得|AF2|+|BF2|=|AB|+8,由于AB为经过双曲线的左焦点与左支相交的弦,而|AB|min==3,∴|AF2|+|BF2|=|AB|+8≥3+8=11.故选B. 答案 B 8.已知函数f(x)=x3+ax2+bx+c,且0查看更多