浙江省嘉兴市2021届高三9月教学测试数学试题

浙江省嘉兴市2021届高三9月教学测试数学试题

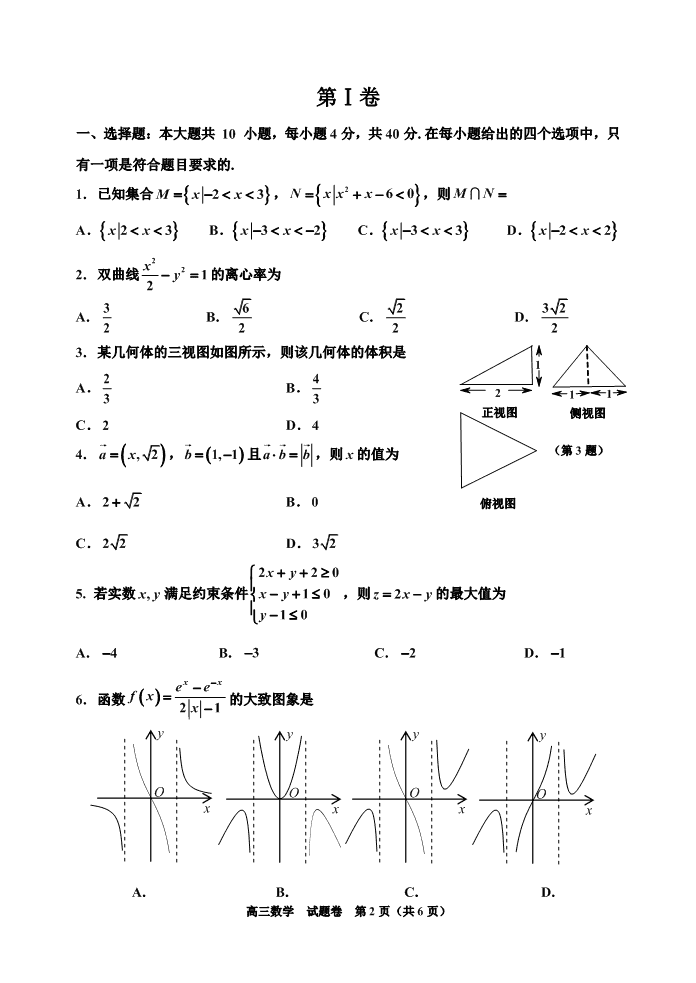
高三数学 试题卷 第 1 页（共 6 页） 2020 年嘉兴市高三教学测试 高三数学 试题卷 （2020.9） 注意事项： 1．本科考试分试题卷和答题卷，考生须在答题卷上作答．答题前，请在答题卷的密 封线内填写学校、班级、学号、姓名; 2．本试题卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 6 页，全卷满 分 150 分，考试时间 120 分钟． 参考公式： 若事件 A，B 互斥，则 )()()( BPAPBAP  若事件 A，B 相互独立，则 )()()( BPAPBAP  若事件 A 在一次试验中发生的概率是 p， 则 n 次独立重复试验中事件 A 恰好发生 k 次的概率 ),,2,1,0()1()( nkppCkP knkk nn   台体的体积公式 hSSSSV )(3 1 2211  其中 21 , SS 分别表示台体的上、下底面积， h 表示台体的高． 柱体的体积公式 ShV  其中 S 表示柱体的底面积， h 表示柱体的 高 锥体的体积公式 ShV 3 1 其中 S 表示锥体的底面积， 表示锥体的 高 球的表面积公式 24 RS  球的体积公式 3 3 4 RV  其中 R 表示球的半径 高三数学 试题卷 第 2 页（共 6 页） 第Ⅰ卷 一、选择题：本大题共 10 小题，每小题 4 分，共 40 分.在每小题给出的四个选项中，只 有一项是符合题目要求的. 1. 已知集合  23M x x    ，  2 60N x x x    ，则 MN A． 23xx B． 32xx    C． 33xx   D． 22xx   2. 双曲线 2 2 12 x y的离心率为 A. 3 2 B. 6 2 C. 2 2 D. 32 2 3. 某几何体的三视图如图所示，则该几何体的体积是 A． 2 3 B． 4 3 C． 2 D． 4 4.  ,2ax ，  1, 1b 且 a b b ，则 x 的值为 A． 22 B． 0 C． 22 D． 32 5. 若实数 ,xy满足约束条件 2 2 0 10 10 xy xy y          ，则 2z x y的最大值为 A. 4 B. 3 C. 2 D. 1 6. 函数   21 xxeefx x   的大致图象是 A. B. C. D. y x O y x O y x O y x O 俯视图 侧视图 正视图 1 1 1 2 （第 3 题） 高三数学 试题卷 第 3 页（共 6 页） 7. 对于函数   2cos 3 sin cos ,f x x x x x R   ，下列命题错误的是 A．函数  fx的最大值是 3 2 B．不存在 54,63   ，使得   1 2f   C．函数 在 ,62   上单调递减 D．存在 10, 3 ，使得    5f x f x   恒成立 8. 数列 na 的前 n 项和为 nS ，且 2 nS n n a   ，nN ，则“ 0a  ”是“数列 2na 为 等差数列”的 A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 9. 如图，矩形 ABCD 中， 1AB  ， 2BC  ，点 E 为 AD 中点，将 ABE 沿 BE 折起， 在翻折过程中，记二面角 A DC B的平面 角大小为 ，则当 最大时， tan  A． 2 2 B． 2 3 C． 1 3 D． 1 2 10. 已知函数     1xf x e a tax   ，其中 0t  .若对于某个 tR ，有且仅有 3 个不同 取值的 a ，使得关于 x 的不等式   0fx 在 R 上恒成立，则 t 的取值范围为 A.  1,e B.  ,2ee C.  ,e  D.  2,e  第Ⅱ卷 二、填空题：本大题有 7 小题，多空题每题 6 分，单空题每题 4 分，共 36 分. 11. 已知  ,z a bi a b R   ，其中 i 为虚数单位.若  21i i z   ，则a  __________; z  __________. A E D B C （第 9 题） A 高三数学 试题卷 第 4 页（共 6 页） 12. 函数  fx是定义在 R 上的奇函数，且当 0x  时，   24xfx，则  1f _____； 不等式   0fx 的解集为___________. 13. 已知  5 26 0 1 2 61 2 1x x a a x a x a x       ，则 2a  ________； 0 1 2 6a a a a     ________. 14. 已知盒中装有  1nn 个红球和 3 个黄球，从中任取 2 个球（取到每个球是等可能的）， 随机变量 X 表示取到黄球的个数，且 的分布列为： 0 1 2 P 1 5 a b 则 n  _________；  EX ________. 15. 已知正项．．等比数列 na 的前 n 项和为 nS ，若 5 1 2 3 4 5 1 1 1 1 116S a a a a a       ，则 3a  ________. 16. 已知直线 :1ly 与 y 轴交于点 M ， Q 为直线 l 上异于 M 的动点，记点Q 的横坐标 为  000xx .若椭圆 2 2 12 x y上存在点 N ，使得 45MQN，则 0x 的取值范围是 _______. 17. 已知不共线向量 a ，b 满足 1ab，且 4a xb a xb    ，向量 a ，b 的夹角为  ，若 14 15 22x ，则 cos 的最小值为_________. X 0 1 2 P a 3 2 b 高三数学 试题卷 第 5 页（共 6 页） 三、解答题：本大题共 5 小题，共 74 分.解答应写出文字说明、证明过程或演算步骤. 18．（本题满分 14 分） 在 ABC 中，角 ,,A B C 所对的边分别是 ,,a b c .已知 2 sin 5 cosb A a B . （1）求cosB 的值； （2）若 3 , 2a c b，求 c 的值. 19．（本题满分 15 分） 如图，四棱锥 A BCDE 中， ABC 为等边三角形，CD  平面 ABC ， BE ∥ CD 且 22AC CD BE   ， F 为 AD 中点. （1）求证： EF ∥平面 ABC ； （2）求直线 BC 与平面 AED 所成角的正弦值. 20．（本题满分 15 分） 已知数列 na 的前 n 项和为 nS ， 2nnS a n， *nN . （1）求数列 的通项公式； （2）令 2nnb na ，求数列 nb 的前 n 项和 nT . C D E F B A （第 19 题） 高三数学 试题卷 第 6 页（共 6 页） 21．（本题满分 15 分） 如图，已知抛物线  2 1 : 2 0C x my m，  2 2 : 2 0C y nx n的焦点分别为 12,FF，且 41mn  . （1）当 12FF 最短时，求直线 12FF的方程； （2）设抛物线 12,CC异于原点的交点为 Q ，过 点Q 作直线 AB ，分别交 于 A ，B 两点，其中直 线 的斜率 0k  ，且 点Q 为线段 的中点.当 AB 最短时，求抛物线 的方程. 22．（本题满分 15 分） 已知函数    2ln 2 0f x x x x ax k k      （1）当 0a  ， 1k  时，求  fx在   1, 1f 处的切线方程； （2）当  0,x  时， 的最小值为 0 ,求 4ka 的最小值. F2 F1 B Q A O x （第 21 题） y