天津市静海区第一中学2019-2020学年高一下学期第第12周周测数学试题

天津市静海区第一中学2019-2020学年高一下学期第第12周周测数学试题

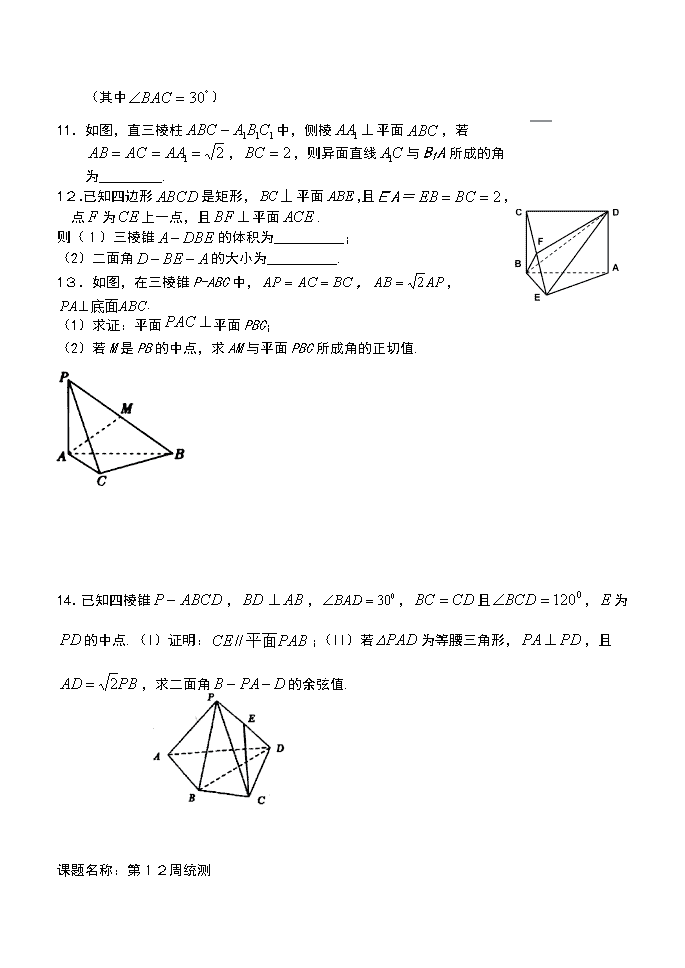
静海区第一中学2019-2020学年高一下学期第第12周周测数学试题 ‎1．若非零向量满足，且，则与的夹角为（ ）‎ A． B． C． D．‎ ‎2．已知非零向量满足，且，则与的夹角为 （ ）‎ A． B． C． D．‎ ‎3．如图，在平面四边形ABCD中，‎ 若点E为边CD上的动点，则的最大值为 （ ）‎ A． B． C． D．‎ ‎4．在中，，则的形状一定是 （ ）‎ A．等边三角形 B．等腰三角形 C．直角三角形 D．等腰直角三角形 ‎5．ABC的三个内角A、B、C所对的边分别为a，b，c，asin AsinB+bcos‎2A=2 ，则（ ）‎ A． B． C． D．‎ ‎6．是虚数单位，复数，那么 （ ）‎ A． B．‎3 ‎C．1 D．‎ ‎7．在梯形中，，，.将梯形绕AB 所在直线旋转一周而形成的曲面所围成的几何体的体积为 （ ）‎ A． B． C． D．‎ ‎8．m，n为异面直线，m⊥平面α，n⊥平面β，直线l满足l⊥m，l ⊥n，则（ ）‎ A．α∥β且∥α B．α⊥β且⊥β C．α与β相交，且交线平行于 D．α与β相交，且交线垂直于 ‎9．已知向量与的夹角为，且，若，且则实数的值为__________．‎ ‎10．如图所示，半径为的半圆内的阴影部分当以直径 所在直线为轴旋转一周时，得到一几何体，则该几何体的表面积是_________，体积是_______.（其中）‎ ‎11．如图，直三棱柱中，侧棱平面，若，，则异面直线与B‎1A所成的角为_________.‎ ‎1２．已知四边形是矩形，平面，且ＥA＝，点为上一点，且平面.‎ 则（１）三棱锥的体积为＿＿＿＿＿；‎ ‎（2）二面角的大小为＿＿＿＿＿.‎ ‎1３．如图，在三棱锥P-ABC中，，，.‎ ‎（1）求证：平面平面PBC；‎ ‎（2）若M是PB的中点，求AM与平面PBC所成角的正切值.‎ ‎14．已知四棱锥，，，且，为的中点.（I）证明：；（II）若为等腰三角形，，且，求二面角的余弦值.‎ 课题名称：第１２周统测 ‎1．若非零向量满足，且，则与的夹角为（B ）‎ A． B． C． D．‎ 解：‎ ‎2．已知非零向量满足，且，则与的夹角为 （ A ）‎ A． B． C． D．‎ 解：‎ ‎3．如图，在平面四边形ABCD中，‎ 若点E为边CD上的动点，则的最大值为 （ D ）‎ A． B． C． D．‎ 解：建系，‎ ‎4．在中，，则的形状一定是 （ C ）‎ A．等边三角形 B．等腰三角形 C．直角三角形 D．等腰直角三角形 ‎5．ABC的三个内角A、B、C所对的边分别为a，b，c，asin AsinB+bcos‎2A=2 ，则（B ）‎ A． B． C． D．‎ ‎6．是虚数单位，复数，那么 （ Ａ ）‎ A． B． ‎3 ‎C．1 D．‎ ‎7．在梯形中，，，.将梯形绕AB 所在直线旋转一周而形成的曲面所围成的几何体的体积为 （ Ｂ ）‎ A． B． C． D．‎ ‎8．m，n为异面直线，m⊥平面α，n⊥平面β，直线l满足l ⊥m，l ⊥n，则（ Ｃ）‎ A．α∥β且∥α B．α⊥β且⊥β C．α与β相交，且交线平行于 D．α与β相交，且交线垂直于 ‎9．已知向量与的夹角为，且，若，且则实数的值为__________．‎ 10． 如图所示，半径为的半圆内的阴影部分当以直径所在直线为轴旋转一周时，得到一几何体，则该几何体的表面积是_________，体积是_______.（其中）‎ ‎11．如图，直三棱柱中，侧棱平面，若，，则异面直线与B‎1A所成的角为_________.‎ ‎1２．已知四边形是矩形，平面，且ＥA＝，点为上一点，且平面.‎ 则（１）三棱锥的体积为＿＿＿＿＿；‎ ‎（2）二面角的大小为＿＿＿＿＿.‎ ‎1３．如图，在三棱锥P-ABC中，，，.‎ ‎（1）求证：平面平面PBC；‎ ‎（2）若M是PB的中点，求AM与平面PBC所成角的正切值.‎ 14． 已知四棱锥，，，且，为的中点.‎ （I） 证明：；‎ （II） 若为等腰三角形，，且，‎ 求二面角的余弦值.‎ 解：（1）思路：取BD的中点为M,连接ME,MC,‎ 证明ＭＥ//平面PAB，MC//平面PAB，MC∩ME=M，‎ 所以平面PAB//平面EMC，所以CE//平面PAB.‎