黑龙江省大庆中学2020-2021高二数学10月月考试题（Word版附答案）

黑龙江省大庆中学2020-2021高二数学10月月考试题（Word版附答案）

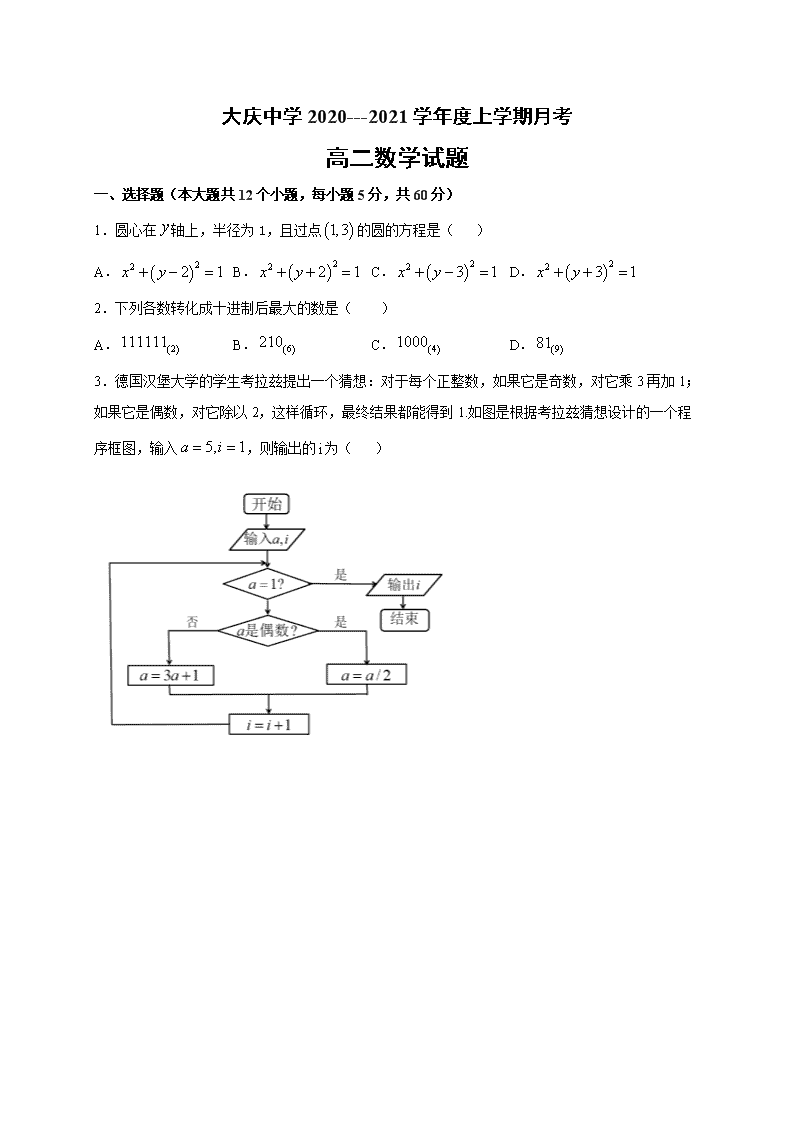
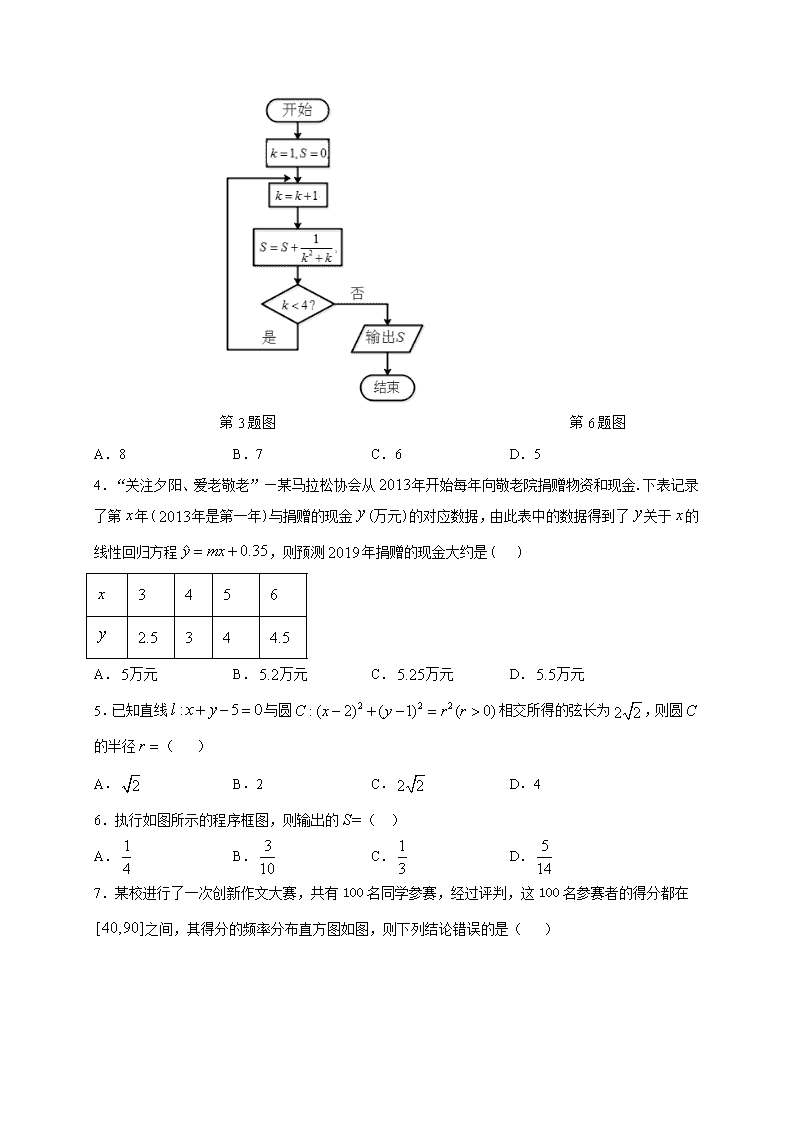
大庆中学2020---2021学年度上学期月考 高二数学试题 ‎ 一、选择题（本大题共12个小题，每小题5分，共60分）‎ ‎1．圆心在轴上，半径为1，且过点的圆的方程是（ ）‎ A． B． C． D．‎ ‎2．下列各数转化成十进制后最大的数是（ ）‎ A． B． C． D．‎ ‎3．德国汉堡大学的学生考拉兹提出一个猜想：对于每个正整数，如果它是奇数，对它乘3再加1；如果它是偶数，对它除以2，这样循环，最终结果都能得到1.如图是根据考拉兹猜想设计的一个程序框图，输入，则输出的为（ ）‎ ‎ ‎ ‎ 第3题图 第6题图 A．8 B．7 C．6 D．5‎ ‎4．“关注夕阳、爱老敬老”—某马拉松协会从年开始每年向敬老院捐赠物资和现金.下表记录了第年(年是第一年)与捐赠的现金(万元)的对应数据，由此表中的数据得到了关于的线性回归方程，则预测年捐赠的现金大约是( )‎ A．万元 B．万元 C．万元 D．万元 ‎5．已知直线与圆相交所得的弦长为，则圆的半径（ ）‎ A． B．2 C． D．4‎ ‎6．执行如图所示的程序框图，则输出的（ ）‎ A． B． C． D．‎ ‎7．某校进行了一次创新作文大赛，共有100名同学参赛，经过评判，这100名参赛者的得分都在之间，其得分的频率分布直方图如图，则下列结论错误的是（ ）‎ ‎ ‎ ‎ 第7题图 第8题图 A．得分在之间的共有40人 B．从这100名参赛者中随机选取1人，其得分在的概率为0.5‎ C．估计得分的众数为55‎ D．这100名参赛者得分的中位数为65‎ ‎8．甲，乙两名同学5次考试的得分如茎叶图所示，其中两竖线之间是得分的十位数．两边分别是甲，乙得分的个位数，则下列结论错误的是（　　）‎ A．甲得分的中位数是85 B．乙得分的中位数与众数相同 C．甲得分的方差小于乙得分的方差 D．甲得分的平均数低于乙得分的平均数 ‎9．直线l：与圆C：交于A，B两点，则当弦AB最短时直线l的方程为（ ）‎ A． B．‎ C． D．‎ ‎10．疫情期间，为了贯彻“停课不停学”的理念，唐老师组织学生参与了一次网络在线考试，并计算出本次考试中全体学生的平均分为85，方差为58；后来有两位学生反应，自己的成绩被登记错误，一位学生的成绩为100分，记录成80分，另一位学生的成绩为70分，记录成90分，唐老师对这两位学生的成绩进行更正后，得到的平均分为，方差为，则（ ）‎ A．， B．，‎ C．， D．，‎ ‎11．如图是一个求20个数的平均数的程序，在横线上应填充的语句为（　　）‎ A． B． C． D．‎ ‎12．设为直线上的动点，、为圆的两条切线，、为切点，则四边形面积的最小值为（ ）‎ A． B． C． D．‎ 第II卷（非选择题）‎ 二、填空题（本大题共4个小题，每小题5分，共20分）‎ ‎13．某事业单位共有职工600人，其年龄与人数分布表如下：‎ 年龄段 人数（单位：人）‎ ‎180‎ ‎180‎ ‎160‎ ‎80‎ 约定：此单位45岁~59岁为中年人，其余为青年人，现按照分层抽样抽取30人作为全市庆祝晚会的观众.则抽出的青年观众有______________人.‎ ‎14．用秦九韶算法求函数，当时的值时，的结果是____________.‎ ‎15．从某小学随机抽取100名学生，将他们的身高（单位：cm）数据绘制成如图所示的频率分布直方图，则身高在[120，130)内的学生人数为______________．‎ ‎16．圆与圆的公 共弦长为_______________．‎ 三、解答题（本大题共6个小题，共70分）‎ ‎17．（本题10分）‎ ‎（文科生做）已知等差数列，若，且，，成等比数列．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若，设，求数列的前项和．‎ ‎（理科生做）已知等比数列的公比，且的等差中项为10， .‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设， 求数列的前项和.‎ ‎18．（本题12分）在中，角，，所对的边分别是，，，且.‎ ‎（1）求的值；‎ ‎（2）若的面积为，且，求的值.‎ ‎19．（本题12分）疫情期间，在家中适当锻炼，合理休息，能够提高自身免疫力，抵抗病毒.某小区为了调查“宅”家居民的运动情况，从该小区随机抽取了100位居民，记录了他们某天的锻炼时间，其频率分布直方图如下：‎ ‎（1）求的值，并求众数的估计值；‎ ‎（2）估计这100位居民锻炼时间的平均值；（同一组中的数据用该组区间的中点值代表）‎ ‎（3）求中位数的估计值.‎ ‎20．（本题12分）已知圆，为坐标原点，动点在圆外，过作圆的切线，设切点为.‎ ‎（1）若点运动到处，求此时切线的方程；‎ ‎（2）求满足条件的点的轨迹方程.‎ ‎21．（本题12分）如图，四棱锥的底面为菱形，，，分别为和的中点．‎ ‎（）求证：平面．‎ ‎（）求证：平面．‎ ‎22．（本题12分）学生甲在一次试验中用显微镜观察某种环境下细菌的个数，发现时间x（分钟）时刻的细菌个数为y个，统计结果如下：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ y ‎2‎ ‎3‎ ‎4‎ ‎4‎ ‎5‎ ‎（Ⅰ）在给出的坐标系中画出x，y的散点图，说明细菌个数和时间是正相关还是负相关.‎ ‎（Ⅱ）根据表格中的5组数据，求y关于x的回归直线方程，并根据回归直线方程估计从实验开始，什么时刻细菌个数为12.‎ 参考公式：（）‎ 大庆中学2020---2021学年度上学期月考 高二数学 答案 ‎1．C 2．B 3．C 4．C 5．B 6．B ‎ ‎7．D 8．C 9．A 10．A 11．B 12．B ‎13．18 14．6 15． 16．‎ ‎17．（文科）解：（Ⅰ）∵，∴①‎ ‎∵，，成等比数列，∴，‎ ‎∴化简得，‎ 若，‎ 若，②，由①②可得，，‎ 所以数列的通项公式是或 -------------------5分 ‎（Ⅱ）由（Ⅰ）得 ‎∴ ----------------------10分 ‎（理科）解：（Ⅰ）由题意可得：， ‎ ‎ ∴ ‎ ‎∵，∴，‎ ‎∴数列的通项公式为.-------------------5分 ‎（Ⅱ） ， ‎ ‎∴‎ ‎ ‎ 上述两式相减 可得 ‎ ‎∴=---------------10分 ‎18．解：（1）∵，‎ ‎∴，‎ 即 ； -------------------6分 ‎（2） ，‎ ‎ . ------------10分 ‎19．解：（1）由题意，得 ‎.解得. ‎ 众数的估计值为 （分钟） ----------------4分 ‎（2）估计这100位居民锻炼时间的平均值 ‎（分钟）. ----------------8分 ‎（3）设中位数的估计值为.‎ 由，‎ 得，所以中位数的估计值为. ----------------12分 ‎20．解：（1）‎ 切线斜率不存在时，即，满足圆心到切线距离等于半径，‎ 当切线斜率存在时，设 综上，切线的方程为或； -----------------------6分 ‎（2）设，则由得 ‎ ----------------------12分 ‎21．解：（）证明：取中点为，‎ ‎∵在中，是中点，是中点，‎ ‎∴，且，‎ 又∵底面是菱形，‎ ‎∴，‎ ‎∵是中点，‎ ‎∴，且，‎ ‎∴，且，‎ ‎∴四边形是平行四边形，‎ ‎∴，‎ 又平面，平面，‎ ‎∴平面． ----------------------------6分 ‎（）证明：设，则是中点，‎ ‎∵底面是菱形，‎ ‎∴，‎ 又∵，是中点，‎ ‎∴，‎ 又，‎ ‎∴平面． -----------------------12分 ‎22． 解：（Ⅰ）图形如下，观察图像可知细菌个数和时间是正相关.‎ ‎ -----------------2分 ‎（Ⅱ）由数据计算得，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎， ‎ 所以， ---------------10分 当时，解得.‎ 所以当时细菌个数为12个. -----------------------12分