- 2021-06-16 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江西省景德镇一中2021届高三8月月考数学(理)试题 Word版含答案
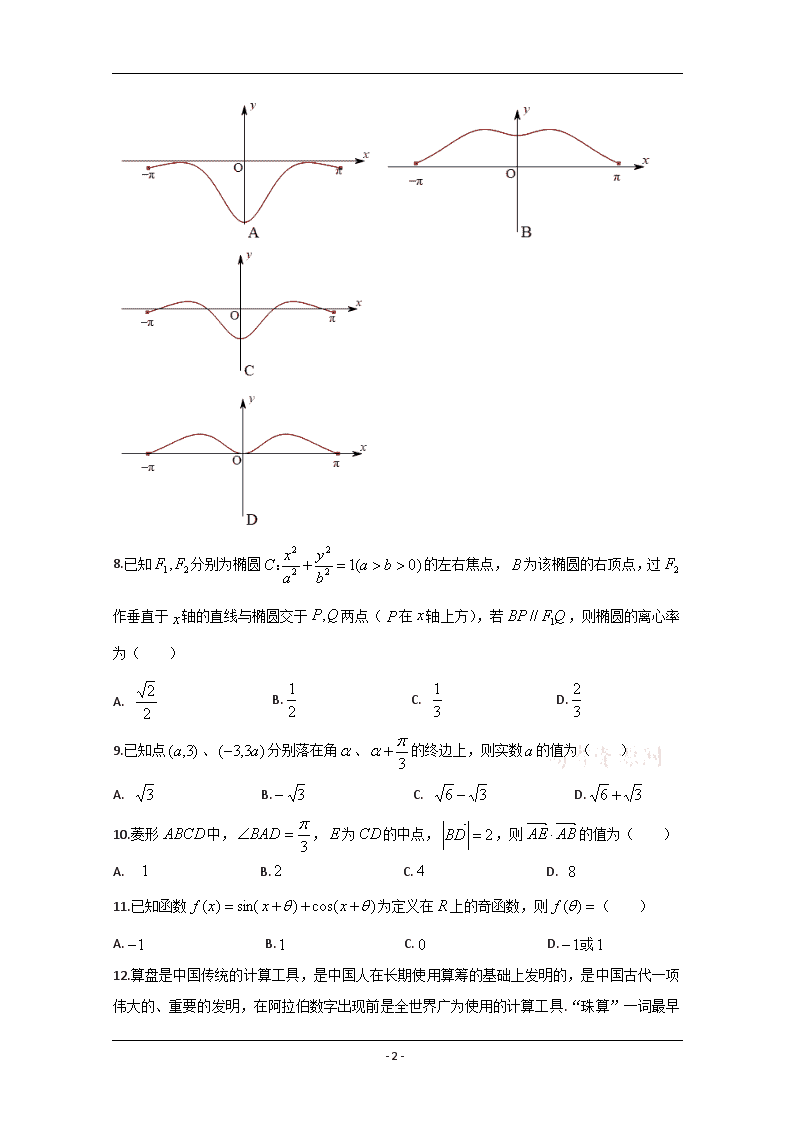
景德镇一中2021届高三8月月考理科数学试卷 一、选择题:本题12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,,则( ) A. B. C. D. 2.设,为虚数单位,若复数为纯虚数,则( ) A. B. C. D. 3. 已知一组数据的茎叶图如图所示,则下列说法正确的是( ) ①该组数据的中位数为;②该组数据的极差为; ③将该组数据中每个数据都加上,得到的新的一组数据的方差与该组数据的方差相同; A. ① B.①③ C.②③ D.①②③ 4. 理查德·赫恩斯坦 [(Richard J. Herrnstein ),美国比较心理学家]和默瑞(Charles Murray)合著《正态曲线》一书而闻名,在该书中他们指出人们的智力呈正态分布。假设犹太人的智力服从正态分布,从犹太人中任选一个人智力落在以上的概率为(附:若随机变量服从正态分布,则,( ) A. B. C. D. 5. 函数的零点个数为( ) A. B. C. D. 6.若, 则 ( ) A. B. C. D. 7.函数在的图像大致是( ) - 8 - 8.已知分别为椭圆的左右焦点,为该椭圆的右顶点,过作垂直于轴的直线与椭圆交于两点(在轴上方),若,则椭圆的离心率为( ) A. B. C. D. 9.已知点、分别落在角、的终边上,则实数的值为( ) A. B. C. D. 10.菱形中,,为的中点,,则的值为( ) A. B. C. D. 11.已知函数为定义在上的奇函数,则( ) A. B. C. D.或 12.算盘是中国传统的计算工具,是中国人在长期使用算筹的基础上发明的,是中国古代一项伟大的、重要的发明,在阿拉伯数字出现前是全世界广为使用的计算工具.“珠算” - 8 - 一词最早见于东汉徐岳所撰的《数术记遗》,其中有云:“珠算控带四时,经纬三才。”北周甄鸾为此作注,大意是:把木板刻为3部分,上、下两部分是停游珠用的,中间一部分是作定位用的。右图是一把算盘的初始状态,自右向左,分别是个位、十位、百位……,上面一粒珠(简称上珠)代表5,下面一粒珠(简称下珠)是1,即五粒下珠的大小等于同组一粒上珠的大小。现在从个位和十位这两组中随机选择往下拨一粒上珠,往上拨2粒下珠,算盘表示的数为质数(除了1和本身没有其它的约数)的概率是( ) A. B. C. D. 二、 填空题:本题共4小题,每小题5分,共20分. 13.已知函数函数在处取极值,则 . 14.已知数列是公差的等差数列,的前项和为,,,则 . 15.在新型冠状病毒Covid-19爆发期间,前期主要是通过对疑似病例的血液标本或呼吸道标本进行荧光RT-PCR检查,只要有一次检测显示为新型冠状核酸阳性则判断该疑似病例为确诊病例.但是由于新型冠状病毒是“流氓”病毒,检测标本中即使含有新型冠状病毒,一次荧光RT-PCR检查结果为阳性的概率也只有,故需要对疑似病例多次采集标本进行检测.现对某确诊病例先后采集次标本进行荧光RT-PCR检查,假设每次检查是否为新型冠状核酸阳性相互独立,则3次检查结果中仅有次为阳性的概率为 . 16.已知分别为的角的对边,,则角大小为 . 三、 解答题:共70分.解答应写出文字说明、证明过程或演算步骤(17题10分,其余12分). 17.曲线的参数方程为(为参量),曲线的参数方程为,(为参量). - 8 - (1) 求曲线和的极坐标方程; (2) 若射线:与曲线和分别交于两点,当时,求的值. 18.已知数列的前项和. (1)若,求数列的通项公式; (2)是否存在实数使得数列为等比数列?若存在,求出实数的值;若不存在,请说明理由. 19.近年来,“双11”网购的观念逐渐深入人心.某人统计了近年某网站“双11”当天的交易额,统计结果如下表. 年份 2015 2016 2017 2018 2019 年份代码 1 2 3 4 5 交易额/百亿元 9 12 17 21 26 (1) 请根据上表提供的数据,用相关系数说明与的线性相关程度(线性相关系数保留三位小数); (2) 求出关于的线性回归方程,并预测年该网站“双11”当天的交易额. 参考公式:,; - 8 - 相关系数 ;参考数据:. 20.如图,四棱锥中,,为的中点,且. (1)证明:平面; (2)求平面与平面夹角的余弦值. 21.已知点为曲线的焦点,点在曲线运动,当点运动到轴上方且满足轴时,点到直线的距离为. (1) 求曲线的方程; (2) 设过点的直线与曲线交于两点,则在轴上是否存在一点,使得直线与直线关于轴对称?若存在,求出点的坐标;若不存在,请说明理由. 22.已知函数. (1) 当时,判断函数的单调性; (2) 若函数有两个极值点,且,证明:. - 8 - 参考答案 1-5 CBDAA 6-10 CCCAC 11-12 AA 13. 14. 15. 16. - 8 - - 8 - - 8 -查看更多