【数学】2019届一轮复习全国经典版（理）直线、平面垂直的判定及性质学案

【数学】2019届一轮复习全国经典版（理）直线、平面垂直的判定及性质学案

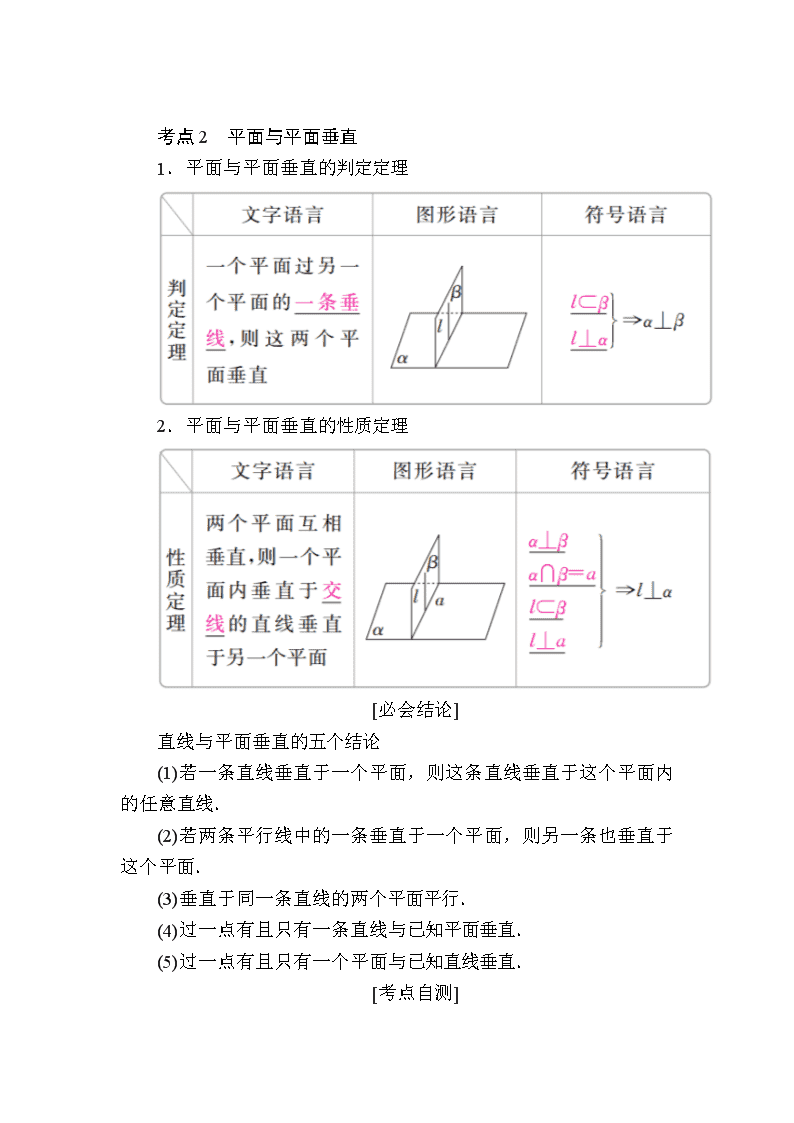
第5讲　直线、平面垂直的判定及性质 板块一　知识梳理·自主学习 ‎[必备知识]‎ 考点1　直线与平面垂直 ‎1．直线和平面垂直的定义 直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直．‎ ‎2．直线与平面垂直的判定定理 ‎3．直线与平面垂直的性质定理 考点2　平面与平面垂直 ‎1．平面与平面垂直的判定定理 ‎2．平面与平面垂直的性质定理 ‎[必会结论]‎ 直线与平面垂直的五个结论 ‎(1)若一条直线垂直于一个平面，则这条直线垂直于这个平面内的任意直线．‎ ‎(2)若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．‎ ‎(3)垂直于同一条直线的两个平面平行．‎ ‎(4)过一点有且只有一条直线与已知平面垂直．‎ ‎(5)过一点有且只有一个平面与已知直线垂直．‎ ‎[考点自测]‎ ‎1．判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)垂直于同一个平面的两平面平行．(　　)‎ ‎(2)若两条直线与一个平面所成的角相等，则这两条直线平行．(　　)‎ ‎(3)若平面α内的一条直线垂直于平面β内的无数条直线，则α⊥β.(　　)‎ ‎(4)二面角是指两个相交平面构成的图形．(　　)‎ ‎(5)若两个平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面．(　　)‎ 答案　(1)×　(2)×　(3)×　(4)×　(5)×‎ ‎2．[2018·浙江模拟]设m，n是两条不同的直线，α，β是两个不同的平面，下列命题正确的是(　　)‎ A．若m⊥n，n∥α，则m⊥α B．若m∥β，β⊥α，则m⊥α C．若m⊥β，n⊥β，n⊥α，则m⊥α D．若m⊥n，n⊥β，β⊥α，则m⊥α 答案　C 解析　对于选项A，B，D，均能举出m⊥α的反例；对于选项C，若m⊥β，n⊥β，则m∥n，又n⊥α，∴m⊥α.故选C.‎ ‎3．[课本改编]若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是(　　)‎ A．若m⊂β，α⊥β，则m⊥α B．若α∩γ＝m，β∩γ＝n，m∥n，则α∥β C．若m⊥β，m∥α，则α⊥β D．若α⊥γ，α⊥β，则β⊥γ 答案　C 解析　A中m与α的位置关系不确定，故错误；B中α，β可能平行或相交，故错误；由面面垂直的判定定理可知C正确；D中β，γ平行或相交 ，所以D错误．故选C.‎ ‎4．在如图所示的四个正方体中，能得出AB⊥CD的是(　　)‎ 答案　A 解析　A中，CD⊥AB；B中，AB与CD成60°角；C中，AB与CD成45°角；D中，AB与CD夹角的正切值为.故选A.‎ 板块二　典例探究·考向突破 考向　有关垂直关系的判断 例　1　[2017·广州模拟]设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是(　　)‎ A．若α⊥β，m⊂α，n⊂β，则m⊥n B．若m⊥α，m∥n，n∥β，则α⊥β C．若m⊥n，m⊂α，n⊂β，则α⊥β D．若α∥β，m⊂α，n⊂β，则m∥n 答案　B 解析　若α⊥β，m⊂α，n⊂β，则m与n相交、平行或异面，故A错误；‎ ‎∵m⊥α，m∥n，∴n⊥α，又∵n∥β，∴α⊥β，故B正确；‎ 若m⊥n，m⊂α，n⊂β，则α与β的位置关系不确定，故C错误；‎ 若α∥β，m⊂α，n⊂β，则m∥n或m，n异面，故D错误．故选B.‎ 触类旁通 判断垂直关系需注意的问题 ‎(1)作图要熟练，借助几何图形来说明线面关系要做到作图快、准．‎ ‎(2)善于寻找反例，若存在反例，结论就被驳倒了．‎ ‎(3)要思考完整，反复验证所有可能的情况，必要时要运用判定或性质定理进行简单说明．‎ ‎【变式训练1】　[2018·北京东城模拟]已知m和n是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m⊥β的是(　　)‎ A．α⊥β，且m⊂α B．m∥n，且n⊥β C．α⊥β，且m∥α D．m⊥n，且n∥β 答案　B 解析　因为α⊥β，m⊂α，则m，β的位置关系不确定，可能平行、相交、m在β面内，故A错误；由线面垂直的性质定理可知B正确；若α⊥β，m∥α，则m，β的位置关系也不确定，故C错误；若m⊥n，n∥β，则m，β的位置关系也不确定，故D错误．故选B.‎ 考向　直线与平面垂直的判定与性质 命题角度1　利用线线垂直证明线面垂直 例　2　[2018·湖北宜昌模拟]在正三棱柱ABC－A1B1C1中，BC＝BB1，E，F，M分别为A1C1，AB1，BC的中点．‎ ‎(1)求证：EF∥平面BB1C1C；‎ ‎(2)求证：EF⊥平面AB1M.‎ 证明　(1)连接A1B，BC1.‎ 因为E，F分别为A1C1，AB1的中点，‎ 所以F为A1B的中点，所以EF∥BC1.‎ 因为BC1⊂平面BB1C1C，EF⊄平面BB1C1C，‎ 所以EF∥平面BB1C1C.‎ ‎(2)在矩形BCC1B1，BC＝BB1，‎ 所以tan∠CBC1＝，tan∠B1MB＝.‎ 所以tan∠CBC1·tan∠B1MB＝1.‎ 所以∠CBC1＋∠B1MB＝.所以BC1⊥B1M.‎ 因为EF∥BC1，所以EF⊥B1M.‎ 在正三棱柱ABC－A1B1C1中，底面ABC⊥平面BB1C1C.‎ 因为M为BC的中点，AB＝AC，所以AM⊥BC.‎ 因为平面ABC∩平面BB1C1C＝BC，‎ 所以AM⊥平面BB1C1C.‎ 因为BC1⊂平面BB1C1C，所以AM⊥BC1‎ 因为EF∥BC1，所以EF⊥AM.‎ 又因为AM∩B1M＝M，AM⊂平面AB1M，B1M⊂平面AB1M，所以EF⊥平面AB1M.‎ 命题角度2　利用线面垂直证明线线垂直 例　3　[2017·江苏高考]如图，在三棱锥A－BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD.‎ 求证：(1)EF∥平面ABC；‎ ‎(2)AD⊥AC.‎ 证明　(1)在平面ABD内，因为AB⊥AD，EF⊥AD，‎ 所以EF∥AB.‎ 又因为EF⊄平面ABC，AB⊂平面ABC，‎ 所以EF∥平面ABC.‎ ‎(2)因为平面ABD⊥平面BCD，‎ 平面ABD∩平面BCD＝BD，‎ BC⊂平面BCD，BC⊥BD，‎ 所以BC⊥平面ABD.‎ 因为AD⊂平面ABD，所以BC⊥AD.‎ 又AB⊥AD，BC∩AB＝B，AB⊂平面ABC，BC⊂平面ABC，‎ 所以AD⊥平面ABC.‎ 又因为AC⊂平面ABC，‎ 所以AD⊥AC.‎ 触类旁通 证明线面垂直的常用方法及关键 ‎(1)证明直线和平面垂直的常用方法有：①判定定理；②垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；③面面平行的性质(a⊥α，α∥β⇒a⊥β)；④面面垂直的性质．‎ ‎(2)证明线面垂直的关键是证线线垂直，而证明线线垂直则需借助线面垂直的性质．‎ 考向　面面垂直的判定与性质 例　4　[2016·北京高考]如图，在四棱锥P－ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.‎ ‎(1)求证：DC⊥平面PAC；‎ ‎(2)求证：平面PAB⊥平面PAC；‎ ‎(3)设点E为AB的中点，在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．‎ 解　(1)证明：因为PC⊥平面ABCD，‎ 所以PC⊥DC.‎ 又因为DC⊥AC，且PC∩AC＝C，‎ 所以DC⊥平面PAC.‎ ‎(2)证明：因为AB∥DC，DC⊥AC，‎ 所以AB⊥AC.‎ 因为PC⊥平面ABCD，所以PC⊥AB.‎ 又因为PC∩AC＝C，所以AB⊥平面PAC.‎ 又AB⊂平面PAB，所以平面PAB⊥平面PAC.‎ ‎(3)棱PB上存在点F，使得PA∥平面CEF.‎ 理由如下：取PB的中点F，连接EF，CE，CF.‎ 又因为E为AB的中点，所以EF∥PA.‎ 又因为PA⊄平面CEF，且EF⊂平面CEF，‎ 所以PA∥平面CEF.‎ 触类旁通 判定面面垂直的方法 ‎(1)面面垂直的定义；‎ ‎(2)面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．‎ ‎【变式训练2】　如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AB∥CD，AB⊥BC，DC＝BC＝AB＝1，点M在线段EC上．‎ ‎(1)证明：平面BDM⊥平面ADEF；‎ ‎(2)若AE∥平面MDB，求三棱锥E－BDM的体积．‎ 解　(1)证明：∵DC＝BC＝1，DC⊥BC，∴BD＝.‎ 在梯形ABCD中，AD＝，AB＝2，‎ ‎∴AD2＋BD2＝AB2，∴∠ADB＝90°.‎ ‎∴AD⊥BD.‎ 又平面ADEF⊥平面ABCD，‎ 平面ADEF∩平面ABCD＝AD，‎ ‎∴BD⊥平面ADEF.‎ 又BD⊂平面BDM，‎ ‎∴平面BDM⊥平面ADEF.‎ ‎(2)如图，连接AC，AC∩BD＝O，连接MO，‎ ‎∵平面EAC∩平面MBD＝MO，AE∥平面MDB，AE⊂平面EAC，‎ ‎∴AE∥OM.‎ 又AB∥CD，∴＝＝＝2，‎ S△EDM＝S△EDC＝××1×＝.‎ ‎∵ADEF为正方形，‎ ‎∴ED⊥AD.‎ 又∵平面ADEF⊥平面ADCB，‎ ‎∴ED⊥平面ABCD，BC⊂平面ABCD，∴DE⊥BC.‎ ‎∵AB∥CD，AB⊥BC，∴BC⊥CD.‎ 又ED∩DC＝D，∴BC⊥平面EDC.‎ ‎∴VE－BDM＝VB－EDM＝S△EDM·BC＝××1＝.‎ 核心规律 转化思想：垂直关系的转化 在证明两平面垂直时一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决．‎ 满分策略 ‎1.在用线面垂直的判定定理证明线面垂直时，考生易忽视说明平面内的两条直线相交，而导致被扣分，这一点在证明中要注意．口诀：线不在多，重在相交．‎ ‎2.面面垂直的性质定理是作辅助线的一个重要依据．我们要作一个平面的一条垂线，通常是先找这个平面的一个垂面，在这个垂面中，作交线的垂线即可.‎ 板块三　启智培优·破译高考 题型技法系列12——等体积法求点到平面的距离 ‎[2018·内蒙古模拟]如图，在直三棱柱ABC－DEF中，底面ABC的棱AB⊥BC，且AB＝BC＝2.点G，H在侧棱CF上，且CH＝HG＝GF＝1.‎ ‎(1)证明：EH⊥平面ABG；‎ ‎(2)求点C到平面ABG的距离．‎ 解题视点　(1)证明直线与平面垂直的常用方法为证明直线与平面内的两条相交直线都垂直；(2)等体积法是求解点到平面的距离的常用方法．‎ 解　(1)证明：∵ABC－DEF是直三棱柱，‎ ‎∴FC⊥平面ABC，而AB⊂平面ABC，∴FC⊥AB.‎ 又∵AB⊥BC，BC∩FC＝C.‎ ‎∴AB⊥平面BCFE，‎ 又∵EH⊂平面BCFE，∴AB⊥EH.‎ 由题设知△EFH与△BCG均为直角三角形，‎ ‎∵EF＝2＝FH，BC＝2＝CG，‎ ‎∴∠EHF＝45°，∠BGC＝45°.‎ 设BG∩EH＝P，则∠GPH＝90°，即EH⊥BG.‎ 又AB∩BG＝B，∴EH⊥平面ABG.‎ ‎(2)∵AB＝BC＝2，AB⊥BC，‎ ‎∴S△ABC＝AB×BC＝2.‎ ‎∵CG⊥平面ABC，∴VG－ABC＝S△ABC×CG＝.‎ 由(1)知AB⊥BG，CG＝2＝BC，‎ BG＝＝＝2，‎ ‎∴S△ABG＝AB×BG＝2.‎ 设点C到平面ABG的距离为h，则 ‎∴VC－ABG＝S△ABG·h＝h＝VG－ABC＝，‎ ‎∴h＝.‎ 即点C到平面ABG的距离为.‎ 答题启示　(1)证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质；(2)用等体积法求点到平面距离时，通过换顶点和底面转化为底面积和高易求的锥体体积是关键.‎ 跟踪训练 已知三棱锥A－BCD中，△ABC是等腰直角三角形，且AC⊥BC，BC＝2，AD⊥平面BCD，AD＝1.‎ ‎(1)求证：平面ABC⊥平面ACD；‎ ‎(2)若E为AB的中点，求点A到平面CED的距离．‎ 解　(1)证明：因为AD⊥平面BCD，BC⊂平面BCD，所以AD⊥BC，又因为AC⊥BC，AC∩AD＝A，所以BC⊥平面ACD，BC⊂平面ABC，所以平面ABC⊥平面ACD.‎ ‎(2)由已知可得CD＝，取CD中点为F，连接EF，由于ED＝EC＝AB＝，所以△ECD为等腰三角形，从而EF＝，S△ECD＝，由(1)知BC⊥平面ACD，所以E到平面ACD的距离为1，S△ACD＝，令 A到平面CED的距离为d，有VA－ECD＝·S△ECD·d＝VE－ACD＝·S△ACD·1，解得d＝.‎ 板块四　模拟演练·提能增分 ‎ [A级　基础达标]‎ ‎1．[2016·浙江高考]已知互相垂直的平面α，β交于直线l.若直线m，n满足m∥α，n⊥β，则(　　)‎ A．m∥l B．m∥n C．n⊥l D．m⊥n 答案　C 解析　∵α∩β＝l，∴l⊂β，∵n⊥β，∴n⊥l.故选C.‎ ‎2．[2015·福建高考]若l，m是两条不同的直线，m垂直于平面α，则“l⊥m”是“l∥α”的(　　)‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 答案　B 解析　由“m⊥α且l⊥m”推出“l⊂α或l∥α”，但由“m⊥α且l∥α”可推出“l⊥m”，所以“l⊥m”是“l∥α”的必要而不充分条件，故选B.‎ ‎3．[2017·天津河西模拟]设l是直线，α，β是两个不同的平面，则下列说法正确的是(　　)‎ A．若l∥α，l∥β，则α∥β B．若l∥α，l⊥β，则α⊥β C．若α⊥β，l⊥α，则l∥β D．若α⊥β，l∥α，则l⊥β 答案　B 解析　对于A，若l∥α，l∥β，则α∥β或α与β相交，故A错误；易知B正确；对于C，若α⊥β，l⊥α，则l∥β或l⊂β，故C错误；对于D，若α⊥β，l∥α，则l与β的位置关系不确定，故D错误．故选B.‎ ‎4．[2018·济南模拟]已知如图，六棱锥P－ABCDEF的底面是正六边形，PA⊥平面ABCDEF.则下列结论不正确的是(　　)‎ A．CD∥平面PAF B．DF⊥平面PAF C．CF∥平面PAB D．CF⊥平面PAD 答案　D 解析　A中，因为CD∥AF，AF⊂平面PAF，CD⊄平面PAF，所以CD∥平面PAF成立；‎ B中，因为ABCDEF为正六边形，所以DF⊥AF，‎ 又因为PA⊥平面ABCDEF，所以PA⊥DF，‎ 又因为PA∩AF＝A，所以DF⊥平面PAF成立；‎ C中，因为CF∥AB，AB⊂平面PAB，CF⊄平面PAB，所以CF∥平面PAB；而D中CF与AD不垂直．故选D.‎ ‎5．已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(　　)‎ A．α∥β且l∥α B．α⊥β且l⊥β C．α与β相交，且交线垂直于l D．α与β相交，且交线平行于l 答案　D 解析　若α∥β，则m∥n，这与m、n为异面直线矛盾，所以A不正确，α与β相交．将已知条件转化到正方体中，易知α与β不一定垂直，但α与β的交线一定平行于l，从而排除B，C.故选D.‎ ‎6．已知P为△ABC所在平面外一点，且PA，PB，PC 两两垂直，则下列命题：‎ ‎①PA⊥BC；②PB⊥AC；③PC⊥AB；④AB⊥BC.‎ 其中正确的个数是________．‎ 答案　3‎ 解析　如图所示．∵PA⊥PC，PA⊥PB，PC∩PB＝P，∴PA⊥平面PBC.‎ 又∵BC⊂平面PBC，∴PA⊥BC.同理PB⊥AC，PC⊥AB.‎ 但AB不一定垂直于BC.‎ ‎7．设a，b为不重合的两条直线，α，β为不重合的两个平面，给出下列命题：‎ ‎①若a∥α，b∥β，且α∥β，则a∥b；‎ ‎②若a⊥α，且a⊥β，则α∥β；‎ ‎③若α⊥β，则一定存在平面γ，使得γ⊥α，γ⊥β；‎ ‎④若α⊥β，则一定存在直线l，使得l⊥α，l∥β.‎ 上面命题中，所有真命题的序号是________．‎ 答案　②③④‎ 解析　①中a与b可能相交或异面，故不正确．②垂直于同一直线的两平面平行，正确．③中存在γ，使得γ与α，β都垂直．④中只需直线l⊥α且l⊄β就可以．‎ ‎8．[2018·广东模拟]如图，在三棱锥D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列命题中正确的有________(写出全部正确命题的序号)．‎ ‎①平面ABC⊥平面ABD；‎ ‎②平面ABD⊥平面BCD；‎ ‎③平面ABC⊥平面BDE，且平面ACD⊥平面BDE；‎ ‎④平面ABC⊥平面ACD，且平面ACD⊥平面BDE.‎ 答案　③‎ 解析　由AB＝CB，AD＝CD知AC⊥DE，AC⊥BE，从而AC⊥平面BDE，故③正确．‎ ‎9．如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．求证：‎ ‎(1)CD⊥AE；‎ ‎(2)PD⊥平面ABE.‎ 证明　(1)∵PA⊥底面ABCD，CD⊂平面ABCD，‎ ‎∴CD⊥PA.‎ 又CD⊥AC，PA∩AC＝A，‎ 故CD⊥平面PAC，AE⊂平面PAC.‎ 故CD⊥AE.‎ ‎(2)∵PA＝AB＝BC，∠ABC＝60°，故PA＝AC.‎ ‎∵E是PC的中点，故AE⊥PC.‎ 由(1)知CD⊥AE，由于PC∩CD＝C，‎ 从而AE⊥平面PCD，故AE⊥PD.‎ 易知BA⊥PD，故PD⊥平面ABE.‎ ‎10．[2018·湖南永州模拟]如图，四棱锥S－ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB＝BC＝2，CD＝SD＝1.‎ ‎(1)证明：SD⊥平面SAB；‎ ‎(2)求四棱锥S－ABCD的高．‎ 解　(1)证明：如图，取AB的中点E，连接DE，DB，‎ 则四边形BCDE为矩形，‎ ‎∴DE＝CB＝2，‎ ‎∴AD＝BD＝.‎ ‎∵侧面SAB为等边三角形，AB＝2，‎ ‎∴SA＝SB＝AB＝2.‎ 又SD＝1，‎ ‎∴SA2＋SD2＝AD2，SB2＋SD2＝BD2，‎ ‎∴∠DSA＝∠DSB＝90°，即SD⊥SA，SD⊥SB，SA∩SB＝S，‎ ‎∴SD⊥平面SAB.‎ ‎(2)设四棱锥S－ABCD的高为h，则h也是三棱锥S－ABD 的高．‎ 由(1)，知SD⊥平面SAB.‎ 由VS－ABD＝VD－SAB，得S△ABD·h＝S△SAB·SD，‎ ‎∴h＝.‎ 又S△ABD＝AB·DE＝×2×2＝2，‎ S△SAB＝AB2＝×22＝，SD＝1，‎ ‎∴h＝＝＝.‎ 故四棱锥S－ABCD的高为.‎ ‎[B级　知能提升]‎ ‎1．[2018·青岛质检]设a，b是两条不同的直线，α，β是两个不同的平面，则能得出a⊥b的是(　　)‎ A．a⊥α，b∥β，α⊥β B．a⊥α，b⊥β，α∥β C．a⊂α，b⊥β，α∥β D．a⊂α，b∥β，α⊥β 答案　C 解析　对于C项，由α∥β，a⊂α可得a∥β，又b⊥β，得a⊥b.故选C.‎ ‎2．[2018·河北唐山模拟]如图，在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点，现在沿AE，AF及EF把这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H，那么，在这个空间图形中必有(　　)‎ A．AG⊥平面EFH B．AH⊥平面EFH C．HF⊥平面AEF D．HG⊥平面AEF 答案　B 解析　根据折叠前、后AH⊥HE，AH⊥HF不变，‎ ‎∴AH⊥平面EFH，B正确；∵过A只有一条直线与平面EFH垂直，∴A不正确；∵AG⊥EF，EF⊥GH，AG∩GH＝G，∴EF⊥平面HAG，又EF⊂平面AEF，∴平面HAG⊥平面AEF，过H作直线垂直于平面AEF，一定在平面HAG内，∴C不正确；由条件证不出HG⊥平面AEF，∴D不正确．故选B.‎ ‎3．如图，PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC，其中真命题的序号是________．‎ 答案　①②④‎ 解析　①AE⊂平面PAC，BC⊥AC，BC⊥PA⇒AE⊥BC，故①正确；②AE⊥PC，AE⊥BC⇒AE⊥平面PBC，PB⊂平面PBC⇒AE⊥PB，AF⊥PB，EF⊂平面AEF⇒EF⊥PB，故②正确；③若AF⊥BC⇒AF⊥平面PBC，则AF∥AE与已知矛盾，故③错误；由②可知④‎ 正确．‎ ‎4．[2018·江西九江模拟]如图，在几何体ABCDEF中，四边形ABCD是菱形，BE⊥平面ABCD，DF∥BE，且DF＝2BE＝2，EF＝3.‎ ‎(1)证明：平面ACF⊥平面BEFD.‎ ‎(2)若cos∠BAD＝，求几何体ABCDEF的体积．‎ 解　(1)证明：∵四边形ABCD是菱形，‎ ‎∴AC⊥BD，‎ ‎∵BE⊥平面ABCD，AC⊂平面ABCD，‎ ‎∴BE⊥AC.‎ ‎∴AC⊥平面BEFD，AC⊂平面ACF.‎ ‎∴平面ACF⊥平面BEFD.‎ ‎(2)设AC与BD的交点为O，AB＝a(a>0)，‎ 由(1)得AC⊥平面BEFD，‎ ‎∵BE⊥平面ABCD，∴BE⊥BD，‎ ‎∵DF∥BE，∴DF⊥BD，‎ ‎∴BD2＝EF2－(DF－BE)2＝8，∴BD＝2，‎ ‎∴S四边形BEFD＝(BE＋DF)·BD＝3，‎ ‎∵cos∠BAD＝，‎ ‎∴BD2＝AB2＋AD2－2AB·AD·cos∠BAD＝a2＝8，‎ ‎∴a＝，‎ ‎∴OA2＝AB2－OB2＝3，∴OA＝，‎ ‎∴VABCDEF＝2VA－BEFD＝S四边形BEFD·OA＝2.‎ ‎5．[2017·全国卷Ⅲ]如图，四面体ABCD中，△ABC是正三角形，AD＝CD.‎ ‎(1)证明：AC⊥BD；‎ ‎(2)已知△ACD是直角三角形，AB＝BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．‎ 解　(1)证明：如图，取AC的中点O，连接DO，BO.‎ 因为AD＝CD，‎ 所以AC⊥DO.‎ 又由于△ABC是正三角形，‎ 所以AC⊥BO.‎ 从而AC⊥平面DOB，又BD⊂平面DOB，‎ 故AC⊥BD.‎ ‎(2)连接EO.‎ 由(1)及题设知∠ADC＝90°，所以DO＝AO.‎ 在Rt△AOB中，BO2＋AO2＝AB2.‎ 又AB＝BD，所以BO2＋DO2＝BO2＋AO2＝AB2＝BD2，故∠DOB＝90°.‎ 由题设知△AEC为直角三角形，所以EO＝AC.‎ 又△ABC是正三角形，且AB＝BD，所以EO＝BD.‎ 故E为BD的中点，从而E到平面ABC的距离为D到平面ABC的距离的，四面体ABCE的体积为四面体ABCD的体积的，即四面体ABCE与四面体ACDE的体积之比为1∶1.‎