【数学】2019届一轮复习北师大版解密函数零点相关问题学案

【数学】2019届一轮复习北师大版解密函数零点相关问题学案

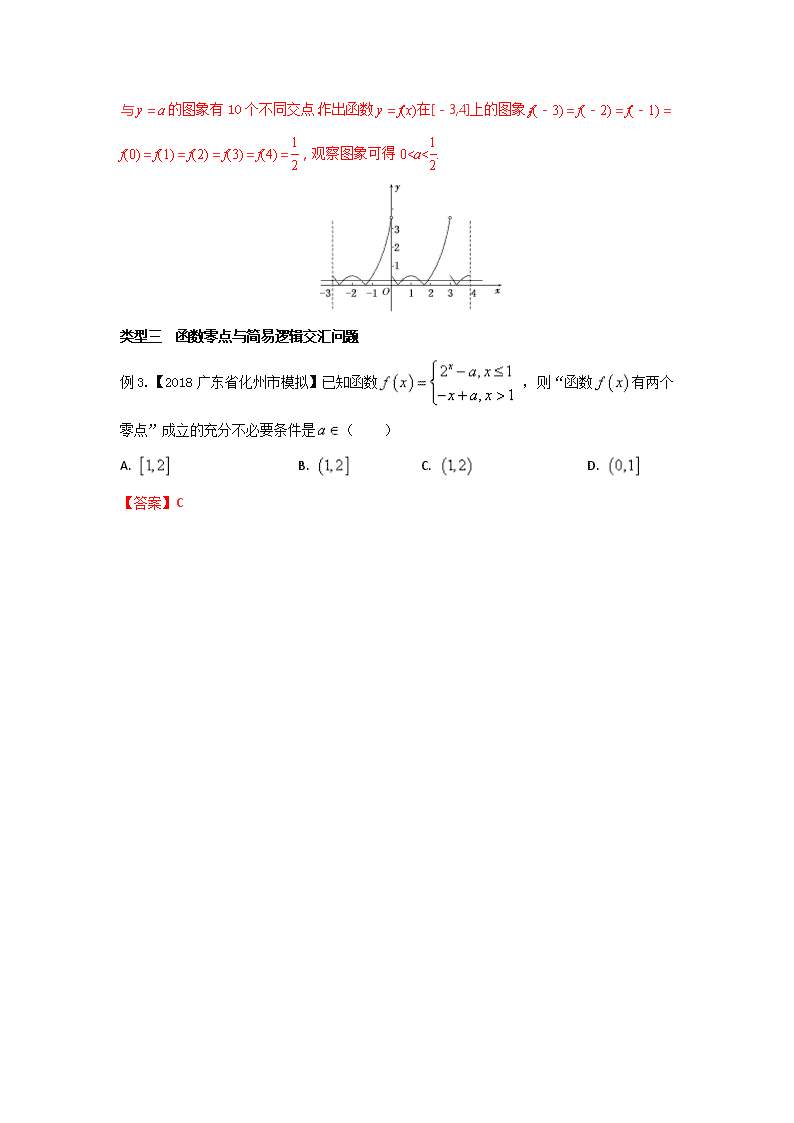
一．方法综述 新课标下的高考越 越注重对学生的综合素质的考察，函数的零点问题便是一个考察学生综合素质的很好途径，它主要涉及到基本初等函数的图象，渗透着转化、化归、数形结合、函数与方程等思想方法，在培养思维的灵活性、创造性等方面起到了积极的作用。近几年的数学高考中频频出现零点问题，其形式逐渐多样化，但都与函数、导数知识密不可分.‎ 根据函数零点的定义 对于函数，把使成立的实数叫做函数的零点。即 方程有实数根函数的图象与轴有交点的横坐标函数有零点。围绕三者之间的关系，在高考数学中函数零点的题型主要①函数的零点的分布；②函数的零点的个数问题；③利用导数结合图像的变动将两个函数的图像的交点问题转化成函数的零点的个数问题.‎ 二．解题策略 类型一 函数零点的分布问题 例1、(2014·北京高考)已知函数f(x)＝－log2x，在下列区间中，包含 f(x)零点的区间是(　　)‎ A．(0,1) B．(1,2) C．(2,4) D．(4，＋∞)‎ ‎【答案】C ‎【举一反三】函数f(x)＝ln ＋x－，则函数的零点所在区间是(　　)‎ A. B. C. D．(1，2)‎ ‎【答案】C ‎【解析】函数f(x)＝ln ＋x－的图象在(0，＋∞)上连续，且＝ln＋－＝ln ‎＋＜0，f(1)＝ln 1＋1－＝＞0，故f(x)的零点所在区间为. ‎ 类型二 函数零点的个数问题 ‎【例2】【2017课标3】已知函数有唯一零点，则（ ） ‎ A． B． C． D．1‎ ‎【答案】C ‎【举一反三】已知f(x)是定义在R上且周期为3的函数，当x∈[0,3)时，f(x)＝.若函数y＝f(x)－a在区间[－3,4]上有10个零点(互不相同)，则实数a的取值范围是________．‎ ‎【答案】‎ ‎【解析】函数y＝f(x)－a在区间[－3,4]上有互不相同的10个零点，即函数y＝f(x)，x∈[－3,4]与y＝a的图象有10个不同交点．作出函数y＝f(x)在[－3,4]上的图象，f(－3)＝f(－2)＝f(－1)＝f(0)＝f(1)＝f(2)＝f(3)＝f(4)＝，观察图象可得01；对命题q，令2－a<0，即a>2，则q对应的a的取值范围是a≤2.∵p∧(q)为真命题，‎ ‎∴实数a的取值范围是(1，2]． ‎ 三．强化训练 ‎1．设定义域为(0，＋∞)的单调函数f(x)对任意的x∈(0，＋∞)，都有f[f(x)－log2x]＝3，若x0是方程f(x)－f′(x)＝2的一个解，则x0存在的区间是(　　)‎ A．(0,1) B．(1,2) C．(2,3) D．(3,4)‎ ‎【答案】C ‎ 2.【2017湖北省荆州市质检】已知函数，用表示中最小值，设，则函数的零点个数为( )‎ A．1 B．2 C. 3 D．4‎ ‎【答案】C ‎【解析】作出函数和的图象如图，两个图象的下面部分图象，由，得，或，由，得或， ‎ ‎∵，∴当时，函数的零点个数为个，故选 C．‎ ‎3.【2018广西壮族自治区贺州市桂梧高中联考】已知表示不大于的最大整数，若函数在上仅有一个零点，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎4.【2018四川省广元市统考】函数，若关于的方程有五个不同的零点，则的取值范围（ ） ‎ A. （1，2） B. C. D. ‎ ‎【答案】D ‎ 5.【2018广西贺州桂梧联考】已知表示不大于的最大整数，若函数在上仅有一个零点，则的取值范围为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】若，当， ， .，∴当，即时， 在上有一个零点. ‎ 当， ， ， ， ，故在 上无零点.[ ‎ 若，当， 在上无零点.当， ， .∴当，即（此时对称轴）时， 在上有一个零点.故当时， 在上仅有一个零点.选D ‎6.【2018内蒙古呼和浩特市研】已知函数，若存在唯一的正整数，使得，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎ 所以的取值范围是 故选C ‎7.已知函数，若对任意的，在区间总存在唯一的零点，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎ 8.【2018四川省绵阳市一诊】已知是函数的零点，是函数的零点，且满足，则实数的最小值是（　　）‎ A. B. C. D.‎ ‎【答案】D ‎【解析】因为，所以当时， 单调递减，当时， 单调递增， ，即函数存在唯一零点，即， 因为，所以，即在有零点，（1）若，即，此时的零点为，显然符合题意；（2）若，即或，若在[﹣2，0]上只有一个零点，则， ，②若在[﹣2，0]上有两个零点，则 ‎，解得，即的最小值为；故选D.‎ ‎9.【2018山东省德州市预测】已知f（x）=ax2+（b-a）x+c-b（其中a＞b＞c），若a+b+c=0，x1、x2为f（x）的两个零点，则|x1-x2|的取值范围为 .‎ ‎【答案】‎ ‎ 10.【2017年第一次全国大联考（新课标卷Ⅰ）】已知函数的零点为,的零点为,若,则实数a的取值范围是 .‎ ‎【答案】‎ ‎【解析】由可得,令,得.当时,单调递增;当时,单调递减,故,故.由可得,由,得,所以是增函数,则,解得.‎ ‎11.【2017山东潍坊联考】设函数，若函数有三个零点，，，则等于 . ‎ ‎【答案】‎ ‎ 12.已知函数在上有两个不同的零点，记，则的取值范围为______．‎ ‎【答案】‎ ‎【解析】由题意，得，即．设，当时，，此时如图所示的平面区域的阴影部分，易知．‎