高中数学必修1知识点及题型
1.集合
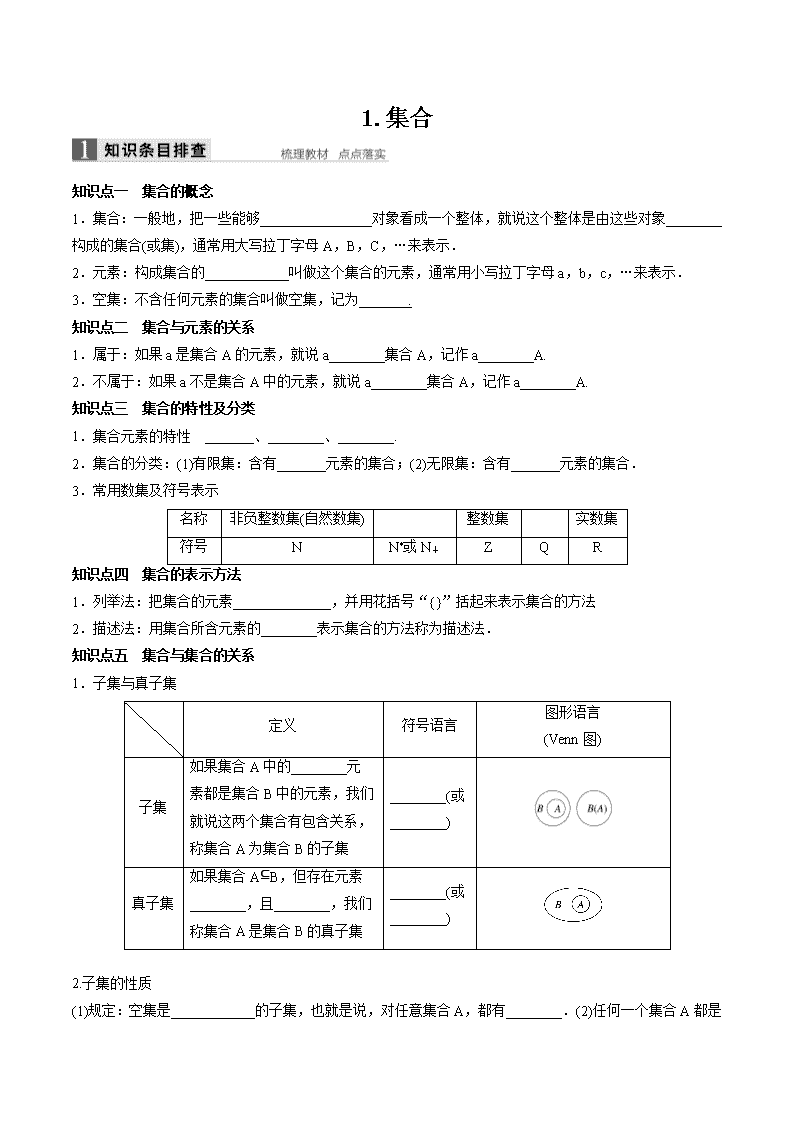
知识点一 集合的概念
1.集合:一般地,把一些能够________________对象看成一个整体,就说这个整体是由这些对象________
构成的集合(或集),通常用大写拉丁字母 A,B,C,…来表示.
2.元素:构成集合的____________叫做这个集合的元素,通常用小写拉丁字母 a,b,c,…来表示.
3.空集:不含任何元素的集合叫做空集,记为 .
知识点二 集合与元素的关系
1.属于:如果 a 是集合 A 的元素,就说 a________集合 A,记作 a________A.
2.不属于:如果 a 不是集合 A 中的元素,就说 a________集合 A,记作 a________A.
知识点三 集合的特性及分类
1.集合元素的特性 _______、________、________.
2.集合的分类:(1)有限集:含有_______元素的集合;(2)无限集:含有_______元素的集合.
3.常用数集及符号表示
名称 非负整数集(自然数集) 整数集 实数集
符号 N N*或 N+ Z Q R
知识点四 集合的表示方法
1.列举法:把集合的元素______________,并用花括号“{}”括起来表示集合的方法
2.描述法:用集合所含元素的________表示集合的方法称为描述法.
知识点五 集合与集合的关系
1.子集与真子集
定义 符号语言
图形语言
(Venn 图)
子集
如果集合 A 中的________元素
都是集合 B 中的元素,我们就
说这两个集合有包含关系,称
集合 A 为集合 B 的子集
________(或
________)
真子集
如果集合 A⊆B,但存在元素
________,且________,我们
称集合 A 是集合 B 的真子集
________(或
________)
2.子集的性质
(1)规定:空集是____________的子集,也就是说,对任意集合 A,都有________.(2)任何一个集合 A 都是
它本身的子集,即________.(3)如果 A⊆B,B⊆C,则________.(4)如果 A B,B C,则________.
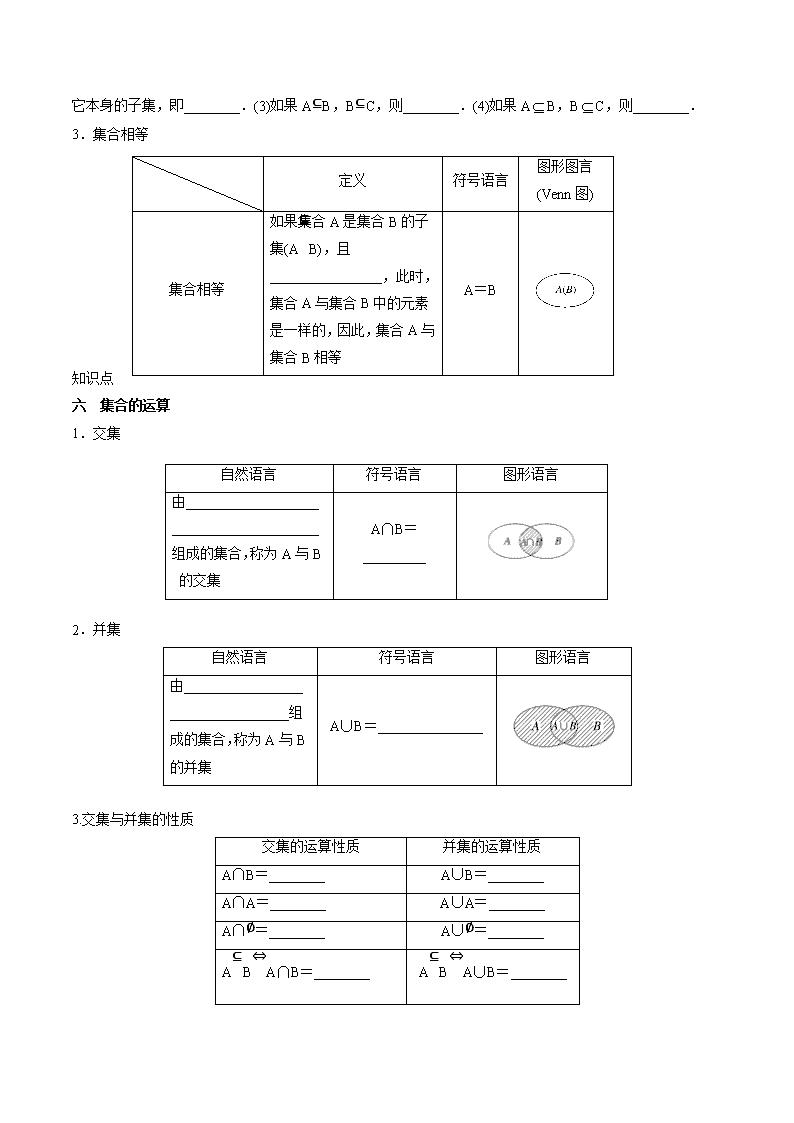
3.集合相等
知识点
六 集合的运算
1.交集
2.并集
自然语言 符号语言 图形语言
由_________________
_________________组
成的集合,称为 A 与 B
的并集
A∪B=_______________
3.交集与并集的性质
交集的运算性质 并集的运算性质
A∩B=________ A∪B=________
A∩A=________ A∪A=________
A∩∅ =________ A∪∅ =________
A⊆B⇔A∩B=________ A⊆B⇔A∪B=________
定义 符号语言
图形图言
(Venn 图)
集合相等
如果集合 A 是集合 B 的子
集(A⊆B),且
________________,此时,
集合 A 与集合 B 中的元素
是一样的,因此,集合 A 与
集合 B 相等
A=B
自然语言 符号语言 图形语言
由___________________
_____________________
组成的集合,称为 A 与 B
的交集
A∩B=
_________
4.全集
在研究集合与集合之间的关系时,如果一个集合含有我们所研究问题中涉及的________,那么就称这个集
合为全集,通常记作________.
5.补集
文字语言
对于一个集合 A,由全集 U 中__________的所有元素组成的集
合称为集合 A 相对于全集 U 的补集,记作________
符号语言 ∁ UA=________________
图形语言
典例精讲
题型一 * 判断能否构成集合
1.在“①高一数学中的难题;②所有的正三角形;③方程 x2-2=0 的实数解”中,能够构成集合的是 。
题型二 * 验证元素是否是集合的元素
1、已知集合 ZnZmnmxxA ,,22 ,判断 3 是不是集合 A 的元素。
2、集合 A 是由形如 ZnZmnm ,3 的数构成的,判断
32
1
是不是集合 A 中的元素.
题型三 ** 求集合
1.方程组 3x+y=2
2x-3y=27
的解集是( )
A.
x=3
y=-7
B.{x,y|x=3 且 y=-7} C.{3,-7} D.{(x,y)|x=3 且 y=-7}
2.下列六种表示法:①{x=-1,y=2};②{(x,y)|x=-1,y=2};③{-1,2};④(-1,2);⑤{(-1,2)};
⑥{(x,y)|x=-1 或 y=2}.
能表示方程组 2x+y=0,
x-y+3=0
的解集的是( )
A.①②③④⑤⑥ B.②③④⑤ C.②⑤ D.②⑤⑥
题型四 ** 利用集合中元素的性质求参数
1.已知集合 S={a,b,c}中的三个元素是△ABC 的三边长,那么△ABC 一定不是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
2.设 a,b∈R,集合{1,a+b,a}= 0,b
a
,b ,则 b-a=________.
3.已知 P={x|2<x<k,x∈N,k∈R},若集合 P 中恰有 3 个元素,则实数 k 的取值范围是________.
4.已知集合 A 是由 0,m,m2-3m+2 三个元素组成的集合,且 2∈A,则实数 m 的值为( )
A.2 B.3 C.0 或 3 D.0 或 2 或 3
题型五 ** 判断集合间的关系
1、设
ZkkxxM ,4
1
2 ,
ZkkxxN ,2
1
4
,则 M 与 N 的关系正确的是( )
A. M=N B. NM
C. NM
D.以上都不对
2.判断下列集合间的关系:
(1)A={x|x-3>2},B={x|2x-5≥0};
(2)A={x∈Z|-1≤x<3},B={x|x=|y|,y∈A}.
题型六 ** 求子集个数
1.已知集合 A={x|ax2+2x+a=0,a∈R},若集合 A 有且仅有 2 个子集,则 a 的取值构成的集合为________.
2.已知集合 A={1,2,3},写出集合 A 的所有子集,非空子集,真子集,非空真子集
题型七 ** 利用两个集合之间的关系求参数
1.已知集合 A={1,2,m3},B={1,m},B⊆A,则 m=________.
2.已知集合 A={1,2},B={x|ax-2=0},若 B⊆A,则 a 的值不可能是( )
A.0 B.1 C.2 D.3
题型八 *** 集合间的基本运算
1.下面四个结论:①若 a∈(A∪B),则 a∈A;②若 a∈(A∩B),则 a∈(A∪B);③若 a∈A,且 a∈B,
则 a∈(A∩B);④若 A∪B=A,则 A∩B=B.其中正确的个数为( )
A.1 B.2 C.3 D.4
2.已知集合 M={x|-3
3},则 M∪N=( )
A.{x|x>-3} B.{x|-30},则 S∩T=( )
A.[2,3] B.(-∞,2]∪[3,+∞) C.[3,+∞) D.(0,2]∪[3,+∞)
5.下列关系式中,正确的个数为( )
①(M∩N)⊆N;②(M∩N)⊆(M∪N);③(M∪N)⊆N;④若 M⊆N,则 M∩N=M.
A.4 B.3 C.2 D.1
6.(2016·唐山一中月考试题)已知全集 U={x|x≤4},集合 A={x|-2a} {x|x≤a} {x|xf(x2),那么就说函数 f(x)在区间 D 上是减函数.
2.函数的单调性:若函数 f(x)在区间 D 上是增(减)函数,则称函数 f(x)在这一区间上具有(严格的)单调
性,区间 D 叫做 f(x)的单调区间.
3.单调性的常见结论:若函数 f(x),g(x)均为增(减)函数,则 f(x)+g(x)仍为增(减)函数;若函数 f(x)为
增(减)函数,则-f(x)为减(增)函数;若函数 f(x)为增(减)函数,且 f(x)>0,则 1
fx
为减(增)函数.
知识点八 函数的最大值、最小值
最值
类别
最大值 最小值
条件
设函数 y=f(x)的定义域为 I,如果存在实数 M 满足
(1)对于任意的 x∈I,都有
__________
(2)存在 x0∈I,使得______________
(1)对于任意的 x∈I,都有________
(2)存在 x0∈I,使得________
结论 M 是函数 y=f(x)的最大值 M 是函数 y=f(x)的最小值
性质:定义在闭区间上的单调函数,必有最大(小)值.
知识点九 函数的奇偶性
1.函数奇偶性的概念
偶函数 奇函数
条件
对于函数 f(x)的定义域内任意一个 x,都有
f(-x)=f(x) f(-x)=-f(x)
结论 函数 f(x)是偶函数 函数 f(x)是奇函数
2.性质
(1)偶函数的图象关于 y 轴对称;奇函数的图象关于原点对称,奇函数在原点有定义,则 f(x)=0
(2)奇函数在对称的区间上单调性相同,偶函数在对称的区间上单调性相反.
(3)在定义域的公共部分内,两个奇函数之积与商(分母不零)为偶函数;两个奇函数之和为奇函数;两
个偶函数的和、积与商为偶函数;一奇一偶函数之积与商(分母不为零)为奇函数.
知识点十 函数的周期性
若存在非零常数 T,对定义域内任意 x,都有 ( )f x T f x ,称这样的函数为周期函数,T
叫函数的一个周期。
如:若 ,则f x a f x ( )
典例精讲
题型一 *** 函数的定义域
1 函数 f(x)=ln(x-3)的定义域为( )
A.{x|x>-3} B.{x|x>0} C.{x|x>3} D.{x|x≥3}
2.函数 f(x)= 1-2x+ 1
x+3
的定义域为( )
A.(-3,0] B.(-3,1] C.(-∞,-3)∪(-3,0] D.(-∞,-3)∪(-3,1]
3.函数
2 3 4x xy x
的定义域为( )
A.[ 4,1] B.[ 4, 0) C.(0,1] D.[ 4, 0) (0,1]
4.已知函数 f(x)= 12 mxmx 的定义域是一切实数,则 m 的取值范围是( )
A.00, f(x)=x2+x,求 f(x)解析式
3、设 )(xf 是奇函数, )(xg 是偶函数,并且 xxxgxf 2)()( ,求 )(xf 。
题型六 ** 函数的值域与最值
1、函数 2 2 3y x x , 4,1x 的值域为 .
2、求函数
5
1)(
x
xxf 4,1x 的最大值和最小值。
3、求函数 324)( 1 xxxf 4,2x 的最大值和最小值。
题型七 *** 函数性质的考察
1、写出函数 )34(log)( 2
2
1 xxxf 的单调递减区间
2、设二次函数 f(x)=x2-(2a+1)x+3
(1)若函数 f(x)的单调增区间为 ,2 ,则实数 a 的值__________;
(2)若函数 f(x)在区间 ,2 内是增函数,则实数 a 的范围__________。
3、定义在 )1,1( 上的奇函数
1
)( 2
nxx
mxxf ,则常数 m ____, n _____
4、已知函数 ( )f x 是 ( , ) 上的偶函数,若对于 0x ,都有 ( 2 ( )f x f x ) ,且当 [0,2)x 时,
2( ) log ( 1f x x ),则 ( 2008) (2009)f f 的值为( )
A. 2 B. 1 C.1 D. 2
5、函数 2
2log 2
xy x
的图像 ( )
A.关于原点对称 B.关于主线 y x 对称 C .关于 y 轴对称 D.关于直线 y x 对称
6、函数 4 1
2
x
xf x 的图象( )
A. 关于原点对称 B. 关于直线 y=x 对称 C. 关于 x 轴对称 D. 关于 y 轴对称
7、定义在 R 上的奇函数 )(xf ,满足 ( 4) ( )f x f x ,且在区间[0,2]上是增函数,则 ()
A. ( 25) (11) (80)f f f B. (80) (11) ( 25)f f f
C. (11) (80) ( 25)f f f D. ( 25) (80) (11)f f f
8、已知偶函数 ( )f x 在区间0, ) 单调增加,则满足 (2 1)f x < 1( )3f 的 x 取值范围( )
(A)( 1
3
, 2
3
) B.[ 1
3
, 2
3
) C.( 1
2
, 2
3
) D.[ 1
2
, 2
3
)
9、定义在 R 上的偶函数 ( )f x 满足:对任意的 1 2 1 2, [0, )( )x x x x ,有 2 1
2 1
( ) ( ) 0f x f x
x x
.则 ( )
(A) (3) ( 2) (1)f f f B. (1) ( 2) (3)f f f
C. ( 2) (1) (3)f f f D. (3) (1) ( 2)f f f
10 、 已 知 函 数 ( )f x 是 定 义 在 实 数 集 R 上 的 不 恒 为 零 的 偶 函 数 , 且 对 任 意 实 数 x 都 有
( 1) (1 ) ( )xf x x f x ,则 5( ( ))2f f 的值是 ( )
A.0 B. 1
2
C.1 D. 5
2
11、已知定义在 R 上的奇函数 )(xf ,满足 ( 4) ( )f x f x ,且在区间[0,2]上是增函数,若方程
f(x)=m(m>0)在区间 8,8 上有四个不同的根 1 2 3 4, , ,x x x x ,则 1 2 3 4 _________.x x x x
12、已知函数 f(x)=1+ax2
x+b
的图象经过点(1,3),并且 g(x)=xf(x)是偶函数.
(1)求函数中 a、b 的值;
(2)判断函数 g(x)在区间(1,+∞)上的单调性,并用单调性定义证明.
基本初等函数、方程的根与函数的零点
知识点一 指数函数
(1)根式的概念:
(2)如果 , , , 1nx a a R x R n ,且 n N ,那么 x 叫做 a 的 n 次方根.
(3)分数指数幂的概念:
(4)①正数的正分数指数幂的意义是: ( 0, , ,
m
n mna a a m n N 且 1)n .0 的正分数指数幂等于 0.
(5)②正数的负分数指数幂的意义是:
1 1( ) ( ) ( 0, , ,
m m
mn n na a m n Na a
且 1)n .0 的负分数指数
幂没有意义.
(6)运算性质:
① ( 0, , )r s r sa a a a r s R ②( ) ( 0, , )r s rsa a a r s R
③( ) ( 0, 0, )r r rab a b a b r R
(7)指数函数
知识点二 对数函数
(1)对数的定义:
①若 ( 0, 1)xa N a a 且 ,则 x 叫做以 a 为底 N 的对数,记作 logax N ,其中 a 叫做底数, N 叫
做真数.
②负数和零没有对数.
③对数式与指数式的互化: log ( 0, 1, 0)x
ax N a N a a N .
(2)几个重要的对数恒等式:log 1 0a ,log 1a a ,log b
a a b .
函数名称 指数函数
定义 函数 ( 0xy a a 且 1)a 叫做指数函数
图象
1a 0 1a
定义域 R
值域 (0, )
过定点 图象过定点(0,1) ,即当 0x 时, 1y .
奇偶性 非奇非偶
单调性 在 R 上是增函数 在 R 上是减函数
函数值的
变化情况
1 ( 0)
1 ( 0)
1 ( 0)
x
x
x
a x
a x
a x
1 ( 0)
1 ( 0)
1 ( 0)
x
x
x
a x
a x
a x
a 变化对图象
的影响 在第一象限内,a 越大图象越高;在第二象限内, a 越大图象越低.
O
A 0
1
xay
x
y
(0,1)
O
1y
(3)常用对数与自然对数
常用对数:lg N ,即 10log N ;自然对数:ln N ,即loge N (其中 2.71828e …).
(4)对数的运算性质 如果 0, 1, 0, 0a a M N ,那么
①加法:log log log ( )a a aM N MN ②减法:log log loga a a
MM N N
③数乘: log log ( )n
a an M M n R ④ loga Na N
5 log log ( 0, )b
n
aa
nM M b n Rb
⑥换底公式: loglog ( 0, 1)log
b
a
b
NN b ba
且
(5)对数函数
函数
名称 对数函数
定义 函数 log ( 0ay x a 且 1)a 叫做对数函数
图象
1a 0 1a
定义域 (0, )
值域 R
过定点 图象过定点(1,0) ,即当 1x 时, 0y .
奇偶性 非奇非偶
单调性 在(0, ) 上是增函数 在(0, ) 上是减函数
函数值的
变化情况
log 0 ( 1)
log 0 ( 1)
log 0 (0 1)
a
a
a
x x
x x
x x
log 0 ( 1)
log 0 ( 1)
log 0 (0 1)
a
a
a
x x
x x
x x
a 变化对函数图象的
影响 在第一象限内,a 越大图象越靠低;在第四象限内,a 越大图象越靠高.
1
1
x
y
O
(1,0)
1x
logay x
1
1
x
y
O (1,0)
1x
logay x
知识点三 幂函数
(1)幂函数的定义
一般地,函数 y x 叫做幂函数,其中 x 为自变量, 是常数.
(2)幂函数的图象过定点:所有的幂函数在(0, ) 都有定义,并且图象都通过点(1,1) .
知识点四 函数与方程
1、函数零点的定义
(1)对于函数 )(xfy ,我们把方程 0)( xf 的实数根叫做函数 )(xfy 的零点。
(2)方程 0)( xf 有实根 函数 ( )y f x 的图像与 x 轴有交点 函数 ( )y f x 有零点。因此判断一
个函数是否有零点,有几个零点,就是判断方程 0)( xf 是否有实数根,有几个实数根。函数零点的求
法:解方程 0)( xf ,所得实数根就是 ( )f x 的零点
(3)变号零点与不变号零点
①若函数 ( )f x 在零点 0x 左右两侧的函数值异号,则称该零点为函数 ( )f x 的变号零点。
②若函数 ( )f x 在零点 0x 左右两侧的函数值同号,则称该零点为函数 ( )f x 的不变号零点。
③若函数 ( )f x 在区间 ,a b 上的图像是一条连续的曲线,则 0)()( bfaf 是 ( )f x 在区间 ,a b 内有零点的充
分不必要条件。
2、函数零点的判定
(1)零点存在性定理:如果函数 )(xfy 在区间 ],[ ba 上的图象是连续不断的曲线,并且有 ( ) ( ) 0f a f b ,
那么,函数 )(xfy 在区间 ,a b 内有零点,即存在 ),(0 bax ,使得 0)( 0 xf ,这个 0x 也就是方程 0)( xf
的根。
(2)函数 )(xfy 零点个数(或方程 0)( xf 实数根的个数)确定方法
① 代数法:函数 )(xfy 的零点 0)( xf 的根;
②(几何法)对于不能用求根公式的方程,可以将它与函数 )(xfy 的图象联系起来,并利用函数的
性质找出零点。
(3)零点个数确定
0 )(xfy 有 2 个零点 0)( xf 有两个不等实根;
0 )(xfy 有 1 个零点 0)( xf 有两个相等实根;
0 )(xfy 无零点 0)( xf 无实根;对于二次函数在区间 ,a b 上的零点个数,要结合图像进
行确定.
1、二分法
(1)二分法的定义:对于在区间[ , ]a b 上连续不断且 ( ) ( ) 0f a f b 的函数 ( )y f x ,通过不断地把函数
( )y f x 的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点的近似值的方法
叫做二分法;
(2)用二分法求方程的近似解的步骤:
① 确定区间[ , ]a b ,验证 ( ) ( ) 0f a f b ,给定精确度 ;
②求区间 ( , )a b 的中点c ;
③计算 ( )f c ;
(ⅰ)若 ( ) 0f c ,则c 就是函数的零点;
(ⅱ) 若 ( ) ( ) 0f a f c ,则令b c (此时零点 0 ( , )x a c );
(ⅲ) 若 ( ) ( ) 0f c f b ,则令 a c (此时零点 0 ( , )x c b );
④判断是否达到精确度 ,即 a b ,则得到零点近似值为 a (或b );否则重复②至④步.
典例精讲
题型一 ** 有关幂函数定义及性质
1、函数 2 2( 1) my m x 是一个反比例函数,则 m= .
2、在函数①y=x3 ②y=x2 ③y=x-1 ④y= x 中,定义域和值域相同的是 .
3、将 2
1
2.1a , 2
1
9.0
b , 2
1
1.1c 按从小到大进行排列为________
题型二 *** 指数函数及其性质
1、函数 0.(12 aay x 且 )1a 的图像必经过点
2、 比较下列各组数值的大小:
(1) 3.37.1 1.28.0 ; (2) 7.03.3 8.04.3 ;
3、函数
2 21
2
x x
y
的递减区间为 ;值域是
4、设 20 x ,求函数
1
24 3 2 5
x xy
的最大值和最小值。
5、设 dcba ,,, 都是不等于1的正数, xxxx dycybyay ,,, 在同一坐标系中的图像如图所示,
则 dcba ,,, 的大小顺序是
A.a b c d B.a b d c C.b a d c D.b a c d
题型三 ** 指数函数的运算
1、计算
1
2 2( 2) 的结果是()
A、 2 B、 1
2
C、— 2 D、— 1
2
2、
4 4
3 66 39 9a a 等于()
A、 16a B、 8a C、 4a D、 2a
3、若 53,83 ba ,则 ba 233
= 。
题型四 ** 对数运算
1、求值 2 2 3 3(log 3 2log 3)(3log 4 log 2) ;
2、已知3 2a ,那么 3 3log 8 2log 6 用 a 表示是()
A、 2a B、5 2a C、
23 (1 )a a D、 23a a
3、已知 7 3 2log [log (log )] 0x ,那么
1
2x
等于()
A、 1
3
B、 1
2 3
C、 1
2 2
D、 1
3 3
题型五 *** 对数函数及其性质
1、指数函数 xy a ( 0a 且 )1a 的反函数为 ;它的值域是
2、已知 1 1
2 2
log log 0m n ,则 ( )
.A 1n m .B 1m n .C 1 m n .D 1 n m
3、 3
2
)2.1(a , 3
2
1.1b ,
1
30.9c , 3log 0.34d 的大小关系是
4、已知
2
1log a <0 ,( a >0, a ≠1),则 a 的取值范围是 .
5、函数 ( ) log (2 1)af x x ( a >0,且 a ≠1)的图像必经过点
6、已知 y=loga(2-ax)在[0,1]上是关于 x 的减函数,则 a 的取值范围是 ( )
A.(0,1) B.(1,2) C.(0,2) D. ),2[
题型六 *** 零点区间的判断
1、函数 f(x)=2x+3x 的零点所在的一个区间是( )
A、(-2,-1) B、(-1,0) C、(0,1) D、(1,2)
2、函数 f(x)=log2x+2x-1 的零点必落在区间 ( )
A、
4
1,8
1 B、
2
1,4
1 C、
1,2
1 D、(1,2)
3、设 2( ) 3xf x x ,则在下列区间中,使函数 )(xf 有零点的区间是( )
A、[0,1] B、[1,2]
4、在下列区间中,函数 ( ) e 4 3xf x x 的零点所在的区间为 ( )
A、 1( ,0)4
B、 1(0, )4
C、 1 1( , )4 2
D、 1 3( , )2 4
5、若 0x 是方程 lg 2x x 的解,则 0x 属于区间 ( )
A、(0,1) B、(1,1.25) C、(1.25,1.75) D、(1.75,2)
题型七 *** 零点个数的判断
1、方程 22 3x x 的实数解的个数为 .
2、函数 ( ) ln 2f x x x 的零点个数为 .
3、函数 2( ) cosf x x x 在区间[0,4]上的零点个数为 ( )
A、4 B、5 C、6 D、7
4、函数 ( ) cosf x x x 在[0, ) 内 ( )
A、没有零点 B、有且仅有一个零点
C、有且仅有两个零点 D、有无穷多个零点
5、函数
2 2 3, 0( )
2 ln , 0
x x xf x
x x
, 零点个数为 ( )
A、3 B、2 C、1 D、0
6、若函数 )(xf xa x a ( 0a 且 1a )有两个零点,则实数 a 的取值范围是 .
7、若函数 3( ) 3f x x x a 有 3 个不同的零点,则实数 a 的取值范围是( )
A、 2,2 B、 2,2 C、 , 1 D、 1,
题型八 ** 二分法求函数零点
1、下列函数中能用二分法求零点的是 ( )
2、下列函数图象与 x 轴均有交点,但不宜用二分法求交点横坐标的是 ( )
3 、 设 833 xxf x , 用 二 分 法 求 方 程 2,10833 xxx 在 内 近 似 解 的 过 程 中 得
,025.1,05.1,01 fff 则方程的根落在区( )
A、(1,1.25) B、(1.25,1.5) C、(1.5,2) D、不能确定
4、用二分法研究函数 13)( 3 xxxf 的零点时,第一次经计算 0)5.0(0)0( ff , ,可得其中一个零点
0x ,第二次应计算 . 以上横线上应填的内容为 ( )
A、(0,0.5), )25.0(f B、(0,1), )25.0(f
C、(0.5,1), )75.0(f D、(0,0.5), )125.0(f
5、若函数 3 2( ) 2 2f x x x x 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
f (1) = -2 f (1.5) = 0.625 f (1.25) = -0.984
f (1.375) = -0.260 f (1.4375) = 0.162 f (1.40625) = -0.054
那么方程 3 2 2 2 0x x x 的一个近似根(精确到 0.1)为 ( )
A、1.2 B、1.3 C、1.4 D、1.5