- 2021-06-16 发布 |
- 37.5 KB |
- 3页


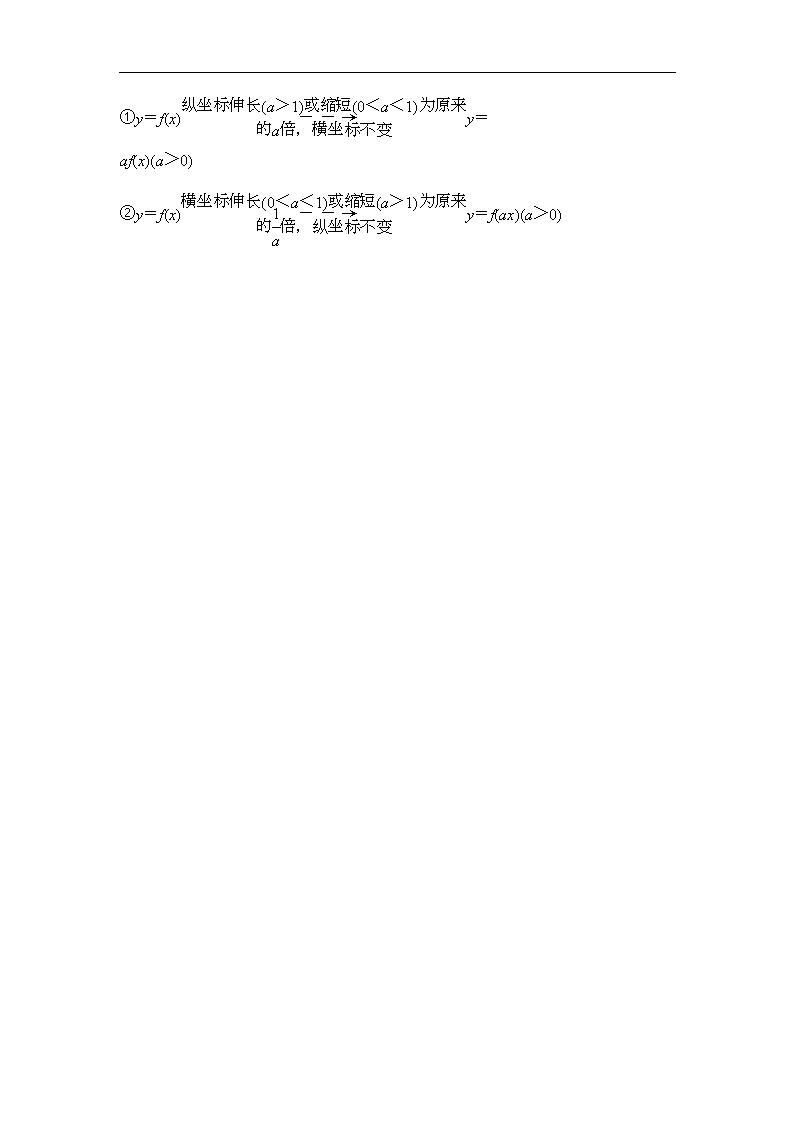
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习教案: 函数的图象
函数的图象 主标题:函数的图象 副标题:为学生详细的分析函数的图象的高考考点、命题方向以及规律总结。 关键词:图象,变换,图象应用 难度:4 重要程度:5 考点剖析: 1.在实际情境中,会根据不同的需要选择图象法、列表法、解析法表示函数. 2.会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式的解的问题. 命题方向:常考查:①由函数的性质(如单调性、对称性、最值)及图象的变换选图象;②在解方程或不等式问题时,利用图象求交点个数或解集的范围,是高考考查的热点,常以选择题形式考查,难度中档. 规律总结:1.掌握平移变换、伸缩变换、对称变换、翻折变换、周期变换等常用的方法技巧,来帮助我们简化作图过程. 2.识图的要点:重点根据图象看函数的定义域、值域、奇偶性、单调性、特殊点(与x、y轴的交点,最高、最低点等). 3.识图的方法 (1)定性分析法:对函数进行定性分析,从而得出图象的上升(或下降)的趋势,利用这一特征分析解决; (2)定量计算法:通过定量的计算来分析解决; (3)排除法:利用本身的性能或特殊点进行排除验证. 4.研究函数性质时一般要借助于函数图象,体现了数形结合思想; 5.方程解的问题常转化为两熟悉的函数图象的交点个数问题来解决. 知 识 梳 理 1.函数的图象及作法 2.图象变换 (1)平移变换 (2)对称变换 ①y=f(x)y=-f(x); ②y=f(x)y=f(-x); ③y=f(x)y=-f(-x); ④y=ax(a>0且a≠1)y=logax(a>0且a≠1). (3)翻折变换 ①y=f(x)y=|f(x)|. ②y=f(x)y=f(|x|). (4)伸缩变换 ①y=f(x)y= af(x)(a>0) ②y=f(x)y=f(ax)(a>0)查看更多