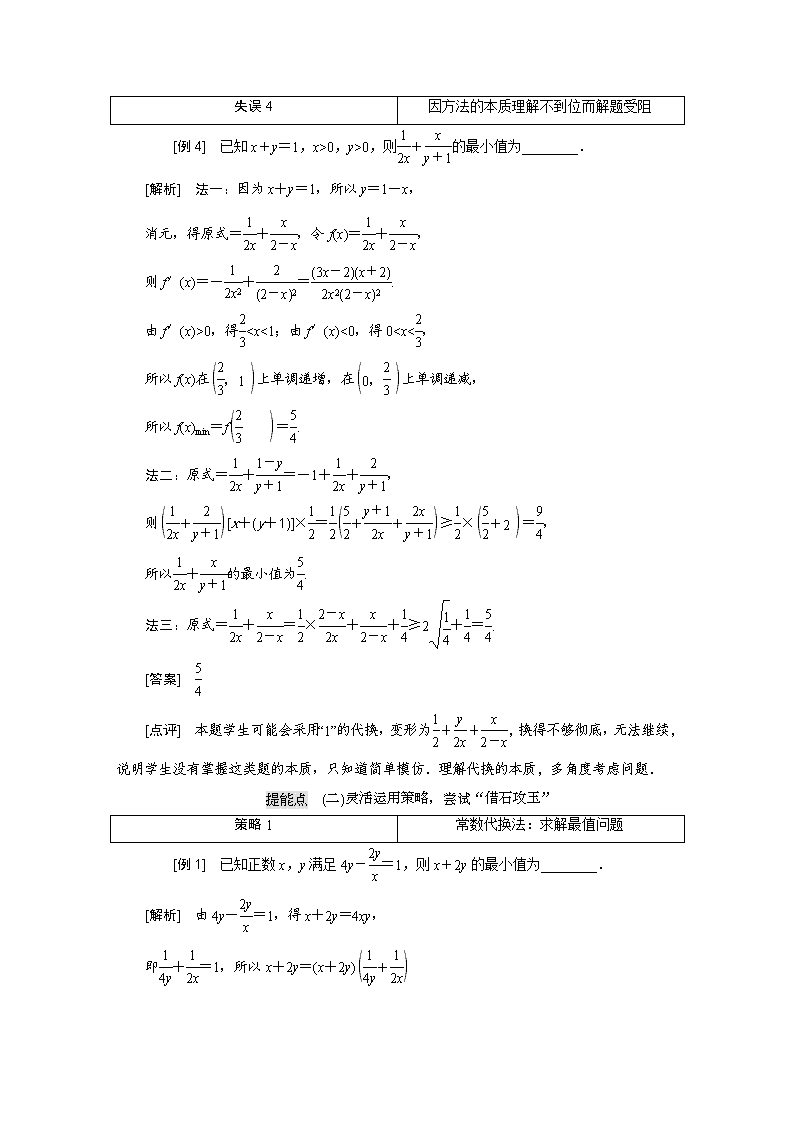【数学】2020届一轮复习苏教版专题五第五讲专题提能——“函数、不等式与导数”专题提能课学案
第五讲 专题提能——“函数、不等式与导数”专题提能课
失误1
因忽视二次项系数的讨论而失误
[例1] 不等式ax2+ax+1>0的解集为R,则实数a的取值范围是________.
[解析] 当a=0时,满足题意;当a≠0时,必有解得0
0,y>0,则+的最小值为________.
[解析] 法一:因为x+y=1,所以y=1-x,
消元,得原式=+,令f(x)=+,
则f′(x)=-+=.
由f′(x)>0,得4x+p-3成立的x的取值范围是________.
[解析] 设f(p)=(x-1)p+x2-4x+3,
则当x=1时,f(p)=0.所以x≠1.
f(p)在0≤p≤4上恒为正,等价于
即解得x>3或x<-1.
[答案] (-∞,-1)∪(3,+∞)
[点评] (1)本题若按常规法视x为主元来解,需要分类讨论,这样会很繁琐,若以p为主元,即将原问题化归为在区间[0,4]上,使一次函数f(p)=(x-1)p+x2-4x+3>0成立的参数x的取值范围,再借助一次函数的单调性就很容易使问题得以解决.
(2)在处理多变元的数学问题时,我们可以选取其中的常数(或参数),将其看做是“主元”,实现主与次的转化,即常量与变量的转化,从而达到减元的目的.
含参函数问题的处理方法
[典例] 设函数f(x)=-k(k为常数,e=2.718 28…是自然对数的底数).
(1)当k≤0时,求函数f(x)的单调区间;
(2)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
[解] (1)由函数f(x)=-k(x>0),可得f′(x)=.
当k≤0时,因为x>0,所以ex-kx>0.于是当02时,f′(x)>0.所以函数f(x)在(0,2)上为减函数,在(2,+∞)上为增函数.
(2)法一:由(1)知k≤0时,函数f(x)在(0,2)上单调递减,故f(x)在(0,2)上没有极值点.
当k>0时,设函数g(x)=ex-kx,x∈(0,+∞),则g′(x)=ex-k=ex-eln k.
当00,则g(x)单调递增,故f(x)在(0,2)上不存在两个极值点;
当k>1时,若x∈(0,ln k),则g′(x)=ex-k<0,则g(x)单调递减;若x∈(ln k,+∞),则g′(x)=ex-k>0,则g(x)单调递增.所以函数g(x)的最小值为g(ln k)=k(1-ln k),f(x)在(0,2)上存在两个极值点,当且仅当解得e0时,k>0,取对数得x=ln k+ln x.
令h(x)=x-ln x-ln k,x∈(0,+∞),
则h′(x)=1-=.
当x∈(0,1)时,h′(x)<0,h(x)单调递减;
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.
又因为当x→0时,h(x)→+∞.
所以函数f(x)在(0,2)内存在两个极值点,
当且仅当即
解得e0得x>1;由g′(x)<0得x<1.
所以函数g(x)在(0,1)上单调递减,在(1,2)上单调递增.
所以g(x)极小值=g(1)=e,又g(2)=,故k的取值范围为.
法四:由(1)知,当k≤0时,f(x)在(0,2)上单调递减,不存在极值点,所以k>0.
又f′(x)=,所以函数f(x)在(0,2)上存在两个极值点相当于h(x)=ex-kx在(0,2)上有两个变号零点(即零点左右函数值正负不同).
问题转化成函数y=k与g(x)=在(0,2)上有两个不同交点.
因为g′(x)=,x∈(0,2),
易求得g(x)在(0,1)上单调递减,在(1,2)上单调递增,且g(1)=e,g(2)=.
于是,结合函数图象,可得函数y=k与g(x)=在(0,2)上有两个不同交点的条件是k∈,即函数f(x)在(0,2)上存在两个极值点时,k的取值范围为.
法五:要使函数f(x)在区间(0,2)上存在两个极值点,
只需方程f′(x)=0在区间(0,2)上有两个不同的实根,
即=0⇔ex=kx在区间(0,2)内有两个不同的实根.
当x∈(0,2)时,由ex=kx得k=.
设g(x)=,x∈(0,2),则g′(x)=.
当x∈(0,1)时,g′(x)<0;当x∈(1,2)时,g′(x)>0.
于是函数g(x)在区间(0,1)上为减函数,在区间(1,2)上为增函数,
而当x→0时,g(x)→+∞;g(1)=e,
g(2)=.
结合函数g(x)的图象(如图①)可知:当k∈时,ex=kx在区间(0,2)上有两个不同的实根,即函数f(x)在区间(0,2)上存在两个极值点.
法六:函数f(x)在(0,2)上存在两个极值点,则f′(x)=0在(0,2)上有解.
f′(x)==0,即ex=kx.
当k≤0时,显然ex=kx不成立.
当k>0时,研究=在(0,2)上有解.
设g(x)=,g′(x)=.
当x∈(0,1)时,g′(x)>0;当x∈(1,2)时,g′(x)<0.
故函数g(x)在区间(0,1)上是增函数,在区间(1,2)上是减函数,
g(x)max=g(1)=,g(2)=,g(0)=0.
如图②所示,函数f(x)在(0,2)上存在两个极值点,则<<.
所以k的取值范围是.
[点评] 对于含参函数的处理,常用的方法有直接处理、参变分离、数形结合等方法,如何合理地转化(简化
)问题也是思考的重要方面,问题的不同表征方式会带来不同的思考途径和解题效果.
[课时达标训练]
A组——易错清零练
1.函数f(x)=的定义域为________________.
解析:由题意得
解得x>且x≠1,
故函数的定义域是.
答案:
2.y=的值域是________.
解析:令t=x-1,得x=t+1,
则y==t++1,
当t>0时,y=t++1≥2+1=3,
当且仅当t=1,即x=2时取等号.
同理:当t<0时,y=t++1=-+1≤-2+1=-1,
当且仅当t=-1,即x=0时取等号.
所以该函数的值域是(-∞,-1]∪[3,+∞).
答案:(-∞,-1]∪[3,+∞)
3.若函数f(x)=2x2-ln x在其定义域内的一个子区间(k-1,k+1)上不是单调函数,则实数k的取值范围是________.
解析:由题意,知函数的定义域为(0,+∞),f′(x)=4x-,由f′(x)=0,解得x=.
所以函数f(x)在上单调递减,在上单调递增.
故有解得1≤k<.
答案:
4.设f(x)是定义在R上的奇函数,且满足x>0时,f(x)+xf′(x)>0,f(2)=0,则不等式f(x)>0的解集为________.
解析:令F(x)=xf(x),则F′(x)=f(x)+xf′(x).
∵x>0时,f(x)+xf′(x)>0,
∴F(x)在(0,+∞)上单调递增.
∵f(x)是定义在R上的奇函数,
∴F(x)=xf(x)是定义在R上的偶函数.
∵f(2)=0,∴F(-2)=F(2)=2f(2)=0.
∴f(x)>0等价于或
解得x>2或-20).
①当a≤0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增,函数既无极大值,也无极小值;
②当a>0时,由f′(x)=0,得x=或x=-(舍去).
于是,当x变化时,f′(x)与f(x)的变化情况如下表:
x
(0,)
(,+∞)
f′(x)
-
0
+
f(x)
所以函数f(x)的单调递减区间是(0,),单调递增区间是(,+∞).
函数f(x)在x=处取得极小值f()=,无极大值.
综上可知,当a≤0时,函数f(x)的单调递增区间为(0,+∞),函数f(x)既无极大值也无极小值;
当a>0时,函数f(x)的单调递减区间为(0,),单调递增区间为(,+∞),函数f(x)有极小值,无极大值.
(3)当a≤0时,由(2)知函数f(x)在区间(0,+∞)上单调递增,故函数f(x)在区间(1,e2]内至多有一个零点,不合题意.
当a>0时,由(2)知,当x∈(0,)时,函数f(x)单调递减;当x∈(,+∞)时,函数f(x)单调递增,函数f(x)在(0,+∞)上的最小值为f()=.
若函数f(x)在区间(1,e2]内恰有两个零点,则需满足即整理得
所以e0,y>0,
知+=1,且a>0,b>0,
则x+2y=(x+2y)=2a+8b+4≥2a+8b+4·2,
当且仅当y=x时取等号,
即x+2y的最小值为2a+8b+32,
由条件得2a+8b+32=64,即a+4b=16.
又ab=16,
所以a=8,b=2,故ab=82=64.
答案:64
2.定义运算ab=则关于非零实数x的不等式4≥8的解集为________________________________________________________________________.
解析:当x≤-1时,因为x+<0,x≤,
故原不等式可化为x+≥8x,在(-∞,-1]上恒成立;
当-1,
故原不等式可化为x+≥,在(-1,0)上恒成立;
当04,x<,
故原不等式可化为4≥8x,解得01时,因为x+≥4,x>,
故原不等式可化为4≥,解得x≥2.
综上所述,原不等式的解集为(-∞,0)∪∪[2,+∞).
答案:(-∞,0)∪∪[2,+∞)
3.已知函数y=f(x)(x∈R).对于函数y=g(x)(x∈I),定义g(x)关于f(x)的“对称函数”为函数y=h(x)(x∈I),y=h(x)满足:对任意x∈I,两个点(x,h(x)),(x,g(x))关于点(x,f(x))对称.若h(x)是g(x)=关于f(x)=3x+b的“对称函数”,且h(x)>g(x)恒成立,则实数b的取值范围是________.
解析:由于g(x)=的图象是圆x2+y2=4在x轴上方的半圆(包括与x轴的交点),设这个半圆的一条切线方程为y=3x+b1,则有=2,解得b1=2,要使得h(x)>g(x)恒成立,则需b>b1=2.
故实数b的取值范围为(2,+∞).
答案:(2,+∞)
4.定义区间(a,b),[a,b),(a,b],[a,b]的长度均为d=b-a.用[x]表示不超过x的最大整数,记{x}=x-[x],其中x∈R.设f(x)=[x]·{x},g(x)=x-1,若用d表示不等式f(x)<g(x)解集区间的长度,则当0≤x≤3时,d=________.
解析:f(x)=[x]·{x}=[x]·(x-[x])=[x]x-[x]2,
由f(x)<g(x)得[x]x-[x]2<x-1,
即([x]-1)·x<[x]2-1.
当x∈[0,1)时,[x]=0,
不等式的解为x>1,不合题意;
当x∈[1,2)时,[x]=1,不等式为0<0,无解,不合题意;
当x∈[2,3]时,[x]>1,
所以不等式([x]-1)x<[x]2-1等价于x<[x]+1,此时恒成立,
所以不等式的解为2≤x≤3,
所以当0≤x≤3时,不等式f(x)<g(x)解集区间的长度为d=1.
答案:1
5.已知f(x)是定义在集合M上的函数.若区间D⊆M,且对任意x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭.
(1)判断f(x)=x-1在区间[-2,1]上是否封闭,并说明理由;
(2)若函数g(x)=在区间[3,10]上封闭,求实数a的取值范围;
(3)若函数h(x)=x3-3x在区间[a,b](a,b∈Z,且a≠b)上封闭,求a,b的值.
解:(1)因为函数f(x)=x-1在区间[-2,1]上单调递增,所以当x∈[-2,1]时,f(x)的值域为[-3,0].
而[-3,0]⊄[-2,1],所以函数f(x)在区间[-2,1]上不是封闭的.
(2)因为g(x)==3+.
①当a=3时,函数g(x)=3,显然{3}⊆[3,10],故a=3满足题意;
②当a>3时,在区间[3,10]上,函数g(x)单调递减,此时g(x)的值域为.
由⊆[3,10]得
解得3≤a≤31,故3<a≤31;
③当a<3时,在区间[3,10]上,有g(x)=3+<3,不合题意.
综上所述,实数a的取值范围是[3,31].
(3)因为h(x)=x3-3x,
所以h′(x)=3x2-3=3(x+1)(x-1).
因为当x<-1或x>1时,h′(x)>0;当x=-1或x=1时,h′(x)=0;当-1<x<1时,h′(x)<0,
所以函数h(x)在区间(-∞,-1)上单调递增,在区间(-1,1)上单调递减,在区间(1,+∞)上单调递增.
从而h(x)在x=-1处取得极大值2,在x=1处取得极小值-2.
由题意知
即解得
因为a<b,所以-2≤a≤0,0≤b≤2.
又a,b∈Z,故a只可能取-2,-1,0,b只可能取0,1,2.
①当a=-2时,因为b>0,故由h(-1)=2得b≥2,因此b=2.经检验,a=-2,b=2符合题意;
②当a=-1时,由h(-1)=2,得b=2,此时h(1)=-2∈/[-1,2],不符合题意;
③当a=0时,显然不符合题意.
综上所述,a=-2,b=2.
6.设函数f(x)=x2-(a-2)x-aln x.
(1)求函数f(x)的单调区间;
(2)若函数f(x)有两个零点,求满足条件的最小正整数a的值;
(3)若方程f(x)=c有两个不相等的实数根x1,x2,求证:f′>0.
解:(1)f′(x)=2x-(a-2)-=
=(x>0).
当a≤0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增,所以函数f(x)的单调增区间为(0,+∞),
当a>0时,由f′(x)>0得x>,函数f(x)在上单调递增;由f′(x)<0得0<x<,函数f(x)在上单调递减.
综上可知,当a≤0时,函数f(x)的单调增区间为(0,+∞);当a>0时函数f(x)的单调增区间为,单调减区间为.
(2)由(1)得若函数f(x)有两个零点,则a>0,且f(x)的最小值f<0,即-a2+4a-4
aln<0.
因为a>0,所以a+4ln -4>0.
令h(a)=a+4ln -4,显然h(a)在(0,+∞)上为增函数,且h(2)=-2<0,h(3)=4ln -1=ln -1>0,
所以存在a0∈(2,3),h(a0)=0.
当a>a0时,h(a)>0;当0<a<a0时,h(a)<0.
所以满足条件的最小正整数a=3.
又当a=3时,f(3)=3(2-ln 3)>0,f(2)=2-3ln 2<0,f(1)=0,所以当a=3时,f(x)有两个零点.
综上所述,满足条件的最小正整数a的值为3.
(3)证明:因为x1,x2是方程f(x)=c的两个不相等的实根,由(1)知a>0.不妨设0<x1<x2,
则x-(a-2)x1-aln x1=c,
x-(a-2)x2-aln x2=c.
两式相减得x+2x1-x-2x2=ax1+aln x1-ax2-aln x2=a(x1+ln x1-x2-ln x2).
所以a=.
又因为f′=0,当x∈时,f′(x)<0,当x∈时,f′(x)>0,
故只要证>即可,
即证明x1+x2>,
即证明x-x+(x1+x2)(ln x1-ln x2)<x+2x1-x-2x2,即证明ln<.
设t=(0<t<1).
令g(t)=ln t-,
则g′(t)=-=.
因为t>0,所以g′(t)≥0,当且仅当t=1时,g′(t)=0,所以g(t)在(0,1)上是增函数.
又因为g(1)=0,所以当t∈(0,1)时,g(t)<0总成立.
即不等式ln <总成立,
所以原不等式得证.