- 2021-06-15 发布 |
- 37.5 KB |
- 26页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习 三角恒等变换与解三角形 课件(全国通用)
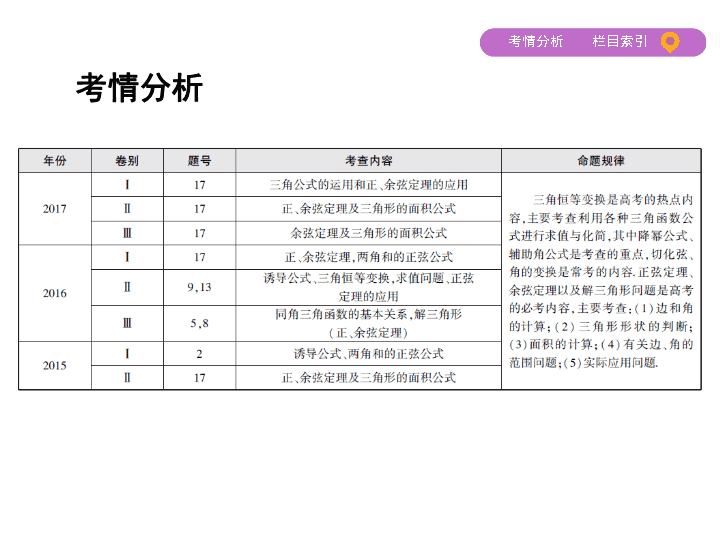
第 2 讲 三角恒等变换与解三角形 考情分析 总纲目录 考点一 三角恒等变换及求值 考点二 正弦定理、余弦定理(高频考点) 考点三 正、余弦定理的实际应用 考点一 三角恒等变换及求值 1.两角和与差的正弦、余弦、正切公式 (1)sin( α ± β )=sin α cos β ± cos α sin β ; (2)cos( α ± β )=cos α cos β ∓ sin α sin β ; (3)tan( α ± β )= . 2.二倍角的正弦、余弦、正切公式 (1)sin 2 α =2sin α cos α ; (2)cos 2 α =cos 2 α -sin 2 α =2cos 2 α -1=1-2sin 2 α ; (3)tan 2 α = . 典型例题 (1)(2017广西三市第一次联考)已知 x ∈(0,π),且cos =sin 2 x ,则 tan 等于 ( ) A. B.- C.3 D.-3 (2)若sin 2 α = ,sin( β - α )= ,且 α ∈ , β ∈ ,则 α + β 的值是 ( ) A. B. C. 或 D. 或 解析 (1)由cos =sin 2 x 得sin 2 x =sin 2 x , ∵ x ∈(0,π),∴tan x =2,∴tan = = . (2)∵ α ∈ ,所以2 α ∈ ,又sin 2 α = ,故2 α ∈ , α ∈ , 所以cos 2 α =- . 又 β ∈ ,故 β - α ∈ , ∴cos( β - α )=- ,∴cos( α + β )=cos[( β - α )+2 α ]=cos( β - α )cos 2 α -sin( β - α )sin 2 α 答案 (1)A (2)A = × - × = , 又 α + β ∈ ,所以 α + β = ,故选A. 方法归纳 三角函数恒等变换“四大策略” (1)常值代换:特别是“1”的代换,1=sin 2 θ +cos 2 θ ,1=tan 45 ° 等; (2)项的分拆与角的配凑:如sin 2 α +2cos 2 α =(sin 2 α +cos 2 α )+cos 2 α , α =( α - β )+ β 等; (3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次; (4)弦切互化:一般是切化弦. 跟踪集训 1.(2017洛阳第一次统一考试)若sin = ,则cos = . 答案 - 解析 cos =cos =-cos =- , 把sin = 代入,原式=- =- . 2.(2017新疆第二次适应性检测) 的值是 . 答案 2 解析 = = = =2. 考点二 正弦定理、余弦定理(高频考点) 命题点 1.利用正、余弦定理求三角形的边长或角的大小. 2.利用正、余弦定理判定三角形的形状. 3.利用正、余弦定理求三角形的面积. 1.正弦定理及其变形 在△ ABC 中, = = =2 R ( R 为△ ABC 的外接圆半径).变形: a =2 R sin A ,sin A = , a ∶ b ∶ c =sin A ∶sin B ∶sin C . 2.余弦定理及其变形 在△ ABC 中, a 2 = b 2 + c 2 -2 bc cos A , b 2 = a 2 + c 2 -2 ac cos B , c 2 = a 2 + b 2 -2 ab cos C . 变形: b 2 + c 2 - a 2 =2 bc cos A ,cos A = , a 2 + c 2 - b 2 =2 ac cos B ,cos B = , a 2 + b 2 - c 2 =2 ab cos C ,cos C = . 3.三角形面积公式 S △ ABC = ab sin C = bc sin A = ac sin B . 典型例题 (2017课标全国Ⅰ,17,12分)△ ABC 的内角 A , B , C 的对边分别为 a , b , c .已知 △ ABC 的面积为 . (1)求sin B sin C ; (2)若6cos B cos C =1, a =3,求△ ABC 的周长. 解析 (1)由题设得 ac sin B = , 即 c sin B = . 由正弦定理得 sin C sin B = . 故sin B sin C = . (2)由题设及(1)得cos B cos C -sin B sin C =- , 即cos( B + C )=- . 所以 B + C = ,故 A = . 由题设得 bc sin A = ,即 bc =8. 由余弦定理得 b 2 + c 2 - bc =9,即( b + c ) 2 -3 bc =9,得 b + c = . 故△ ABC 的周长为3+ . 方法归纳 三角形面积公式的应用原则 (1)对于面积公式 S = ab sin C = ac sin B = bc sin A ,一般是已知哪一个角 就使用哪一个公式. (2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化. 跟踪集训 1.在△ ABC 中, a , b , c 分别是内角 A , B , C 的对边,若 b sin A =3 c sin B , a =3,cos B = ,则 b = ( ) A.14 B.6 C. D. 答案 D 利用正弦定理得 ab =3 bc ,即 a =3 c ,由于 a =3,∴ c =1. 由余弦定理得cos B = = ,∴ b = . 2.在△ ABC 中,角 A , B , C 所对的边分别为 a , b , c ,若查看更多