高三数学（文数）总复习练习专题十六 算法初步

高三数学（文数）总复习练习专题十六 算法初步

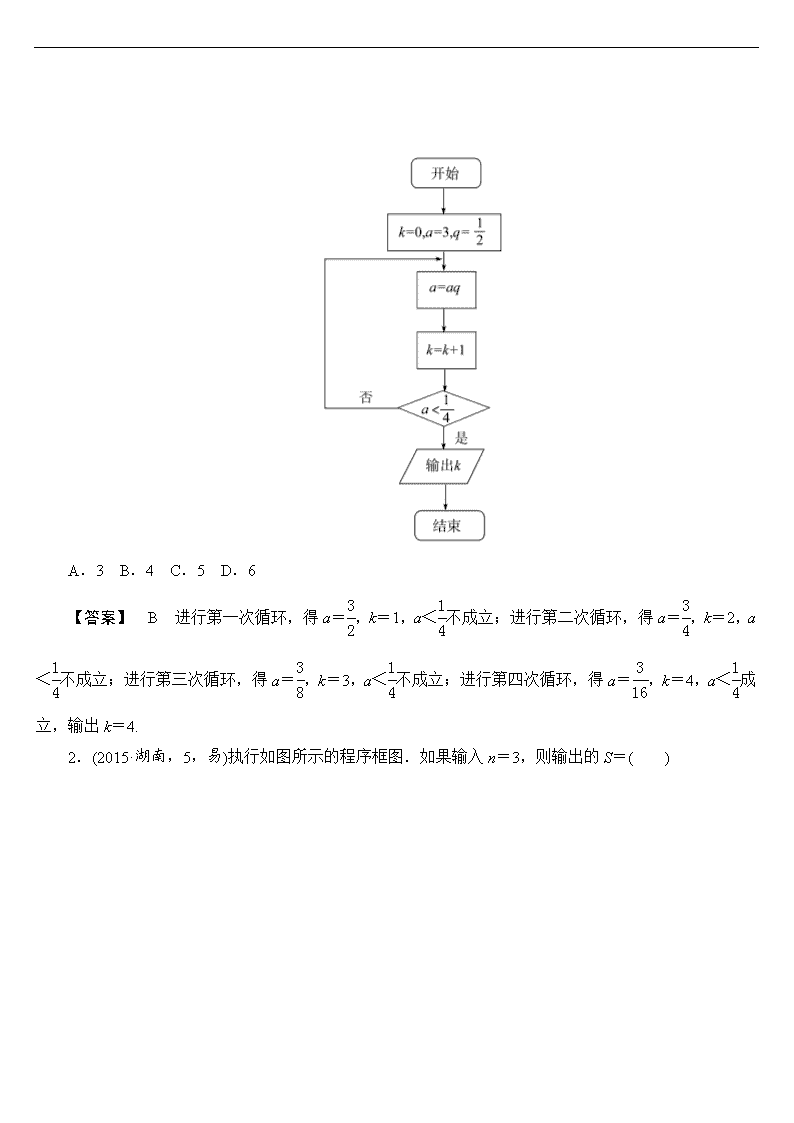
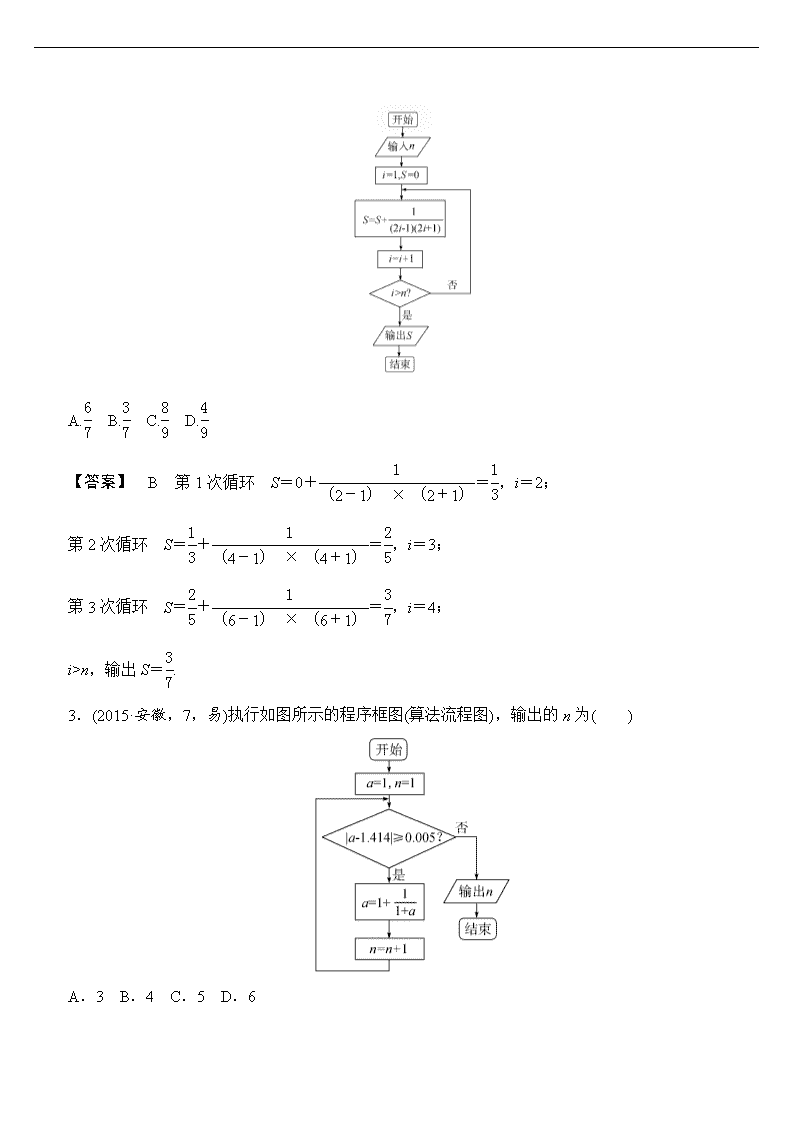
‎1．(2015· 北京，5，易)执行如图所示的程序框图，输出的k值为(　　)‎ A．3 B．4 C．5 D．6‎ ‎【答案】　B　进行第一次循环，得a＝，k＝1，a＜不成立；进行第二次循环，得a＝，k＝2，a＜不成立；进行第三次循环，得a＝，k＝3，a＜不成立；进行第四次循环，得a＝，k＝4，a＜成立，输出k＝4.‎ ‎2．(2015·湖南，5，易)执行如图所示的程序框图．如果输入n＝3，则输出的S＝(　　)‎ A. B. C. D. ‎【答案】　B　第1次循环　S＝0＋＝，i＝2；‎ 第2次循环　S＝＋＝，i＝3；‎ 第3次循环　S＝＋＝，i＝4；‎ i>n，输出S＝.‎ ‎3．(2015·安徽，7，易)执行如图所示的程序框图(算法流程图)，输出的n为(　　)‎ A．3 B．4 C．5 D．6‎ ‎【答案】　B　a＝1，n＝1，‎ 第1步：≥0.005，a＝1＋＝，n＝2；‎ 第2步：＝0.086≥0.005，a＝1＋＝，n＝3；‎ 第3步：＝0.014≥0.005，a＝1＋＝，n＝4；‎ 第4步：≈0.002 6＜0.005，输出n＝4.故选B.‎ ‎4．(2015·课标Ⅱ，8，中)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b分别为14，18，则输出的a＝(　　)‎ A．0 B．2 C．4 D．14‎ ‎【答案】　B　第一步：a＝14，b＝18，则b＝18－14＝4；第二步：a＝14－4＝10；第三步：a＝10－4＝6；第四步：a＝6－4＝2；第五步：b＝4－2＝2，此时a＝b，输出a＝2.‎ ‎5．(2015·课标Ⅰ，9，中)执行如图的程序框图，如果输入的t＝0.01，则输出的n＝(　　)‎ A．5 B．6 C．7 D．8‎ ‎【答案】　C　输入t＝0.01，S＝1，n＝0，m＝，进行第一次循环可得S＝，m＝，n＝1，满足S＞t，进行第二次循环可得S＝，m＝，n＝2，依次下去，直至S＝，m＝，n＝7，不满足S＞t，循环中止，‎ 故最终输出n＝7.选C.‎ ‎6．(2015·山东，11，易)执行如图的程序框图，若输入的x的值为1，则输出的y的值是________．‎ ‎【解析】　当x＝1时，满足x＜2，所以x＝2，不满足x＜2，得y＝3×22＋1＝13，所以输出y的值为13.‎ ‎【答案】　13‎ ‎7．(2015·江苏，4，易)根据如图所示的伪代码，可知输出的结果S为________．‎ S←1‎ I←1‎ While　I<8‎ ‎ S←S＋2‎ ‎ I←I＋3‎ End　While Print　S ‎【解析】　S＝1，I＝1，‎ S＝S＋2＝1＋2＝3，I＝I＋3＝1＋3＝4<8，‎ S＝S＋2＝3＋2＝5，I＝I＋3＝4＋3＝7<8，‎ S＝S＋2＝5＋2＝7，I＝I＋3＝7＋3＝10>8，‎ ‎∴S＝7.‎ ‎【答案】　7‎ ‎1．(2014·北京，4，易)执行如下所示的程序框图，输出的S值为(　　)‎ A．1 B．3 C．7 D．15‎ ‎【答案】　C　k＝0<3，S＝0＋20＝1，k＝1；‎ k＝1<3，S＝1＋21＝3，k＝2；‎ k＝2<3，S＝3＋22＝7，k＝3；‎ k＝3，输出S的值为7.‎ ‎2．(2014·福建，4，易)阅读如图所示的程序框图，运行相应的程序，输出的n的值为(　　)‎ A．1 B．2 C．3 D．4‎ ‎【答案】　B　当n＝1时，21＞12；当n＝2时，22＞22不成立，结束循环，输出n＝2.故选B.‎ ‎3．(2014·陕西，4，易)根据下面框图，对大于2的整数n，输出的数列的通项公式是(　　)‎ A．an＝2n B．an＝2(n－1)‎ C．an＝2n D．an＝2n－1‎ ‎【答案】　C　根据框图可知S＝1，i＝1，执行a1＝2×1＝2，S＝a1＝2，i＝1＋1＝2，判断不符合条件，执行a2＝22，S＝a2＝22，i＝2＋1＝3，判断不符合条件，执行a3＝23，S＝a3＝23，i＝3＋1＝4，…，判断不符合条件，执行an＝2n，S＝an＝2n，i＝n＋1满足条件，输出a1＝2，a2＝22，a3＝23，…，an＝2n，故选C.‎ ‎4．(2014·课标Ⅱ，8，易)执行下面的程序框图，如果输入的x，t均为2，则输出的S＝(　　)‎ A．4 B．5 C．6 D．7‎ ‎【答案】　D　由已知初始值x＝2，t＝2，M＝1，S＝3，k＝1，运算过程如下：‎ 符合k≤2，M＝×2＝2，S＝2＋3＝5，k＝2；‎ 符合k≤2，M＝×2＝2，S＝2＋5＝7，k＝3；‎ 不符合k≤2，此时输出S＝7.‎ ‎5．(2013·陕西，4，易)根据下列算法语句，当输入x为60时，输出y的值为(　　)‎ 输入x；‎ If　x≤50　Then ‎　y＝0.5*x Else ‎　y＝25＋0.6*(x－50)‎ End If 输出y.‎ A．25 B．30 C．31 D．61‎ ‎【答案】　C　由题意，‎ 得y＝ 当x＝60时，y＝25＋0.6(x－50)＝31.‎ ‎6．(2014·四川，6，中)执行如图的程序框图，如果输入的x，y∈R，那么输出的S的最大值为(　　)‎ A．0 B．1 C．2 D．3‎ ‎【答案】　C　记M＝(x，y)．‎ 由程序框图知，当(x，y)∈M时，S＝2x＋y；‎ 当(x，y)∉M时，S＝1.‎ 如图，画出集合M表示的可行域(阴影部分)．‎ 移动直线l0：y＝－2x.‎ 由图可知，当直线l0过点A(1，0)时，目标函数S＝2x＋y取得最大值，此时Smax＝2×1＋0＝2.‎ 所以，当(x，y)∈M时，S的最大值为2＞1，‎ 所以输出的S的最大值为2.故选C.‎ ‎7．(2014·浙江，13，中)若某程序框图如图所示，当输入50时，则该程序运行后输出的结果是________．‎ ‎【解析】　输入50时，n＝50，S＝0，i＝1，然后依次为S＝1，i＝2；S＝4，i＝3；S＝11，i＝4；S＝26，i＝5；S＝57，i＝6，满足S>n，退出循环，所以输出的i的值为6.‎ ‎【答案】　6‎ ‎8．(2014·山东，11，中)执行下面的程序框图，若输入的x的值为1，则输出的n的值为________．‎ ‎【解析】　x＝1，n＝0，12－4×1＋3＝0→x＝2，n＝1，22－4×2＋3＝－1＜0→x＝3，n＝2，32－4×3＋3＝0 →x＝4，n＝3，42－4×4＋3＝3＞0，输出n＝3.‎ ‎【答案】　3‎ ‎9．(2013·湖南，12，中)执行如图所示的程序框图，如果输入a＝1，b＝2，则输出的a的值为________．‎ ‎【解析】　a＝1，b＝2，‎ 第一次循环，a＝a＋b＝1＋2＝3；‎ 第二次循环，a＝a＋b＝3＋2＝5；‎ 第三次循环，a＝a＋b＝5＋2＝7；‎ 第四次循环，a＝a＋b＝7＋2＝9.‎ 因为9>8，所以输出a＝9.‎ ‎【答案】　9‎ ‎10．(2013·四川，18，12分，中)某算法的程序框图如图所示，其中输入的变量x在1，2，3，…，24‎ 这24个整数中等可能随机产生．‎ ‎(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i＝1，2，3)；‎ ‎(2)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i(i＝1，2，3)的频数．以下是甲、乙所作频数统计表的部分数据．‎ 甲的频数统计表(部分)‎ 运行 次数n 输出y的值为1的频数 输出y的值为2的频数 输出y的值为3的频数 ‎30‎ ‎14‎ ‎6‎ ‎10‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎2 100‎ ‎1 027‎ ‎376‎ ‎697‎ 乙的频数统计表(部分)‎ 运行 次数n 输出y的值为1的频数 输出y的值为2的频数 输出y的值为3的频数 ‎30‎ ‎12‎ ‎11‎ ‎7‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎2 100‎ ‎1 051‎ ‎696‎ ‎353‎ 当n＝2 100时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i(i＝1，2，3)的频率(用分数表示)，并判断两位同学中哪一位所编程序符合算法要求的可能性较大．‎ 解：(1)变量x是在1，2，3，…，24这24个整数中随机产生的一个数，共有24种可能．‎ 当x从1，3，5，7，9，11，13，15，17，19，21，23这12个数中产生时，输出y的值为1，故P1＝；‎ 当x从2，4，8，10，14，16，20，22这8个数中产生时，输出y的值为2，故P2＝；‎ 当x从6，12，18，24这4个数中产生时，输出y的值为3，‎ 故P3＝.‎ 所以输出y的值为1的概率为，输出y的值为2的概率为，输出y的值为3的概率为.‎ ‎(2)当n＝2 100时，甲、乙所编程序各自输出y的值为i(i＝1，2，3)的频率如下：‎ 输出y的值为1的频率 输出y的值为2的频率 输出y的值为3的频率 甲 乙 比较频率趋势与概率，可得乙同学所编程序符合算法要求的可能性较大．‎ 考向1　程序框图的执行问题 程序框图的三种基本结构 ‎(1)顺序结构 顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下顺序进行的．程序框图中一定包含顺序结构．‎ ‎(2)条件结构 当需要对研究对象进行逻辑判断时，要使用条件结构，它是根据指定条件选择执行不同指令的控制结构．‎ ‎(3)循环结构 ‎①两种循环结构的特点 直到型循环结构：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．‎ 当型循环结构：在每次执行循环体前，对条件进行判断，当条件满足时，执行循环体，否则终止循环．‎ ‎②利用循环结构表示算法应注意的问题 第一：注意是利用当型循环结构，还是直到型循环结构；‎ 第二：注意选择准确的表示累计的变量；‎ 第三：注意在哪一步开始循环，满足什么条件不再执行循环体．‎ ‎(1)(2013·课标Ⅰ，7)执行下面的程序框图，如果输入的t∈[－1，3]，则输出的s属于(　　)‎ A．[－3，4] B．[－5，2]‎ C．[－4，3] D．[－2，5]‎ ‎(2)(2014·安徽，4)如图所示，程序框图(算法流程图)的输出结果是(　　)‎ A．34 B．55 C．78 D．89‎ ‎【解析】　(1)由框图可知s＝ 当－1≤t＜1时，－3≤s＜3；‎ 当1≤t≤3时，s＝4t－t2＝－(t－2)2＋4，‎ 所以－3≤s≤4.‎ 综上，s∈[－3，4]．‎ ‎(2)运算过程如下：‎ x＝1，y＝1，z＝2，满足z≤50；‎ x＝1，y＝2，z＝3，满足z≤50；‎ x＝2，y＝3，z＝5，满足z≤50；‎ x＝3，y＝5，z＝8，满足z≤50；‎ x＝5，y＝8，z＝13，满足z≤50；‎ x＝8，y＝13，z＝21，满足z≤50；‎ x＝13，y＝21，z＝34，满足z≤50；‎ x＝21，y＝34，z＝55，不满足z≤50，‎ 此时输出55.‎ ‎【答案】　(1)A　(2)B ‎ 1.有关条件结构的应用技巧 ‎(1)条件结构一般用在需要对条件进行判断的算法程序中，如求分段函数的函数值等．‎ ‎(2)含有条件结构的程序框图，体现了分类讨论思想．‎ ‎(3)含有嵌套的条件结构，一定要分清外层条件与内层条件及上下逻辑关系．‎ ‎2．循环结构的应用 循环结构常常用在一些有规律的科学计算中，如累加求和，累乘求积，多次输入等．利用循环结构表示算法：第一要选择准确的表示累计的变量，第二要注意在哪一步结束循环．解答循环结构的程序(算法)框图，最好的方法是完整执行每一次循环，防止执行程序不彻底，造成错误．‎ ‎(2013·辽宁，8)执行如图所示的程序框图，若输入n＝8，则输出S＝(　　)‎ A. B. C. D. ‎【答案】　A　＝＝.‎ 由程序框图知，‎ 第一步：S＝0＋，i＝4；‎ 第二步：S＝0＋＋，i＝6；‎ 第三步：S＝0＋＋＋，i＝8；‎ 第四步：S＝0＋＋＋＋，i＝10.‎ 输出S＝0＋＋＋＋ ‎＝× ‎＝× ‎＝.故选A.‎ 考向2　程序框图的补全问题及逆向求解法 ‎(1)(2013·江西，7)阅读如下程序框图，如果输出i＝4，那么空白的判断框中应填入的条件是(　　)‎ A．S＜8 B．S＜9 C．S＜10 D．S＜11‎ ‎(2)(2013·重庆，8)执行如图所示的程序框图，如果输出s＝3，那么判断框内应填入的条件是(　　)‎ A．k≤6 B．k≤7 ‎ C．k≤8 D．k≤9‎ ‎【解析】　(1)i＝2时，S＝2×2＋1＝5，不满足条件；‎ 当i＝3时，S＝2×3＋2＝8，不满足条件；‎ 当i＝4时，S＝2×4＋1＝9，此时输出i＝4，所以填S＜9.‎ ‎(2)第一步，s＝s·logk(k＋1)＝log23，k＝2＋1＝3；‎ 第二步，s＝s·logk(k＋1)＝log23·log34＝log24，k＝3＋1＝4；‎ 第三步，s＝s·logk(k＋1)＝log24·log45＝log25，k＝5；‎ ‎…‎ 第n步，s＝log2(n＋1)·log(n＋1)(n＋2)＝log2(n＋2)，k＝n＋2，‎ 若输出s＝3，则log2(n＋2)＝3，n＋2＝8，‎ n＝6，k＝n＋2＝8，说明k＝8时结束，故应填k≤7.选B.‎ ‎【答案】　(1)B　(2)B ‎【点拨】　解答本题的关键是搞清进入或退出循环的条件，循环的次数．‎ ‎ 程序框图的补全问题及逆向求解问题的解决办法 解答这类题目时，一定要理解悟透各种框图的作用，才能得到正确的结果，特别要注意对问题的转化，问题与框图的表示的相互转化．‎ ‎(2013·福建，8)阅读如图所示的程序框图，运行相应的程序．如果输入某个正整数n后，输出的S∈(10，20)，那么n的值为(　　)‎ A．3 B．4 C．5 D．6‎ ‎【答案】　B　k＝1时，S＝1；k＝2时，S＝1＋2；‎ k＝3时，S＝1＋2×(1＋2)＝1＋2＋22；‎ k＝4时，S＝1＋2×(1＋2＋22)＝1＋2＋22＋23.‎ 由此可知框图的功能为求和，‎ 即S＝1＋21＋22＋…＋2n－1＝＝2n－1，‎ 令2n－1∈(10，20)，‎ 得10＜2n－1＜20，即11＜2n<21，‎ ‎∴n＝4.‎ ‎∴判断框内的条件为k＞4，即n＝4.故选B.‎ ‎1．(2015·广东东莞一模，5)执行如图所示的程序框图，输出的值为(　　)‎ A．1 B．－1 C．－2 D．0‎ ‎【答案】　D　T＝0，S＝1⇒T＝1，S＝0⇒T＝1，S＝－1⇒T＝0，S＝－1⇒T＝－1，S＝0.‎ ‎2．(2014·安徽蚌埠一模，6)执行如图所示的程序框图，若输出的n＝5，则输入整数p的最小值是(　　)‎ A．15 B．14‎ C．7 D．8‎ ‎【答案】　D　程序在运行过程中各变量的值如下表示：‎ 是否继续循环　　 S　　 n 循环前 0 1‎ 第一次循环 是 1 2‎ 第二次循环 是 3 3‎ 第三次循环 是 7 4‎ 第四次循环 是 15 5‎ 第五次循环 否 故当S值不大于7时继续循环，大于7但不大于15时退出循环，故p的最小整数值为8.‎ ‎3．(2014·河北秦皇岛一模，9)下图给出的是计算＋＋＋…＋的值的一个框图，其中菱形判断框内应填入的条件是(　　)‎ A．i＞10 B．i＜10‎ C．i＞11 D．i＜11‎ ‎【答案】　A　经过第一次循环得到s＝，‎ i＝2，此时的i不满足判断框中的条件；‎ 经过第二次循环得到s＝＋，i＝3，此时的i不满足判断框中的条件；‎ 经过第三次循环得到s＝＋＋，i＝4，此时的i不满足判断框中的条件；‎ ‎……‎ 经过第十次循环得到s＝＋＋＋…＋，i＝11，此时的i满足判断框中的条件，执行输出，故判断框中的条件是i＞10.‎ ‎4．(2015·湖南岳阳一模，5)执行如图所示的程序框图后，输出的值为4，则p的取值范围是(　　)‎ A.＜p≤ B．p＞ C.≤p＜ D.＜p≤ ‎【答案】　D　执行程序框图依次得S＝，n＝2；S＝，n＝3；S＝，n＝4，此时应不满足条件，故选D.‎ ‎5．(2015·河南新乡质检，7)执行如图所示的程序框图，输出的k的值为(　　)‎ A．4 B．5 C．6 D．7‎ ‎【答案】　A　S＝0＋20＝1＜100，k＝2；‎ S＝1＋21＝3＜100，k＝3；‎ S＝3＋23＝11＜100，k＝4；‎ S＝11＋211＞100，∴输出k＝4.‎ ‎6．(2015·湖北孝感一模，8)阅读如图所示的程序框图，若输入的N＝100，则输出的结果是(　　)‎ A．50 B. C．51 D. ‎【答案】　A　i＝1，N＝100，i＞N不成立，执行第一次循环，S＝0＋1＝1，i＝1＋1＝2；‎ i＞N不成立，执行第二次循环，S＝1＋2＝3，i＝2＋1＝3；‎ i＞N不成立，执行第三次循环，S＝1＋2＋3＝6，i＝3＋1＝4；…；‎ i＞N不成立，执行第一百次循环，S＝1＋2＋3＋…＋100＝，‎ i＝100＋1＝101；‎ i＞N成立，输出＝×＝50，故选A.‎ ‎7．(2014·河北衡水中学一模，13)某程序框图如图所示，对应的程序运行后输出的S的值是________．‎ ‎【解析】　S＝2，i＝1；‎ S＝＝－3，i＝2；‎ S＝＝－，i＝3；‎ S＝＝，i＝4；‎ S＝＝2，i＝5；…；‎ 当i＝2 011时，输出S，2 011除以4等于502余3，所以输出S＝－.‎ ‎【答案】　－ ‎8．(2015·山东济南一模，14)阅读如图所示的程序框图，运行相应的程序，则输出的结果是________．‎ ‎【解析】　S＝sin ＋sin π＋sin ＋‎ sin 2π＋…＋sin ＋sin 1 005π＋‎ sin ＋sin 1 006π＋sin ＝1.‎ ‎【答案】　1‎ ‎(时间：45分钟__分数：80分)‎ 一、选择题(共12小题，每小题5分，共60分)‎ ‎1．(2014·湖北武汉三模，3)阅读下边的程序框图，运行相应的程序．若输入x的值为1，则输出S的值为(　　)‎ A．64 B．73 C．512 D．585‎ ‎【答案】　B　①x＝1，S＝0⇒S＝0＋13＝1；‎ ‎②x＝2⇒S＝1＋23＝9；‎ ‎③x＝4⇒S＝9＋43＝73＞50，所以输出S的值为73，故选B.‎ ‎2．(2014·课标Ⅰ，9)执行下面的程序框图，若输入的a，b，k分别为1，2，3，则输出的M＝(　　)‎ A. B. C. D. ‎【答案】　D　当n＝1时，M＝，a＝2，b＝；‎ 当n＝2时，M＝，a＝，b＝；‎ 当n＝3时，M＝，a＝，b＝；‎ 当n＝4时，终止循环，输出M＝.‎ 注意：a＝b，b＝M中的“＝”是赋值号．‎ ‎3．(2014·吉林长春三模，8)某算法的程序框图如图所示，该算法的功能是(　　)‎ A．计算(1＋20)＋(2＋21)＋(3＋22)＋…＋(n＋1＋2n)的值 B．计算(1＋21)＋(2＋22)＋(3＋23)＋…＋(n＋2n)的值 C．计算(1＋2＋3＋…＋n)＋(20＋21＋22＋…＋2n－1)的值 D．计算[1＋2＋3＋…＋(n－1)]＋(20＋21＋22＋…＋2n)的值 ‎【答案】　C　初始值k＝1，S＝0，第1次进入循环体：S＝1＋20，k＝2；‎ 当第2次进入循环体：S＝1＋20＋2＋21，k＝3，…，给定正整数n，当k＝n时，最后一次进入循环体，则有S＝1＋20＋2＋21＋…＋n＋2n－1，k＝n＋1，退出循环体，输出S＝(1＋2＋3＋…＋n)＋(20＋21＋22＋…＋2n－1)，故选C.‎ ‎4．(2015·湖南湘潭一模，7)执行如图所示的程序框图，如果输入a＝2，b＝2，那么输出的a值为(　　)‎ A．4 B．16‎ C．256 D．log316‎ ‎【答案】　C　log32＞4不成立，执行第一次循环，a＝22＝4；‎ log34＞4不成立，执行第二次循环，a＝42＝16；‎ log316＞4＝log334＝log381不成立，执行第三次循环，a＝162＝256；‎ log3256＞4＝log381成立，跳出循环体，输出a的值为256，故选C.‎ ‎5．(2013·浙江，5)某程序框图如图所示，若该程序运行后输出的值是，则(　　)‎ A．a＝4 B．a＝5 ‎ C．a＝6 D．a＝7‎ ‎【答案】　A　方法一：由程序框图及最后输出的值是可知，当k＝1时，S＝1，k＞a不成立，故S＝1＋＝，k＝2＞a不成立，故S＝＋＝，k＝3＞a不成立，故S＝＋＝，k＝4＞a不成立，故S＝‎ ＋＝，此时k＝5＞a成立，所以a＝4.‎ 方法二：由程序框图可知，‎ S＝1＋＋＋…＋＝1＋1－＋－＋…＋－＝1＋1－＝2－，由S＝，得2－＝，解得k＝4，故由程序框图可知k＝4＞a不成立，k＝5＞a成立，所以a＝4.‎ ‎6．(2014·湖南，7)执行如图所示的程序框图，如果输入的t∈[－2，2]，则输出的S属于(　　)‎ A．[－6，－2] B．[－5，－1]‎ C．[－4，5] D．[－3，6]‎ ‎【答案】　D　当－2≤t＜0时，由t＝2t2＋1得1＜t≤9，此时S＝t－3∈(－2，6]；‎ 当0≤t≤2时，S＝t－3∈[－3，－1]．‎ 综上，S∈[－3，6]，故选D.‎ ‎7．(2012·陕西，5)如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图，则图中空白框内应填入(　　)‎ A．q＝ B．q＝ C．q＝ D．q＝ ‎【答案】　D　由框图知xi≥60的人数为M，xi＜60的人数为N，故空白处填q＝.‎ ‎8．(2015·山西大同调研，8)如图的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的(　　)‎ A．c＞x? B．x＞c? ‎ C．c＞b? D．b＞c?‎ ‎【答案】　A　由于要取a，b，c中最大的数，则输出的x应当是a，b，c中最大的数．第一个循环语句是将a，b中的大值赋给x，所以空白判断框中应填比较x与c大小的语句，结合各选项知选A.‎ ‎9．(2015·湖北七市联考，6)如图所示，程序框图输出的所有实数对(x，y)所对应的点都在函数(　　)‎ A．y＝x＋1的图象上 B．y＝2x的图象上 C．y＝2x的图象上 D．y＝2x－1的图象上 ‎【答案】　D　由程序框图可知输出的实数对(x，y)为(1，1)，(2，2)，(3，4)，(4，8)，这些点都在函数y＝2x－1的图象上．‎ ‎10．(2015·江西八所重点高中联考，8)已知如图所示的程序框图(未完成)，设当箭头a指向①时，输出的结果为S＝m，当箭头a指向②时，输出的结果为S＝n，则m＋n＝(　　)‎ A．20 B．15 C．5 D．10‎ ‎【答案】　A　当箭头a指向①时：i＝1，S＝1；i＝2，S＝2；i＝3，S＝3；i＝4，S＝4；i＝5，S＝5；i＝6，结束循环，输出结果S＝m＝5；当箭头a指向②时：i＝1，S＝1；i＝2，S＝1＋2；i＝3，S＝1＋2＋3；i＝4，S＝1＋2＋3＋4；i＝5，S＝1＋2＋3＋4＋5；i＝6，结束循环，输出结果S＝n＝1＋2＋3＋4＋5＝15，故m＋n＝20.‎ ‎11．(2015·河北秦皇岛二模，9)某班有24名男生和26名女生，数据a1，a2，…，a50是该班50名学生在一次数学学业水平模拟考试中的成绩(成绩不为0)，如图所示的程序用来同时统计全班成绩的平均分：A，男生平均分：M，女生平均分：W.为了便于区别性别，输入时，男生的成绩用正数，女生的成绩用其成绩的相反数，那么在图中空白的判断框和处理框中，应分别填入(　　)‎ A．T＞0？，A＝ B．T＜0？，A＝ C．T＜0？，A＝ D．T＞0？，A＝ ‎【答案】　D　依题意得，全班成绩的平均数应等于班级中所有的学生的成绩总和除以总人数，注意到当T＞0时，输入的是某男生的成绩；当T＜0时，输入的是某女生的成绩的相反数．结合题意得，选D.‎ ‎12．(2015·安徽合肥调研，7)定义某种运算S＝a⊗b，运算原理如图所示，则式子：‎ －的值是(　　)‎ A．－3 B．－4 C．－8 D．0‎ ‎【答案】　D　由题意可知，程序框图的运算原理可视为函数S＝a⊗b＝ 所以⊗ln e＝2⊗1＝4，‎ lg 100⊗＝2⊗3＝4，‎ 所以 ‎－＝4－4＝0，‎ 故选D.‎ 二、填空题(共4小题，每小题5分，共20分)‎ ‎13．(2012·江苏，4)如图是一个算法流程图，则输出的k的值是________．‎ ‎【解析】　∵k2－5k＋4＞0，∴k＞4或k＜1，则当k＝5时，循环终止，∴k＝5.‎ ‎【答案】　5‎ ‎14．(2014·辽宁，13)执行下面的程序框图，若输入n＝3，则输出T＝________.‎ ‎【解析】　i＝1时，S＝1，T＝1；i＝2时，S＝3，T＝4；i＝3时，S＝6，T＝10；i＝4时，S＝10，T＝20，i＝4＞3，∴输出T＝20.‎ ‎【答案】　20‎ ‎15．(2013·湖北，12)阅读如图所示的程序框图，运行相应的程序，输出的结果i＝________.‎ ‎【解析】　程序框图的执行流程及中间结果如下：‎ 第一步：a＝10，i＝1，a≠4，a不是奇数，a＝＝5，i＝2；‎ 第二步：a≠4，a是奇数，a＝3×5＋1＝16，i＝3；‎ 第三步：a≠4，a不是奇数，a＝＝8，i＝4；‎ 第四步：a≠4，a不是奇数，a＝＝4，i＝5；‎ 第五步：a＝4，这时跳出循环，输出i＝5.‎ ‎【答案】　5‎ ‎16．(2015·山东临沂一模，14)如图①是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图，已知图①中从左向右第一组的频数为4 000.在样本中记月收入在[1 000，1 500)，[1 500，2000)，[2 000，2 500)，[2 500，3 000)，[3 000，3 500)，[3500，4000)的人数依次为A1，A2，…，A6.图②是统计图①中月工资收入在一定范围内的人数的程序框图，则样本的容量n＝________；图②输出的S＝________.(用数字作答)‎ ‎【解析】　由图可知月收入在[1 000，1 500)的频率为0.000 8×500＝0.4，且有4 000人，故样本容量n＝＝10 000.‎ 由图②知输出的S＝A2＋A3＋…＋A6＝10 000－4 000＝6 000(人)．‎ ‎【答案】　10 000　6 000‎