数学理卷·2017届广东省普宁英才华侨中学高三上学期第三次月考(2016
普宁英才华侨中学2016-2017学年度第一学期第三次月考
高三数学(理科)
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号等相关信息填写在答题卷密封线内,并在“座位号”栏内填写座位号。
2. 所有题目必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷上各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
一、 选择题
1. 定义在R上的函数 ,满足 ,若 且 ,则有( )
A. B. C. D.不能确定
2. 已知函数 .下列命题:( )
①函数 的图象关于原点对称; ②函数 是周期函数;
③当 时,函数 取最大值;④函数 的图象与函数 的图象没有公共点,其中正确命题的序号是
A.①③ B.②③ C.①④ D.②④
3. 若曲线 在点 处的切线平行于x轴,则k= ( )
A.-1 B.1 C.-2 D.2
4. 若点 在函数 的图像上,点 在函数 的图像上,则 的最小值为( )
A. B.2 C. D.8
5. 已知 为 上的可导函数,且 ,均有 ,则以下判断正确的是
A. B.
C. D. 大小无法确定
6.若在上是减函数,则的取值范围是( )
A. B.
C. D.
7.在等比数列中,若,,的前项和为,则( )
A. B.2 C. D.
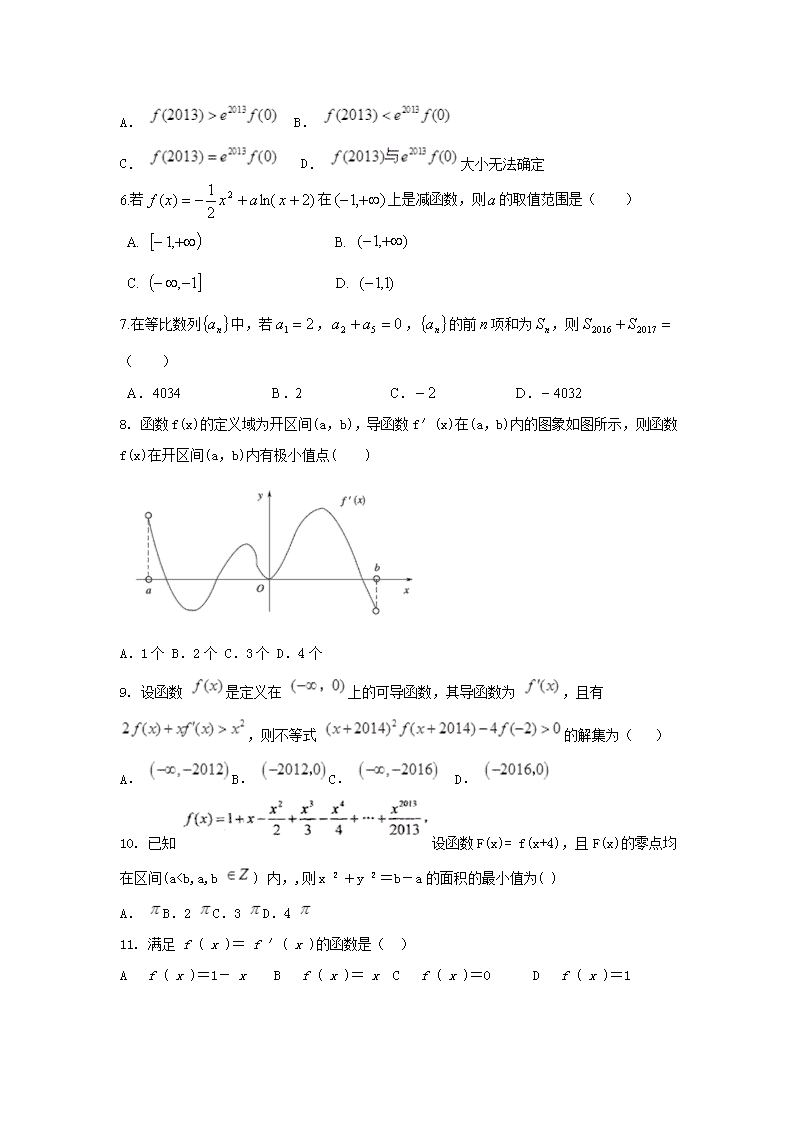
8. 函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
A.1个 B.2个 C.3个 D.4个
9. 设函数 是定义在 上的可导函数,其导函数为 ,且有 ,则不等式 的解集为( )
A. B. C. D.
10. 已知 设函数F(x)= f(x+4),且F(x)的零点均在区间(a
0,ω>0)的图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和.
(1)求函数f(x)的解析式;
(2)求sin的值.
19. (本小题满分12分)
已知正项数列的前项和为,且是与的等差中项.
(Ⅰ)求数列的通项公式;
(Ⅱ)设为数列的前项和,证明:.
20. (本小题满分12分)
已知函数.
(Ⅰ)当时,求曲线在处的切线方程;
(Ⅱ)当时,若不等式恒成立,求实数的取值范围.
21. (本小题满分12分)
设函数f(x)=ax2-a-lnx,其中a∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当时,恒成立,求a的取值范围. (其中,e=2.718…为自然对数的底数).
请考生在第22、23二题中任选一题做答,如果多做,则按所做的第一题计分。
做答时请写清题号。
22.(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标的极点在直角坐标系的原点处,极轴与x轴非负半轴重合,直线l
的参数方程为:(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程和直线l的普通方程;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值.
23.(本小题满分12分)选修4-5:不等式选讲
已知函数,.
(Ⅰ)解不等式;
(Ⅱ)若对任意的,都有,使得成立,求实数的取值范围.
普宁英才华侨中学2016-2017学年度第一学期第三次月考
高三数学参考答案(理科)
1、 A
2、 C
3、 A
4、 D
5、 B
6、 A
7、 C
8、 A
9、 C
10、 A
11、 C
12、B
13. 14. 15. 6 16.
17.解:(Ⅰ)把的坐标代入,得 ………2分
解得. ………………………………5分
(Ⅱ)由(Ⅰ)知,
所以. ………………………………6分
此函数的定义域为R,又, ……9分
所以函数为奇函数. ………………………………10分
18解: .(本小题满分12分) (1)由题意可得A=2,-x0=,所以T=π.
由=π,得ω=2,所以f(x)=2sin.
(2)因为点(x0,2)是函数f(x) =2sin在y轴右侧的第一个最高点,
所以2x0+.所以x0=.
所以sin=sin
=sincos+cossin
==.
19. (1)时, ————————1分
时,,又,两式相减得为是以1为首项,2为公差的等差数列,即. ————————6分
(2)
,
——————10
又,
综上成立. ————————12分
20.(1)当时,,
即曲线在处的切线的斜率为,又,
所以所求切线方程为. ————————4分
(2)当时,若不等式恒成立
易知
若,则恒成立,在R上单调递增;
又,所以当时,,符合题意. —————6分
若,由,解得,则当时,,单调递减;
当时,,单调递增.
所以时,函数取得最小值. ————————8分
则当,即时,则当时,,符合题意.
————————10分
当,即时,则当时,单调递增,,不符合题意.
综上,实数的取值范围是 ————————12分(没有综上扣一分)
21.(1)由题意得:
当时,上单调递减.
当时,,当时,,
当时,故在上单调递减,在上单调递增. ————————5分
(2)原不等式等价于在上恒成立,
一方面,令
只需在上恒大于0即可,
又,故在处必大于等于0.
令可得. ————————8分
另一方面,当时,
又,,,故在时恒大于0,
当时,在单调递增.
故也在单调递增.
即在上恒大于0. .
综上,. ————————12分(没有综上扣一分)
22.本题满分10分
解:(1)∵ρ=4cosθ.
∴ρ2=4ρcosθ,
由ρ2=x2+y2,ρcosθ=x,得x2+y2=4x, 3分
所以曲线C的直角坐标方程为(x-2)2+y2=4,
消去t解得:.所以直线l的普通方程为. 5分
(2)把代入x2+y2=4x.
整理得t2-3t+5=0.
设其两根分别为t1,t2,则t1+t2=3,t1t2=5.
所以|PQ|=|t1-t2|==. 10分
23、本题满分10分
解析:
(1)由得, ,解得 .
所以原不等式的解集为 5分
(2)因为对任意,都有,使得=成立
所以,
有,
所以从而 或 10分