- 2021-06-15 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市16区县2017届高三上学期期末考试数学试题分类汇编-三角函数 Word版
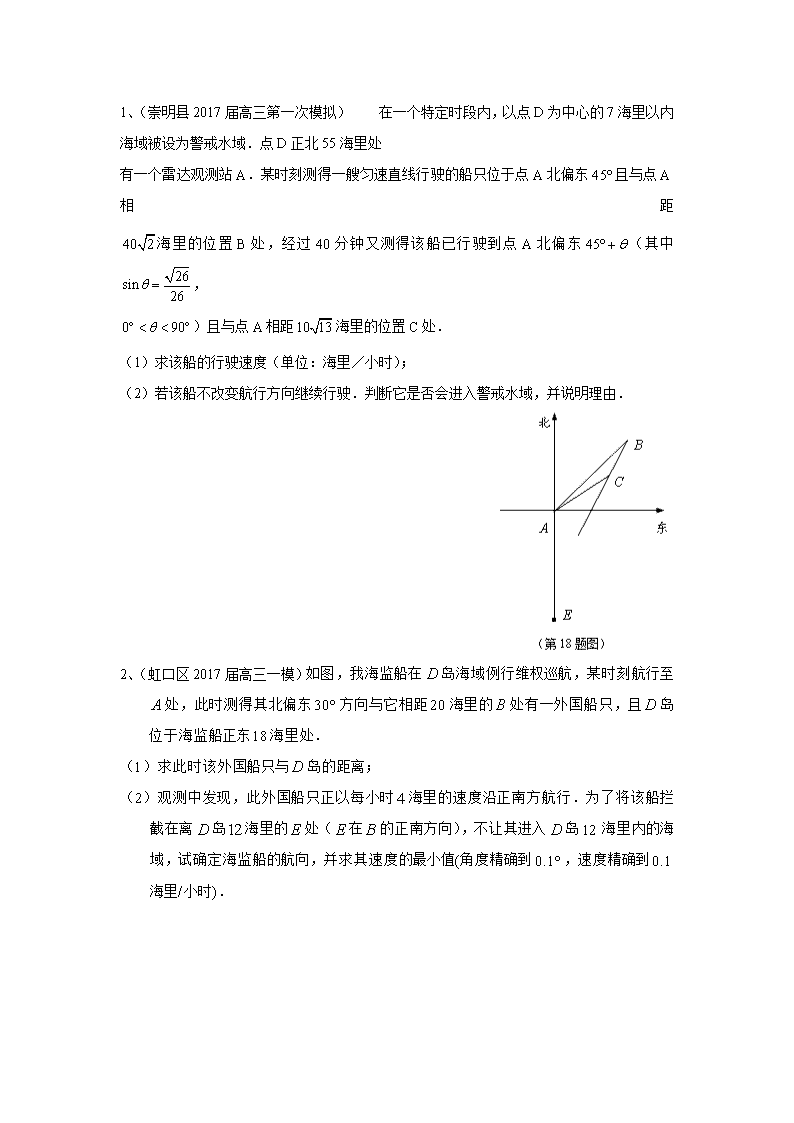
上海市各区县 2017 届高三上学期期末考试数学试题分类汇编 三角函数 一、填空、选择题 1、(宝山区 2017 届高三上学期期末)若函数 的最小正周期为 ,则实 数 的值为 2、(崇明县 2017 届高三第一次模拟)已知 A,B 分别是函数 在 轴右 侧图像上的第一个最高点和第一个最低点,且 ,则该函数的最小正周期是 . 3、(虹口区 2017 届高三一模)设函数 ,且 ,则 . 4、(黄浦区 2017 届高三上学期期终调研)已知 , ,则 的值 为 . 5、(静安区 2017 届向三上学期期质量检测)函数 的最小正周期 为 . 6、(闵行区 2017 届高三上学期质量调研) 曲线 : ,曲线 : ,它们交点的个数 ( ) (A) 恒为偶数 (B) 恒为奇数 (C) 不超过 (D) 可超过 7 、 ( 浦 东 新 区 2017 届 高 三 上 学 期 教 学 质 量 检 测 ) 函 数 的最小正周期为____________. 8、(普陀区 2017 届高三上学期质量调研) 若 , ,则 . 9 、( 青 浦 区 2017 届 高 三 上 学 期 期 末 质 量 调 研 ) 已 知 , 现从集合 中任取两个不同元素 、 ,则使得 的可 能情况为 …………………( ). A. 种 B. 种 C. 种 D. 种 cos sin sin cos x xy x x = aπ a 2sin) ( 0( )f x xω ω >= y 2AOB π∠ = ( ) sin cosf x x x= − ( ) 1f α = sin2α = π 1sin( )2 3 α + = π( ,0)2 α ∈ − tanα +−= 4sin31)( 2 π xxf 1C siny x= 2C ( )2 2 21 02x y r r r + + − = > 2017 2017 ( ) ( )( )3sin cos 3 cos sinf x x x x x= + − 22 παπ <<− 5 3sin =α =α2cot ( ) sin 3f x x π= {1,2,3,4,5,6,7,8}A = A s t ( ) ( ) 0f s f t⋅ = 12 13 14 15 10 、(松 江 区 2017 届 高 三 上 学 期 期 末 质 量 监 控 ) 已 知 向 量 , ,则函数 的最小正周期为 ▲ . 11、(杨浦区 2017 届高三上学期期末等级考质量调研)若 中, , , 则 面积的最大值是_________. 12、(长宁、嘉定区 2017 届高三上学期期末质量调研)函数 ( )的 最小正周期是 ,则 ____________. 13、(虹口区 2017 届高三一模)已知函数 在区间 (其中 ) 上单调递增,则实数 的取值范围是( ). 14、(静安区 2017 届向三上学期期质量检测)已知 为锐角,且 ,则 ________ . 15、(浦东新区 2017 届高三上学期教学质量检测)将 图像向左平移 个单位, 所得的函数为( ). A. B. C. D. 16、(奉贤区 2017 届高三上学期期末)已知函数 , 若函数 在区间 内单调递增,且函数 的图像关于直线 对称,则 的值为____________. 17、(金山区 2017 届高三上学期期末)如果 ,且 为第四象限角,则 的 值是 α 3cos( )4 5 πα + = sinα = (sin ,cos )a x x= (sin ,sin )b x x= ( )f x a b= ⋅ ABC△ 4a b+ = 30C∠ = ° ABC△ −= 3sin πωxy 0>ω π =ω ( ) sin(2 )3f x x π= + [ ]0, a 0a > a .A 0 2a< ≤ π .B 0 12a π< ≤ .C ,12a k k N ππ ∗= + ∈ .D 2 2 ,12k a k k N< ≤ + ∈ππ π cos2y x= 6 π cos 2 3y x π = + cos 2 6y x π = + cos 2 3y x π = − cos 2 6y x π = − ( ) ( )sin cos 0 ,f x wx wx w x R= + > ∈ ( )f x ( ),ω ω− ( )f x x ω= ω 5sin 13 α = − α tanα 二、解答题 1、(崇明县 2017 届高三第一次模拟) 在一个特定时段内,以点 D 为中心的 7 海里以内 海域被设为警戒水域.点 D 正北 55 海里处 有一个雷达观测站 A.某时刻测得一艘匀速直线行驶的船只位于点 A 北偏东 且与点 A 相 距 海里的位置 B 处,经过 40 分钟又测得该船已行驶到点 A 北偏东 (其中 , )且与点 A 相距 海里的位置 C 处. (1)求该船的行驶速度(单位:海里/小时); (2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由. 2、(虹口区 2017 届高三一模)如图,我海监船在 岛海域例行维权巡航,某时刻航行至 处,此时测得其北偏东 方向与它相距 海里的 处有一外国船只,且 岛 位于海监船正东 海里处. (1)求此时该外国船只与 岛的距离; (2)观测中发现,此外国船只正以每小时 海里的速度沿正南方航行.为了将该船拦 截在离 岛 海里的 处( 在 的正南方向),不让其进入 岛 12 海里内的海 域,试确定海监船的航向,并求其速度的最小值(角度精确到 ,速度精确到 海里/小时). 45° 40 2 45 θ° + 26sin 26 θ = 0 90θ° < < ° 10 13 D A 30° 20 B D 18 D 4 D 12 E E B D 0.1° 0.1 3、(黄浦区 2017 届高三上学期期终调研)现有半径为 、圆心角 为 的扇形材 料,要裁剪出一个五边形工件 ,如图所示.其中 分别在 上, 在 上,且 , , .记 ,五边形 的 面积为 . (1)试求 关于 的函数关系式; (2)求 的最大值. 4、(静安区 2017 届向三上学期期质量检测)在某海滨城市附近海面有一台风,据监测,当 前台风中心位于城市 A(看做一点)的东偏南 角方向 ,300 km 的海面 P 处, 并以 20km / h 的速度向西偏北 45°方向移动.台风侵袭的范围为圆形区域,当前半径为 60 km,并以 10km / h 的速度不断增大. (1) 问 10 小时后,该台风是否开始侵袭城市 A,并说明理由; (2) 城市 A 受到该台风侵袭的持续时间为多久? R ( )AOB∠ 90° OECDF ,E F ,OA OB ,C D AB OE OF= EC FD= ECD∠ = 90CDF∠ = ° 2COD θ∠ = OECDF S S θ S θ 2cos 10 θ = 5、(浦东新区 2017 届高三上学期教学质量检测)已知 的内角 的对边分别为 . (1)若 的面积 ,求 值; (2)若 ,求角 . 6、(青浦区 2017 届高三上学期期末质量调研) 已知函数 . (1) 求函数 在区间 上的最大值; (2)在 中,若 ,且 ,求 的值. 7、(松江区 2017 届高三上学期期末质量监控)上海市松江区天马山上的“护珠塔”因其倾斜 度超过意大利的比萨斜塔而号称“世界第一斜塔” .兴趣小组同学实施如下方案来测量塔的 倾斜度和塔高:如图,记 O 点为塔基、P 点为塔尖、点 P 在地面上的射影为点 H.在塔身 OP 射影所在直线上选点 A,使仰角 ,过 O 点与 OA 成 的地面上选 B 点,使 仰角 (点 A、B、O 都在同一水平面上),此时测得 ,A 与 B 之 间距离为 米.试求: (1)塔高(即线段 PH 的长,精确到 0.1 米); (2)塔身的倾斜度(即 PO 与 PH 的夹角,精确到 ). ABC∆ , ,A B C , ,a b c , 7,3B b ABC π= = ∆ 3 3 2S = a c+ ( ) 22cosC BA BC AB AC c+ = C ( ) ( )2 2 1 33sin cos 4 2f x x x x π + = + − − ∈ R ( )f x 0, 2 π ABC∆ A B< ( ) ( ) 1 2f A f B= = BC AB 45HAP °∠ = 120° 45HBP °∠ = 27OAB∠ = 33.6 0.1 8、(徐汇区 2017 届高三上学期学习能力诊断)已知函数 . (1)当 时,求 的值域; (2)已知 的内角 的对边分别为 ,若 , 求 的面积. 9、(长宁、嘉定区 2017 届高三上学期期末质量调研)在△ 中, , , 分别是角 , , 的对边,且 . (1)求角 的大小; (2)若 , ,求 和 的值. 10、(奉贤区 2017 届高三上学期期末) 一艘轮船在江中向正东方向航行,在点 观测到灯 塔 在一直线上,并与航线成角 .轮船沿航线前进 米到达 处,此 时 观 测 到 灯 塔 在 北 偏 西 方 向 , 灯 塔 在 北 偏 东 方 向 , .求 .(结果用 的表达式表示). 参考答案: 一、填空、选择题 1、解析:y= ,T= ,所以,a=1 P A B, C A 45° B CB 23 cos sin( ) cos 1 x xf x x −= 0, 2x π ∈ ( )f x ABC∆ , ,A B C , ,a b c ( ) 3, 4, 52 Af a b c= = + = ABC∆ ABC a b c A B C 72cos22sin8 2 =−+ ACB A 3=a 3=+ cb b c α ( )0900 << α b β ( )0900 << α 0 00 90α β< + < , ,bα β 2 2cos sin cos2x x x− = aπ π= 2、 3、0 4、 5、 6、D 7、 8、【解析】∵ , , ∴cosα= , ∴tanα= , ∴cot2α= = . 故答案是: . 9、B 10、 11、1 12、【解析】∵ ( ), ∴T= =π,∴ω=2.故答案是:2. 13、B 14、 15、A 16. 17. 二、解答题 1、解:(1)因为 , , 所以 ....................................2 分 由余弦定理,得 ,..........5 分 所以船的行驶速度为 (海里/小时)..................6 分 (2)如图所示,以 为原点建立平面直角坐标系,设点 的坐标分别是 , 8 33 2 2− π π 22 παπ <<− 5 3sin =α 4 5 3 4 1 tan 2α 7 24 7 24 π −= 3sin πωxy 0>ω 2 | π ω| 10 2 2 π 5 12 − 0 90θ° < < ° 26sin 26 θ = 2 5 26cos 1 sin 26 θ θ= − = 2 2 2 cos 10 5BC AB AC AB AC θ= + − ⋅ = 10 5 15 52 3 = A B C, 1 1 2 2B x y C x y( , ), ( , ) 由题意,得 ............................8 分 ..................................10 分 所以直线 的方程为 .........................12 分 因为点 到直线 的距离 所以船会进入警戒水域...............................14 分 2、解:(1)依题意,在 中, ,由余弦定理得 所以 即此时该外国船只与 岛的距离为 海里.…………………………5 分 (2)过点 作 于点 在 中, ,所以 …………………… 7 分 以 为圆心, 为半径的圆交 于点 ,连结 、 , 在 中, ,所以 又 所 以 , 所 以 ……………… 11 分 外国船只到达点 的时间 (小时) 所以海监船的速度 (海里 小时) 又 , 故海监船的航向为北偏东 ,速度的最小值为 海里 小时. ……………… 1 1 cos45 40 sin 45 40 x AB y AB = ⋅ ° = = ⋅ ° = 2 2 cos(45 ) 30 sin(45 ) 20 x AC y AC θ θ = ⋅ °− = = ⋅ °− = BC 2 40 0x y− − = 0 55E −( , ) BC 0 0 2 2 | | 3 5 7ax by cd a b + += = < + ABD∆ 60DAB∠ = 2 2 2 2 22 cos60 18 20 2 18 15 cos60 364DB AD AB AD AB= + − = + − × × × = 2 91DB = D 2 91 B BC AD⊥ C Rt ABC∆ 10AC = 8CD AD AC= − = D 12 BC E AE DE Rt DEC∆ 2 2 4 5CE ED CD= − = 10 3 4 5BE = − 2 2 6 5AE AC CE= + = 4 5 2sin 36 5 CEEAC AE ∠ = = = 2arcsin 41.813EAC∠ = ≈ E 5 3 2 5 2.094 2 BEt −= = ≈ 6 5 6.4 5 3 2 5 2 AEv t ≥ = ≈ − / 90 41.81 48.2− = 48.2 6.4 / 14 分 (2)另解:建立以点 为坐标原点, 为 轴,过点 往正北作垂直的 轴。 则 , , ,设经过 小时外国船到达点 , 又 ,得 ,此时 (小时) 则 ,所以监测船的航向东偏北 所以海监船的速度 (海里 小时) 3 、 解 : ( 1 ) 设 是 中 点 , 连 , 由 , 可 知 , , , ,又 , , ,可得△ ≌△ , 故 ,可知 , …………2 分 又 , ,所以 ,故 ,在△ 中,有 , 可得 ………5 分 所以 ………8 分 (2) ……………10 分 A AD x A y (0,0)A (18,0)D (10,10 3)B t (10,10 3 4 )E t− 12ED = (10,4 5)E 10 3 4 5 2.094t −= ≈ 4 5 2 5tan 10 5 EHEAD AH ∠ = = = 2 5arctan 41.815EAD∠ = ≈ 41.81 6 5 6.4 10 3 4 5 4 AEv t ≥ = ≈ − / M CD OM OC OD= OM CD⊥ COM DOM∠ = ∠ = 1 2 COD θ∠ = sinMD R θ= OE OF= EC FD= OC OD= CEO DFO EOC DOF∠ = ∠ 1 2 4AOM BOM AOB π∠ = ∠ = ∠ = DF CD⊥ OM CD⊥ / /MO DF DFO∠ 3 4 π= DFO sin sin DF DO DOF DFO =∠ ∠ sin( )4 (cos sin )3sin 4 R DF R π θ θ θπ − = = − 2COD ODF OCE COD ODFS S S S S S∆ ∆= + + = + 21 sin 2 sin ( cos sin )2 R R R Rθ θ θ θ= + − 2 2 2sin 2 sin (0 )4R R πθ θ θ= − < < 2 2 2 21 1 1sin 2 (1 cos2 ) (sin 2 cos2 )2 2 2S R R R Rθ θ θ θ= − − = + − (其中 ) ……………………12 分 当 ,即 时, 取最大值 1. 又 ,所以 的最大值为 . ……………14 分 4、解:(1)如图建立直角坐标系, ……………………………1 分 则城市 ,当前台风中心 , 设 t 小时后台风中心 P 的坐标为 ,则 ,此时台风的半径为 , 10 小时后, km,台风的半径为 160km, , ……………………………5 分 故,10 小时后,该台风还没有开始侵袭城市 A. ………1 分 (2)因此,t 小时后台风侵袭的范围可视为以 为圆心, 为半径的圆, 若城市 A 受到台风侵袭,则 ,即 ,……………………………5 分 解得 ……………………………1 分 答:该城市受台风侵袭的持续时间为 12 小时. ……………………………1 分 5、解:(1)∵ ,∴ ……………………………2 分 由余弦定理得 ……………………………………4 分 ∴ ……………………………………….7 分 (2)∵ …………………10 分 又∵ ……………………………12 分 ∴ , 2 25 1sin(2 )2 2R Rθ ϕ= + − 1arctan 2 ϕ = 2 2 πθ ϕ+ = 4 2 π ϕθ = − sin(2 )θ ϕ+ 4 2 π ϕ− π(0, )4 ∈ S 25 1 2 R − ( )0,0A ( )30 2, 210 2P − ( ),x y 30 2 10 2 210 2 10 2 x t y t = − = − + 60 10t+ 4.184PA ≈ =r PA查看更多
相关文章
- 当前文档收益归属上传用户