2019-2020学年四川省成都市高二上学期期末调研考试（1月） 数学（理） word版

2019-2020学年四川省成都市高二上学期期末调研考试（1月） 数学（理） word版

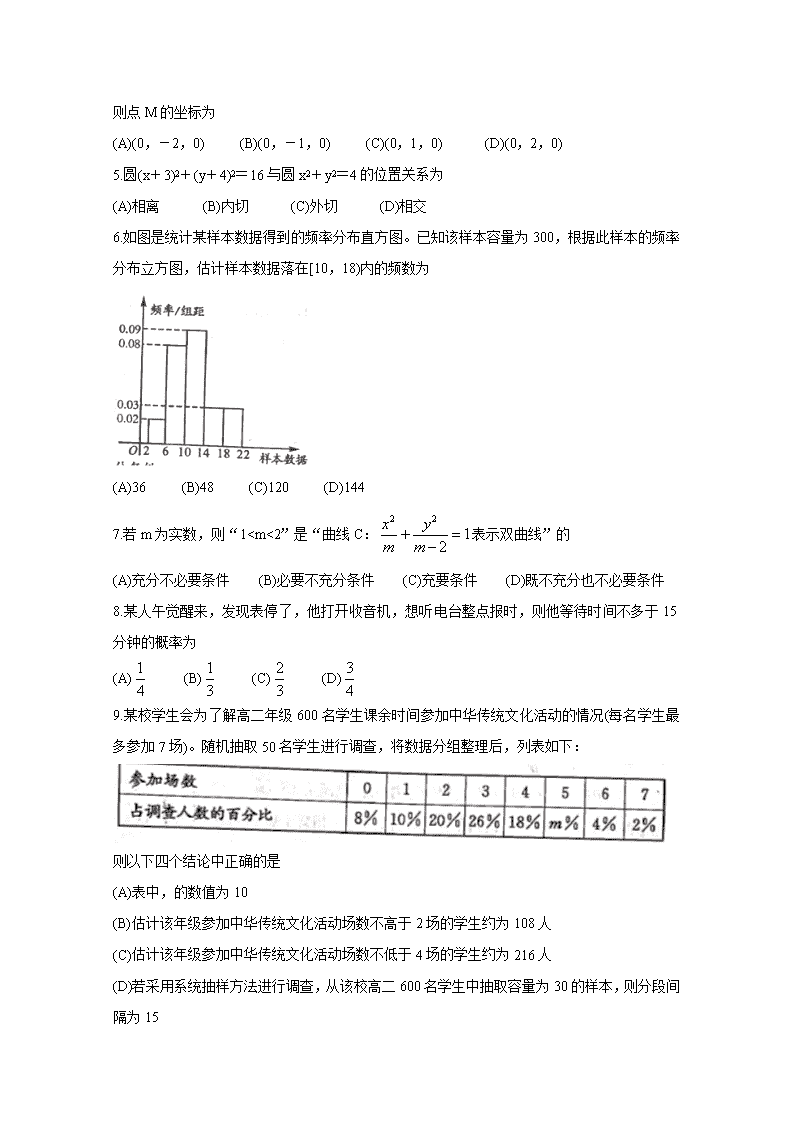
‎2019－2020学年度上期期末高二年级调研考试 数学(理科)‎ 本试卷选择题和非选择题两部分。第I卷(选择题)1至3页，第II卷(非选择题)3至4页，共4页，满分150分，考试时间120分钟。‎ 注意事项：‎ ‎1.答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。‎ ‎2.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。‎ ‎3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。‎ ‎4.所有题目必须在答题卡上作答，在试题卷上答题无效。‎ ‎5.考试结束后，只将答题卡交回。‎ 第I卷(选择题，共60分)‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.某同学在7天内每天阅读课外书籍的时间(单位：分钟)用茎叶图表示如图所示，图中左列表示时间的十位数，右列表示时间的个位数。则该同学这7天每天阅读课外书籍的时间(单位：分钟)的中位数为，：‎ ‎(A)72 (B)74 (C)75 (D)76‎ ‎2.命题“”的否定是 ‎(A) (B)‎ ‎(C) (D)‎ ‎3.双曲线的渐近线方程为 ‎(A) (B) (C) (D)‎ ‎4.在空间直角坐标系Oxyz中，y轴上一点M到点P(1，0，2)和点Q(1，－3，1)的距离相等，‎ 则点M的坐标为 ‎(A)(0，－2，0) (B)(0，－1，0) (C)(0，1，0) (D)(0，2，0)‎ ‎5.圆(x＋3)2＋(y＋4)2＝16与圆x2＋y2＝4的位置关系为 ‎(A)相离 (B)内切 (C)外切 (D)相交 ‎6.如图是统计某样本数据得到的频率分布直方图。已知该样本容量为300，根据此样本的频率分布立方图，估计样本数据落在[10，18)内的频数为 ‎(A)36 (B)48 (C)120 (D)144‎ ‎7.若m为实数，则“10，b>0)的左，右焦点分别为F1，F2，点P在双曲线C的右支上，且|PF1|＝5a，点Q是△PF1F2内一点，且满足，(S表示三角形的面积)，∠F1PF2的角平分线与直线x＝a相交于点M，且，(∈R)，则双曲线C的离心率为 。‎ 三、解答题：本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。‎ ‎17.(本小题满分10分)‎ 一个不透明的箱子中装有大小形状相同的5个小球，其中2个白球标号分别为A1，A2，3个红球标号分别为B1，B2，B3，现从箱子中随机地一次取出两个球。‎ ‎(I)求取出的两个球都是白球的概率；‎ ‎(II)求取出的两个球至少有一个是白球的概率。‎ ‎18.(本小题满分12分)‎ 已知动点P到点M(－3，0)的距离是点P到坐标原点O的距离的2倍，记动点P的轨迹为曲线C。‎ ‎(I)求曲线C的方程；‎ ‎(II)若直线x－y＋1＝0与曲线C相交于A，B两点，求|AB|的值。‎ ‎19.(本小题满分12分)‎ 已知椭圆C：(a>b>0)的左，右焦点分别为F1，F2，|F1F2|＝2，经过点F1的直线(不与x轴重合)与椭圆C相交于A，B两点，△ABF2的周长为8。‎ ‎(I)求椭圆C的方程；‎ ‎(II)经过椭圆C上的一点Q作斜率为k1，k2(k1≠0，k2≠0)的两条直线分别与椭圆C相交于异于Q点的M，N两点。若M，N关于坐标原点对称，求k1k2的值。‎ ‎20.(本小题满分12分)‎ 某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分，不低于85分称优秀)人数之间的关系进行分析研究，他们从本校初二，初二，高一，高二，高三年级各随机抽取了40名学生，记录并整理了这些学生周平均体育锻炼小时数体育成绩优秀人数，得到如下数据表：‎ 该兴趣小组确定的研究方案是：先从这5组数据中选取3组数据求线性回归方程，再用剩下的2组数据进行检验。‎ ‎(I)若选取的是初三，高一，高二的3组数据，请根据这3组数据，求出y关于x的线性回归方程；‎ ‎(II)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1，则认为得到的线性回归方程是可靠的，试问(I)中所得到的线性回归方程是否可靠?‎ 参考数据：。‎ 参考公式：。‎ ‎21.(本小题满分12分)‎ 己知动圆M与直线x＝－2相切，且与圆(x－3)2＋y2＝1外切，记动圆M的圆心轨迹为曲线C。‎ ‎(I)求曲线C的方程；‎ ‎(II)若直线l与曲线C相交于A，B：两点，且(O为坐标原点)，证明直线l经过定点H，并求出H点的坐标。‎ ‎22.(本小题满分12分)‎ 在平面直角坐标系中，以坐标原点为中心，以坐标轴为对称轴的椭圆C经过点M(2，1)，N(，－)。‎ ‎(I)求椭圆C的标准方程；‎ ‎(II)经过点M作倾斜角互补的两条直线，分别与椭圆C相交于异于M点的A，B两点，当△AMB面积取得最大值时，求直线AB的方程。‎