- 2021-06-15 发布 |
- 37.5 KB |
- 8页
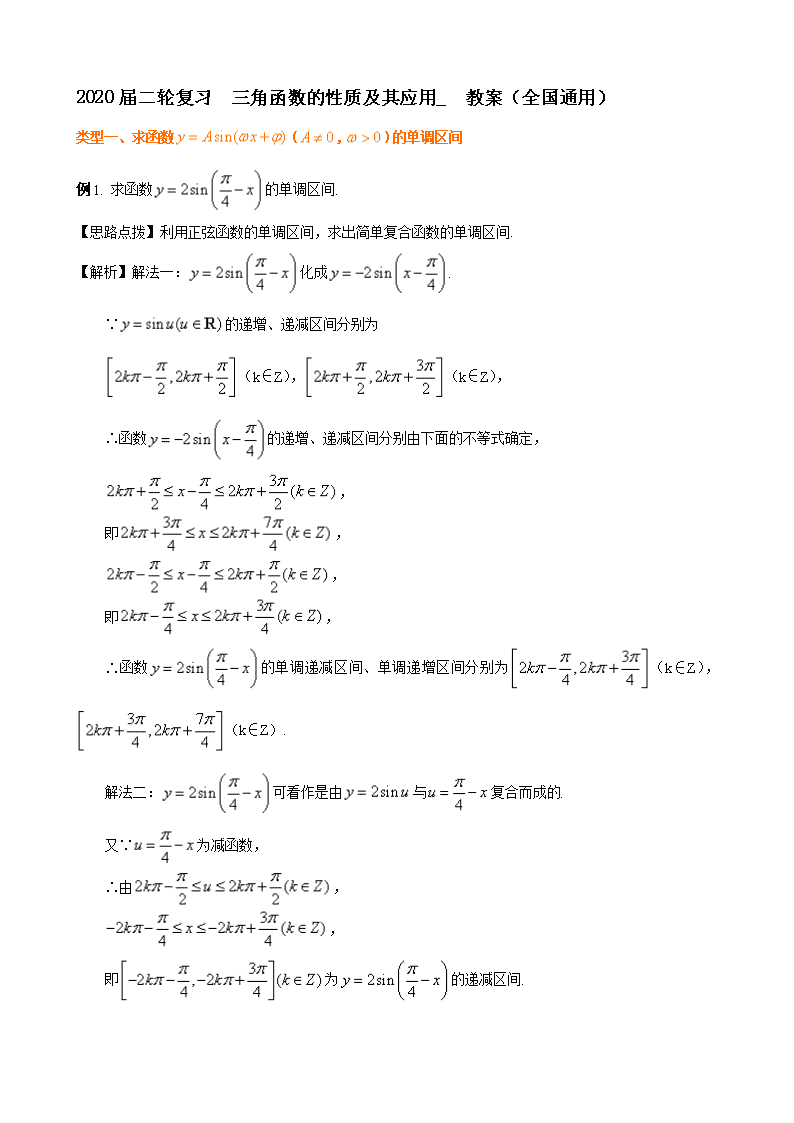


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习三角函数的性质及其应用教案(全国通用)
2020届二轮复习 三角函数的性质及其应用_ 教案(全国通用) 类型一、求函数(,)的单调区间 例1. 求函数的单调区间. 【思路点拨】利用正弦函数的单调区间,求出简单复合函数的单调区间. 【解析】解法一:化成. ∵的递增、递减区间分别为 (k∈Z),(k∈Z), ∴函数的递增、递减区间分别由下面的不等式确定, , 即, , 即, ∴函数的单调递减区间、单调递增区间分别为(k∈Z),(k∈Z). 解法二:可看作是由与复合而成的. 又∵为减函数, ∴由, , 即为的递减区间. 由, 即得 , 即为的递增区间。 综上可知:的递增区间为; 递减区间为. 【总结升华】熟练掌握函数的单调区间的确定的两种方法.三角函数单调区间的确定,一般先将函数式化为基本三角函数的标准式,然后通过同解变形或利用数形结合的方法来求解. 举一反三: 【变式1】求下列函数的单调递增区间. (1),(2),(3). 【解析】 (1)∵,∴递增区间为:(); (2)画出的图象: 可知增区间为(); (3)函数在区间()上是增函数. 【变式2】利用单调性比较,,的大小: 【解析】 ∵,,且 ∴ 类型二、三角函数的图象及其变换 例2.已知函数 (1)用五点法作出它的图象; (2)指出这个函数的振幅、周期、频率、初相和单调区间; (3)说明该函数的图象可由的图象经过怎样的变换而得到? 【思路点拨】化简,令,分别求出对应的值,再描点作图,注意图象变换的时候每一个变换总是对字母而言的. 【解析】(1). 列表描点绘图如下: (2)如图可知,此函数的振幅是2,周期为,频率为,初相为. 单调增区间为 kÎZ , 单调减区间为kÎZ. (3)法一: 法二: 【总结升华】 ①五点法作(,)的简图时,五点取法是设,由取0、、 、、来求相应的值及对应的值,再描点作图; ②由的图象变换出的图象一般先平移后伸缩,但先伸缩后平移也经常出现,无论哪种变形,请切记每一个变换总是对字母而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少; ③此处的难点是函数图象的平移,可以选择画出图象后观察;也可以直接由函数式子利用特殊位置点(如:首点、波峰、波谷等)的坐标判定,但其前提是两个函数的名称以及的系数是相同的. 举一反三: 【变式1】由的图象得到的图象需要向 平移 个单位. 【答案】左,; 【解析】∵, ∴由的图象得到的图象需要向左平移个单位. 【变式2】试述如何由的图象得到的图象. 【解析】方法一: . 方法二: . 【变式3】若函数的图象上的每个点的纵坐标不变,将横坐标缩小为原来的,再将图象沿轴向右平移个单位,则新图象对应的函数式是( ) A. B. C. D. 【答案】A 【变式4】画出函数在区间上的图象. 【解析】由知道: x 0 y -1 0 1 0 故函数在区间上的图象: 例3. 如图,它是函数的图象,由图中条件,写出该函数的解析式。 【思路点拨】结合图形易求得A,及.如何求呢?可以选择点的坐标代入函数解析式尝试一下,结合的范围求得. 【解析】 由图知A=5, 由,得 ∴。此时。 下面介绍怎样求初相。 解法一:(单调性法) ∵点(π,0)在递减的那段曲线上, ∴。 由得, ∴。 ∵,∴。 解法二:(最值点法) 将最高点坐标代入,得, ∴,∴。 又,∴。 解法三:(起始点法) 函数的图象一般由“五点法”作出,而起始点的横坐标x正是由解得的。故只要找出起始点横坐标x0,就可以迅速求得角。由图象易得, ∴。 解法四:(平移法) 由图象知,将的图象沿x轴向左平移个单位就得到本题图象,故所求函数解析式为 【总结升华】给出型的图象,求它的解析式,常从寻找“五点法”中的第一个零点作为突破口,要从图象的升降找准第一个零点的位置,例3中的解法三是我们常选用的方法这一. 举一反三: 【变式】下图是函数(,)的图象.则、的值是( ) A., B., C., D., 【答案】C 【解析】由图象可得: ∵,由得, 由 ,得 ∴ () 由,得.满足时,或. 由此得到,.注意到,即, 因此,这样就排除了. ∴, 注意:因为函数是周期函数,所以仅靠图像上的三个点,不能完全确定A、、的值.本题虽然给出了,的条件,但是仅靠(0,1 )、两点,不能完全确定、的值.在确定的过程中,比较隐蔽的条件()起了重要作用. 类型三:奇偶性与对称性 例4.已知函数 (1)判断函数的奇偶性;(2)判断函数的对称性。 【思路点拨】正弦函数的定义域是,在考查与的关系;考查三角函数的对称性的时候,从对称轴和对称中心两个方面考虑. 【解析】(1)的定义域关于原点对称, ∵且, ∴函数不是奇函数也不是偶函数. (2)∵令,则的图象的对称轴是,对称中心(), ∴函数的图象的对称轴是即() 由得(), ∴函数的图象的对称中心是(). 【总结升华】①先求定义域并判断在数轴上关于原点对称,再经过等值变形尽量转化为一个角的一个三角函数式(),再判断其奇偶性.函数的奇偶性与函数的对称性既有联系又有区别,用定义法,换元法。 ②对于()来说,对称中心与零点(平衡位置)相联系,对称轴与最值点(极值点)联系. 举一反三: 【变式1】判断下列函数的奇偶性 (1); (2). 【解析】 (1)定义域关于原点对称, 又 ∴ 函数为奇函数。 (2)∵从分母可以得出(),∴定义域在数轴上关于原点不对称。 ∴ 函数为非奇非偶函数 【变式2】设函数的图象的一条对称轴方程是( ) A. B. C. D. 【答案】A查看更多