- 2021-06-15 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012年文数高考试题答案及解析-广东
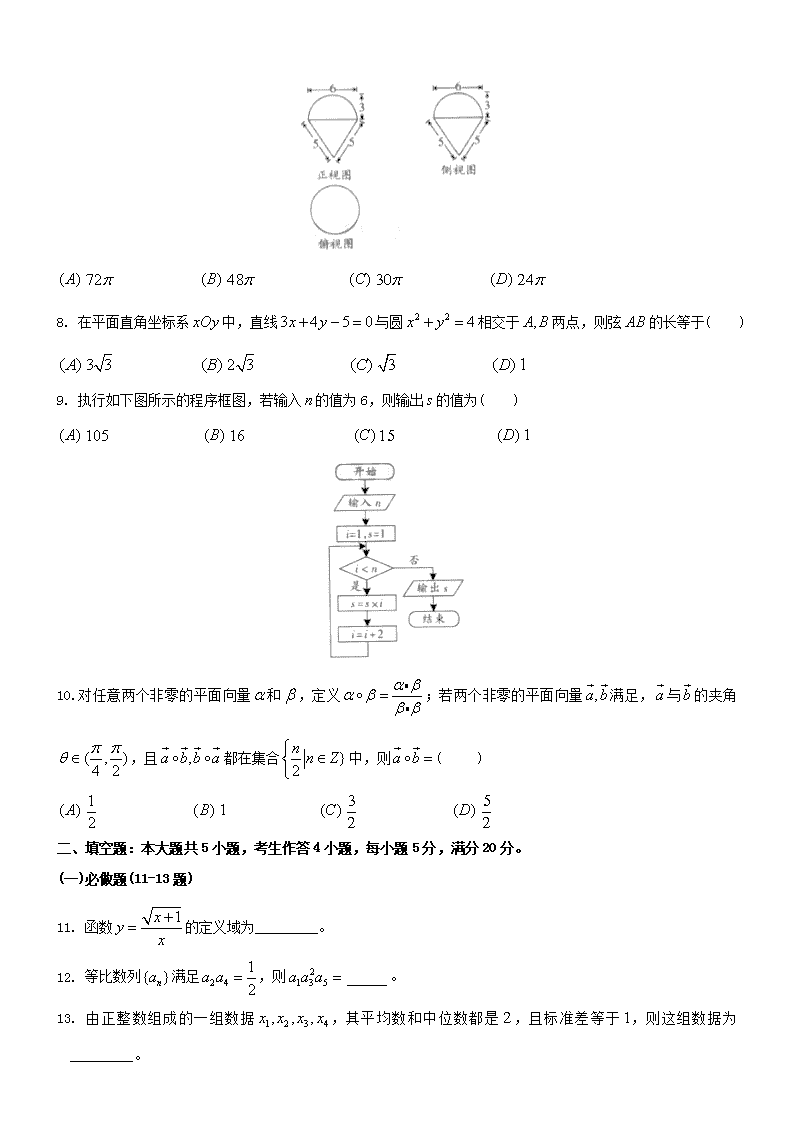
2012 年普通高等学校招生全国统一考试(广东卷)数学(文科) 本试题共 4 页,21 小题,满分 150 分,考试用时 120 分钟。 参考公式: 锥体的体积公式 1 3 V Sh ,其中 S为柱体的底面积, h为柱体的高. 球的体积 34 3 V R ,其中 R为球的半径。 一组数据 1 2, , , nx x x 的标准差 2 2 2 1 2 1 [( ) ( ) ( ) ]ns x x x x x x n ,其中 x表示这组数据的平均数。 一、选择题:本大题共 10 小题,每小题 5 分,满分 40 分,在每小题给出四个选项中,只有一项符合题目要求。 1. 设 i为虚数单位,则复数 3 4i i =( ) ( )A 4 3i ( )B 4 3i ( )C i ( )D i 2.设集合 {1,2,3,4,5,6}, {1,3,5}U M ;则 UC M ( ) ( )A { , , } ( )B {1,3,5} ( )C { , , } ( )D U 3. 若向量 (1, 2), (3, 4)AB BC ;则 AC ( ) ( )A (4,6) ( )B ( 4, 6) ( )C ( , ) ( )D ( , ) 4. 下列函数为偶函数的是( ) ( )A siny x ( )B 3y x ( )C xy e ( )D lny x 5. 已知变量 ,x y满足约束条件 1 1 0 1 x y x x y ,则 2z x y 的最小值为( ) ( )A 3 ( )B 1 ( )C 5 ( )D 6 6. 在 ABC 中,若 60 , 45 , 3 2A B BC ,则 AC ( ) ( )A 4 3 ( )B 2 3 ( )C ( )D 7.某几何体的三视图如图 1 所示,它的体积为( ) ( )A 72 ( )B 48 ( )C ( )D 8. 在平面直角坐标系 xOy中,直线3 4 5 0x y 与圆 2 2 4x y 相交于 ,A B两点,则弦 AB的长等于( ) ( )A 3 3 ( )B 2 3 ( )C ( )D 9. 执行如下图所示的程序框图,若输入 n的值为 6,则输出 s的值为( ) ( )A 105 ( )B 16 ( )C ( )D 10.对任意两个非零的平面向量 和 ,定义 ;若两个非零的平面向量 ,a b 满足, a 与 b 的夹角 ( , ) 4 2 ,且 ,a b b a 都在集合 } 2 n n Z 中,则 a b ( ) ( )A 1 2 ( )B 1 ( )C ( )D 二、填空题:本大题共 5 小题,考生作答 4 小题,每小题 5 分,满分 20 分。 (一)必做题(11-13 题) 11. 函数 1xy x 的定义域为_________。 12. 等比数列{ }na 满足 2 4 1 2 a a ,则 2 1 3 5a a a _____。 13. 由正整数组成的一组数据 1 2 3 4, , ,x x x x ,其平均数和中位数都是 2,且标准差等于1,则这组数据为_________。 (从小到大排列) (二)选做题(14 - 15 题,考生只能从中选做一题) 14. (坐标系与参数方程选做题) 在平面直角坐标系 xOy中,曲线 1C 和 2C 的参数方程分别为 2 5 cos : 5 sin x C y ( 是参数,0 2 )和 2 21 2: 2 2 x t C y t ( t是参数),它们的交点坐标为_______. 15.(几何证明选讲选做题)如图3所示,直线 PB与圆O想切于点 B,D是弦 AC上的点, PBA DBA , 若 ,AD m AC n ,则 AB _______。 三、解答题:本大题共 6 小题,满分 80 分。解答需写出文字说明、证明过程和演算步骤。 16. (本小题满分 12 分)已知函数 ( ) cos( )( ) 4 6 xf x A x R ,且 ( ) 2 3 f 。 (1)求 A的值;(2)设 , [0, ] 2 , 4 30 2 8(4 ) , (4 ) 3 17 3 5 f f ;求 cos( ) 的值 17.(本小题满分 13 分)某校 100 名学生期中考试语文成绩的频率分布直方图如图 4 所示,其中成绩分组区间是: [50,60][60,70][70,80][80,90][90,100]。 (1)求图中a的值; (2)根据频率分布直方图,估计这 100 名学生语文成绩的平均分; (3)若这 100 名学生语文成绩某些分数段的人数( x )与数学成绩相应分数段的人数( y )之比如下表所示,求数学 成绩在[50,90)之外的人数。 18.(本小题满分 13 分)如下图 5所示,在四棱锥 P ABCD 中,AB 平面PAD, / / ,AB CD PD AD ,E是 PB中点,F 是DC 上的点,且 1 2 DF AB ,PH 为 PAD 中 AD边上的高。 (1)证明:PH 平面 ABCD; (2)若 1, 2, 1PH AD FC ,求三棱锥 E BCF 的体积; (3)证明:EF 平面 PAB. 19.(本小题满分 14 分)设数列 na 的前 n项和为 nS ,数列 nS 的前 n项和为 nT ,满足 2 *2n nT S n n N , . (1)求 1a 的值;(2)求数列 na 的通项公式。 20.(本小题满分 14 分)在平面直角坐标系 xoy中,已知椭圆 2 2 1 2 2: 1 ( 0)x yC a b a b 的左焦点为 1( 1 0)F , , 且点 (0 1)P , 在 1C 上。(1)求 1C 的方程;(2)设直线 l同时与椭圆 1C 和抛物线 2 2 : 4C y x 相切,求直线 l的方程。 21.(本小题满分 14 分)设0 1a ,集合 { | 0}A x R x , 2{ | 2 3(1 ) 6 0}B x R x a x a , D A B 。(1)求集合D (用区间表示);(2)求函数 3 2( ) 2 3(1 ) 6f x x a x ax 在D内的极值点。 2012 年普通高等学校招生全国统一考试(广东卷)数学(文科)参考答案 一、选择题:本大题共 10 小题,每小题 5 分,满分 40 分。 1 2 3 4 5 6 7 8 9 10 D A A D C B C B C A 1. 【解析】选D 依题意: 2 3 4 (3 4 ) 4 3i i i i i i 2.【解析】选 A UC M { , , } 3. 【解析】选 A (4,6)AC AB BC 4. 【解析】选D siny x 与 3y x 是奇函数,, xy e 是非奇非偶函数 5. 【解析】选C 约束条件对应 ABC 边际及内的区域: (1,0), ( 1, 2), 1, 2)A B C ,则 2 [ 5,3]z x y 6. 【解析】选B 由正弦定理得: 3 2 2 3 sin sin sin 60 sin 45 BC AC AC AC A B 7.【解析】选C 几何体是半球与圆锥叠加而成,它的体积为 3 2 2 21 4 13 3 5 3 30 2 3 3 V 8. 【解析】选B 圆 2 2 4x y 的圆心 (0,0)O 到直线3 4 5 0x y 的距离 5 1 5 d ,弦 AB的长 2 22 2 3AB r d 9. 【解析】选C s 1 1 3 15 i 1 3 5 7 10. 【解析】选 A 2 1cos 0, cos 0 ( ) ( ) cos (0, ) 2 a b a b b a a b b a b a ,a b b a 都在集合 } 2 n n Z 中得: *1 2 1 2 1( ) ( ) ( , ) 4 2 n na b b a n n N a b 。 二、填空题:本大题共 5 小题,考生作答 4 小题,每小题 5 分,满分 20 分。 (一)必做题(11-13 题) 9. 【解析】定义域为[ 1,0) (0, ) , 1xy x 中的 x满足: 1 0 1 0 0 x x x 或 0x 10. 【解析】 2 1 3 5a a a 1 4 , 2 2 4 2 4 3 1 3 5 3 1 1 1, 2 2 4 a a a a a a a 11. 【解析】这组数据为1,1,3,3,不妨设 1 2 3 4x x x x 得: 2 3 1 2 3 4 1 44, 8 4x x x x x x x x 2 2 2 2 2 1 2 3 41 ( 2) ( 2) ( 2) ( 2) 4 2 0,1,2is x x x x x ①如果有一个数为0或 4;则其余数为 2,不合题意;②只能取 2 1ix ;得:这组数据为1,1,3,3 (二)选做题(14 - 15 题,考生只能从中选做一题) 14.【解析】它们的交点坐标为 (2,1), 2 2 1 2: 5( , 0), : 1C x y x y C y x 解得:交点坐标为 (2,1) 15.【解析】 AB mn , ,PBA DBA ACB BAD CAB BAD CAB 得: 2AB AD AB AC AD mn AB mn AC AB 。 三、解答题:本大题共 6 小题,满分 80 分。解答需写出文字说明、证明过程和演算步骤。 16.解:(1) ( ) 2 cos 2 2 3 4 f A A 。 (2) 4 30 15 15(4 ) cos( ) sin 3 17 2 17 17 f , [0, ] 2 , 8cos 17 。 2 8 4(4 ) cos 3 5 5 f , [0, ] 2 , 3sin 5 , 4 8 3 15 13cos( ) cos cos sin sin 5 17 5 17 85 17.解:(1) (2 0.02 0.03 0.04) 10 1 0.005a a 。 (2)平均分为55 0.05 65 0.4 75 0.3 85 0.2 95 0.05 73 。 (3)数学成绩在 [50,90) 内的人数为 1 4 5(0.005 0.04 0.03 0.02) 10 100 90 2 3 4 人,数学成绩在 [50,90)外的人数为100 90 10 人。 答:(1) 0.005a ;(2)这 100 名学生语文成绩的平均分为73;(3)数学成绩在[50,90)外的人数为10人。 18.(1)证明: AB 平面 PAD,PH 面 PAD PH AB ,又 ,PH AD AD AB 、 平面 ABCD, AD AB A PH 平面 ABCD。 (2)E是PB中点点 E到面 BCF 的距离 1 1 2 2 h PH , 三棱锥 E BCF 的体积 1 1 1 1 1 21 2 3 3 2 6 2 12BCFV S h FC AD h 。 (3)取PA的中点为G,连接 ,DG EG。 PD AD DG PA ,又 AB 平面 PAD, AB 平面 PAB平面 PAD 平面 PAB, 又平面 PAD平面 PAB PA ,DG 平面 PAD DG 面 PAB, 点 ,E G是棱 ,PB PA的中点 1/ / 2 EG AB ,又 1/ / / / / / 2 DF AB EG DF DG EF ,得:EF 平面 PAB。 19.解:(1)在 2 *2n nT S n n N , 中,令 1 1 1 1 11 2 1 2 1 1n T S a a a 。 (2) 2 2 1 12 2 ( 1)n n n nT S n T S n , ,相减得: 1 2 (2 1)n nS S n , 2 12 (2 3)n nS S n , 相减得: 2 12 2n na a , 1 2 1 21 2 3 4a S S a , 2 12 2a a ,得 1 2 2n na a , 1 12 2 2 2( 2)n n n na a a a ,得:数列{ 2}na 是以 1 2 3a 为首项, 2为公比的等比数列, 1 12 3 2 3 2 2n n n na a 。 20.解:(1)由题意得: 2 21, 1 2b c a b c ,故椭圆 1C 的方程为: 2 2 1 2 x y 。 (2)①当直线 l的斜率不存在时,设直线 :l x m ,直线 l与椭圆 1C 相切 2m ,直线与抛物线 2 2 : 4C y x 相切 0m ,得:m不存在。 ②当直线 l的斜率存在时,设直线 :l y kx m ,直线 l与椭圆 1C 相切 2 2 2(1 2 ) 4 2 2 0k x kmx m 两根 相等 2 2 1 0 2 1m k ;直线与抛物线 2 2 : 4C y x 相切 2 2 22( 2) 0k x km x m 两根相等 2 0 1km ,解得: 2 , 2 2 k m 或 2 2, 2 : ( 2) 2 2 k m l y x 。 21.解:(1)对于方程 22 3(1 ) 6 0x a x a ,判别式 29(1 ) 48 3( 3)(3 1)a a a a 。 因为0 1a ,所以 3 0a 。 当 1 1 3 a 时, 0 ,此时B R ,所以 0,D A ; 当 1 3 a 时, 0 ,此时 { | 1}B x x ,所以 (0,1) (1, )D ; 当 10 3 a 时, 0 ,设方程 22 3(1 ) 6 0x a x a 的两根为 1 2,x x 且 1 2x x , 则 1 3(1 ) 3( 3)(3 1) 4 a a a x , 2 3(1 ) 3( 3)(3 1) 4 a a a x , 1 2{ | }B x x x x x 或 1 2 3 (1 ) 0 2 x x a , 1 2 3 0x x a ,所以 1 20, 0x x ,此时, 1 2(0, ) ( , )D x x 3(1 ) 3( 3)(3 1) 3(1 ) 3( 3)(3 1) (0, ) ( , ) 4 4 a a a a a a 综上可知,当 10 3 a 时, 3(1 ) 3( 3)(3 1) 3(1 ) 3( 3)(3 1) (0, ) ( , ) 4 4 a a a a a a D ; 当 1 3 a 时, (0,1) (1, )D ;当 1 1 3 a 时, 0,D 。 (2) 2( ) 6 6(1 ) 6 6( 1)( )f x x a x a x x a (0 1)a ,由 ( ) 0 1f x a x , 由 ( ) 0f x x a 或 1x ,所以函数 ( )f x 在区间 ,a 和 1, 上为递增,在区间 ,1a 上为递减。 当 1 1 3 a 时,因为 0,D ,所以 ( )f x 在D内有极大值点 a和极小值点1; 当 1 3 a 时, (0,1) (1, )D ,所以 ( )f x 在D内有极大值点 1 3 a ; 当 10 3 a 时, 3(1 ) 3( 3)(3 1) 3(1 ) 3( 3)(3 1) (0, ) ( , ) 4 4 a a a a a a D 3(1 ) 3( 3)(3 1) 3(1 ) 3( 3)(3 1) 1 4 4 a a a a a a a , ( )f x 在D内有极大值点 a。 综上可知:当 10 3 a 时, ( )f x 在D内有极大值点 a;当 1 1 3 a 时, ( )f x 在D内有极大值点 a和极小值 点1。查看更多