- 2021-06-15 发布 |
- 37.5 KB |
- 21页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018年云南省玉溪市高考数学模拟试卷(11)
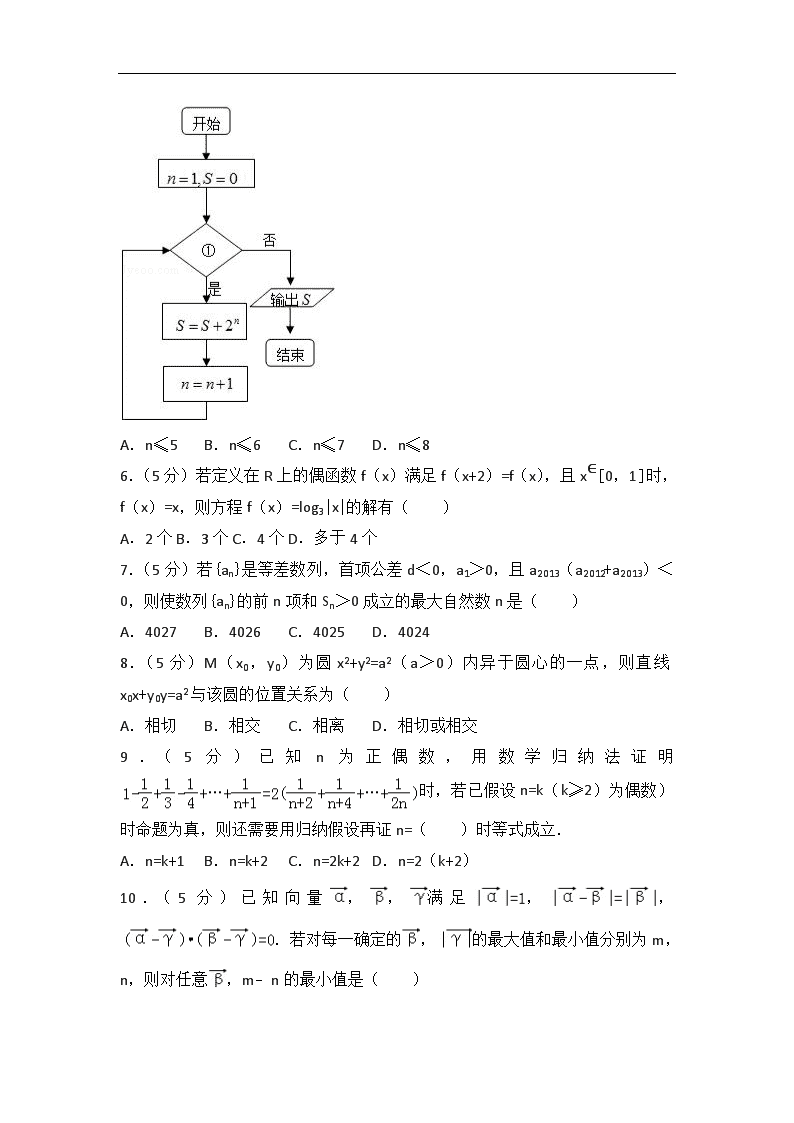
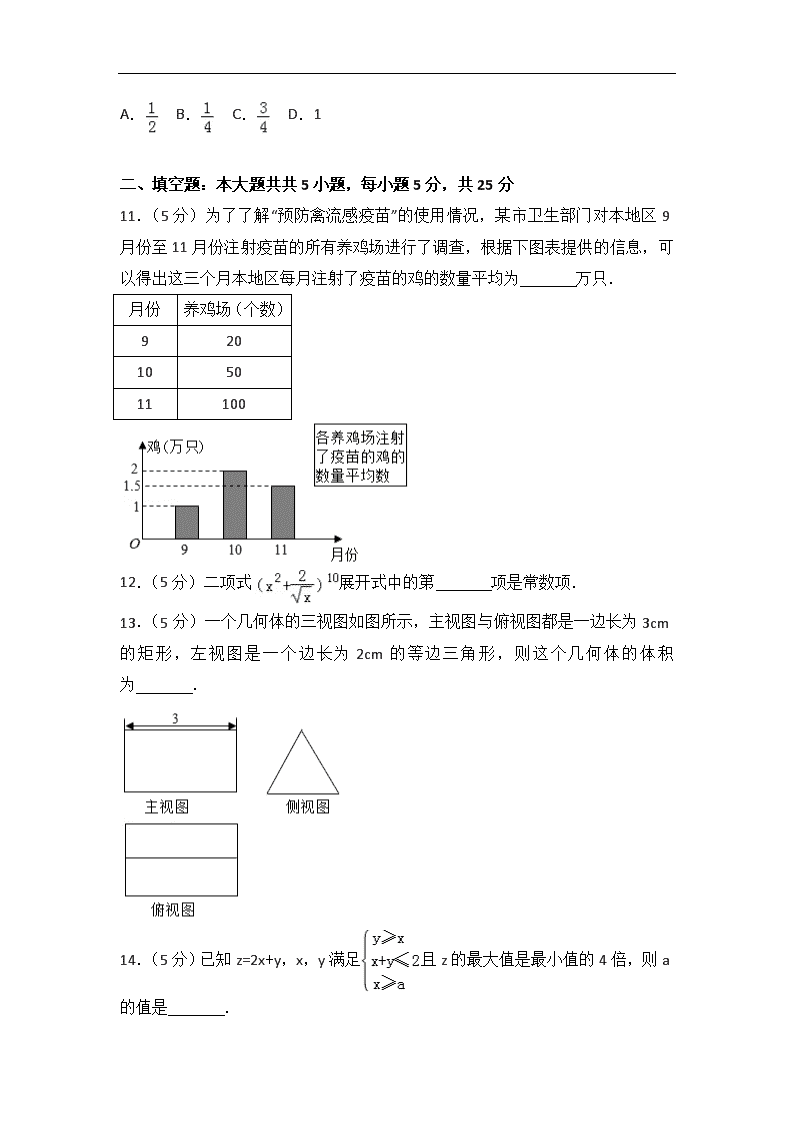
2018年云南省玉溪市高考数学模拟试卷(11) 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)若复数(a∈R,i为虚数单位)是纯虚数,则实数a的值为( ) A.6 B.﹣6 C.5 D.﹣4 2.(5分)函数的图象大致是( ) A. B. C. D. 3.(5分)设m、n是两条不同的直线,α、β、γ是三个不同的平面,给出下列四个命题: ①若α∥β,α∥γ,则β∥γ; ②若α⊥β,m∥α,则m⊥β; ③若m⊥α,m∥β,则α⊥β; ④若m∥n,n⊂α,则m∥α. 其中正确命题的序号是( ) A.①③ B.①④ C.②③ D.②④ 4.(5分)设函数f(x)=cos(2x+φ)+sin(2x+φ)(|φ|<),且图象关于直线x=0对称,则( ) A.y=f(x)的最小正周期为π,且在上为增函数 B.y=f(x)的最小正周期为π,且在上为减函数 C.y=f(x)的最小正周期为,且在上为增函数 D.y=f(x)的最小正周期为,且在上为减函数 5.(5分)若程序框图输出S的值为126,则判断框①中应填入的条件是( ) A.n≤5 B.n≤6 C.n≤7 D.n≤8 6.(5分)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的解有( ) A.2个 B.3个 C.4个 D.多于4个 7.(5分)若{an}是等差数列,首项公差d<0,a1>0,且a2013(a2012+a2013)<0,则使数列{an}的前n项和Sn>0成立的最大自然数n是( ) A.4027 B.4026 C.4025 D.4024 8.(5分)M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系为( ) A.相切 B.相交 C.相离 D.相切或相交 9.(5分)已知n为正偶数,用数学归纳法证明时,若已假设n=k(k≥2)为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立. A.n=k+1 B.n=k+2 C.n=2k+2 D.n=2(k+2) 10.(5分)已知向量,,满足,,.若对每一确定的,的最大值和最小值分别为m,n,则对任意,m﹣n的最小值是( ) A. B. C. D.1 二、填空题:本大题共共5小题,每小题5分,共25分 11.(5分)为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查,根据下图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 万只. 月份 养鸡场(个数) 9 20 10 50 11 100 12.(5分)二项式展开式中的第 项是常数项. 13.(5分)一个几何体的三视图如图所示,主视图与俯视图都是一边长为3cm的矩形,左视图是一个边长为2cm的等边三角形,则这个几何体的体积为 . 14.(5分)已知z=2x+y,x,y满足且z的最大值是最小值的4倍,则a的值是 . 15.(5分)给出如下四个结论: ①若“p且q”为假命题,则p、q均为假命题; ②命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”; ③若随机变量ζ~N(3,4),且P(ζ<2a﹣3)=P(ζ>a+2),则a=3; ④过点A(1,4),且横纵截距的绝对值相等的直线共有2条. 其中正确结论的序号是 . 三、解答题:本大题共共6小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤 16.(12分)已知函数的图象过点M(,0). (1)求m的值; (2)在△ABC中,角A,B,C的对边分别是a,b,c,若ccosB+bcosC=2acosB,求f(A)的取值范围. 17.(12分)已知函数f(x)=ex+tx(e为自然对数的底数). (Ⅰ)当t=﹣e时,求函数f(x)的单调区间; (Ⅱ)若对于任意x∈(0,2],不等式f(x)>0恒成立,求实数t的取值范围. 18.(12分)如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点. (Ⅰ)求证:AF⊥平面CDE; (Ⅱ)求面ACD和面BCE所成锐二面角的大小. 19.(12分)某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响. (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望; (Ⅱ)试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力. 20.(13分)已知F(1,0),P是平面上一动点,P到直线l:x=﹣1上的射影为点N,且满足 (Ⅰ)求点P的轨迹C的方程; (Ⅱ)过点M(1,2)作曲线C的两条弦MA,MB,设MA,MB所在直线的斜率分别为k1,k2,当k1,k2变化且满足k1+k2=﹣1时,证明直线AB恒过定点,并求出该定点坐标. 21.(14分)已知数列{an}满足:(其中常数λ>0,n∈N*). (Ⅰ)求数列{an}的通项公式; (Ⅱ)求证:当λ=4时,数列{an}中的任何三项都不可能成等比数列; (Ⅲ)设Sn为数列{an}的前n项和.求证:若任意n∈N*,(1﹣λ)Sn+λan≥3. 2018年云南省玉溪市高考数学模拟试卷(11) 参考答案与试题解析 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)若复数(a∈R,i为虚数单位)是纯虚数,则实数a的值为( ) A.6 B.﹣6 C.5 D.﹣4 【解答】解:==﹣i 根据纯虚数的概念得出 解得a=6. 故选A. 2.(5分)函数的图象大致是( ) A. B. C. D. 【解答】解:∵y=f(﹣x)==﹣f(x), ∴y=f(x)=为奇函数, ∴y=f(x)的图象关于原点成中心对称,可排除B; 又x>0时,f(x)=,f′(x)=, ∴x>e时,f′(x)<0,f(x)在(e,+∞)上单调递减, 0<x<e时,f′(x)>0,f(x)在(0,e)上单调递增,故可排除A,D,而C满足题意. 故选C. 3.(5分)设m、n是两条不同的直线,α、β、γ是三个不同的平面,给出下列四个命题: ①若α∥β,α∥γ,则β∥γ; ②若α⊥β,m∥α,则m⊥β; ③若m⊥α,m∥β,则α⊥β; ④若m∥n,n⊂α,则m∥α. 其中正确命题的序号是( ) A.①③ B.①④ C.②③ D.②④ 【解答】解:对于①,若α∥β,α∥γ根据面面平行的性质容易得到β∥γ;故①正确; 对于②,若α⊥β,m∥α,m与β的关系不确定;故②错误; 对于③,若m⊥α,m∥β,可以在β找到一条直线n与m平行,所以n⊥α,故α⊥β;故③正确; 对于④,若m∥n,n⊂α,那么m与α的位置关系为m∥α或者m⊂α;故④错误; 故选A. 4.(5分)设函数f(x)=cos(2x+φ)+sin(2x+φ)(|φ|<),且图象关于直线x=0对称,则( ) A.y=f(x)的最小正周期为π,且在上为增函数 B.y=f(x)的最小正周期为π,且在上为减函数 C.y=f(x)的最小正周期为,且在上为增函数 D.y=f(x)的最小正周期为,且在上为减函数 【解答】解:f(x)=cos(2x+φ)+sin(2x+φ) =2[cos(2x+φ)+sin(2x+φ)] =2cos(2x+φ﹣), ∵ω=2, ∴T==π, 又函数图象关于直线x=0对称, ∴φ﹣=kπ(k∈Z),即φ=kπ+(k∈Z), 又|φ|<, ∴φ=, ∴f(x)=2cos2x, 令2kπ≤2x≤2kπ+π(k∈Z),解得:kπ≤x≤kπ+(k∈Z), ∴函数的递减区间为[kπ,kπ+](k∈Z), 又(0,)⊂[kπ,kπ+](k∈Z), ∴函数在(0,)上为减函数, 则y=f(x)的最小正周期为π,且在(0,)上为减函数. 故选B 5.(5分)若程序框图输出S的值为126,则判断框①中应填入的条件是( ) A.n≤5 B.n≤6 C.n≤7 D.n≤8 【解答】解:分析程序中各变量、各语句的作用, 再根据流程图所示的顺序,可知: 该程序的作用是输出满足条件S=2+22+23+…+2n=126时S的值 ∵2+22+23+…+26=126 故最后一次进行循环时n的值为6, 故判断框中的条件应为n≤6 故选B 6.(5分)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的解有( ) A.2个 B.3个 C.4个 D.多于4个 【解答】解:解:由f(x+2)=f(x)可得函数的周期为2, 又函数为偶函数且当x∈[0,1]时,f(x)=x, 故可作出函数f(x)得图象. ∴方程f(x)=log3|x|的解个数等价于f(x)与y=log3|x|图象的交点, 由图象可得它们有4个交点,故方程f(x)=log3|x|的解个数为4, 故选:C. 7.(5分)若{an}是等差数列,首项公差d<0,a1>0,且a2013(a2012+a2013)<0,则使数列{an}的前n项和Sn>0成立的最大自然数n是( ) A.4027 B.4026 C.4025 D.4024 【解答】解:由题意可得数列{an}单调递减, 由a2013(a2012+a2013)<0可得: a2012>0,a2013<0,|a2012|>|a2013|. ∴a2012+a2013>0. 则S4025=4025a2013<0, 故使数列{an}的前n项和Sn>0成立的最大自然数n是4024. 故选D. 8.(5分)M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系为( ) A.相切 B.相交 C.相离 D.相切或相交 【解答】解:由圆的方程得到圆心坐标为(0,0),半径r=a, 由M为圆内一点得到:<a, 则圆心到已知直线的距离d=>=a=r, 所以直线与圆的位置关系为:相离. 故选C 9.(5分)已知n为正偶数,用数学归纳法证明时,若已假设n=k(k≥2)为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立. A.n=k+1 B.n=k+2 C.n=2k+2 D.n=2(k+2) 【解答】解:由数学归纳法的证明步骤可知,假设n=k(k≥2)为偶数)时命题为真, 则还需要用归纳假设再证n=k+2, 不是n=k+1,因为n是偶数,k+1是奇数, 故选B. 10.(5分)已知向量,,满足,,.若对每一确定的, 的最大值和最小值分别为m,n,则对任意,m﹣n的最小值是( ) A. B. C. D.1 【解答】解:∵, ∴令=则A必在单位圆上, 又∵又向量满足, ∴令=则点B必在线段OA的中垂线上, =. 又∵ 故C点在以线段AB为直径的圆M上,任取一点C,记=. 故m﹣n就是圆M的直径|AB| 显然,当点B在线段OA的中点时,(m﹣n)取最小值 即(m﹣n)min= 故选A 二、填空题:本大题共共5小题,每小题5分,共25分 11.(5分)为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查,根据下图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 90 万只. 月份 养鸡场(个数) 9 20 10 50 11 100 【解答】解:9月份注射疫苗的鸡的数量是20×1=20万只, 10月份注射疫苗的鸡的数量是50×2=100万只, 11月份注射疫苗的鸡的数量是100×1.5=150万只, 这三个月本地区平均每月注射了疫苗的鸡的数量为 =90(万只). 故答案为:90. 12.(5分)二项式展开式中的第 九 项是常数项. 【解答】解:二项式的通项为Tr+1=(x2)10﹣r()r=2r x, 令 =0得r=8, 故展开式中的常数项是第9项. 故答案为:九. 13.(5分)一个几何体的三视图如图所示,主视图与俯视图都是一边长为3cm的矩形,左视图是一个边长为2cm的等边三角形,则这个几何体的体积为 . 【解答】解:由三视图知几何体是一个三棱柱, ∵三棱柱的底面是一个边长为2的正三角形, 三棱柱的侧棱与底面垂直且长度是3, ∴三棱柱的体积是 ×2×2××3=3 , 故答案为:. 14.(5分)已知z=2x+y,x,y满足且z的最大值是最小值的4倍,则a的值是 . 【解答】解:由题意可得,B(1,1) ∴a<1,不等式组表示的 平面区域如图所示的△ABC 由z=2x+y可得y=﹣2x+z,则z表示直线y=﹣2x+z在y轴上的截距,截距越大,z越大 作直线L:y=﹣2x,把直线向可行域平移,当直线经过C时z最小,当直线经过点B时,z最大 由可得C(a,a),此时Z=3a 由可得B(1,1),此时z=3 ∴3=4×3a ∴ 故答案: 15.(5分)给出如下四个结论: ①若“p且q”为假命题,则p、q均为假命题; ②命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”; ③若随机变量ζ~N(3,4),且P(ζ<2a﹣3)=P(ζ>a+2),则a=3; ④过点A(1,4),且横纵截距的绝对值相等的直线共有2条. 其中正确结论的序号是 ② . 【解答】解:①根据复合命题真值表,“p且q”为假命题,命题P、q至少有一个是假命题,∴①错误; ②根据否命题的定义,②正确; ③根据正态分布,μ=3取得峰值,当a=3时,2a﹣3=3,a+2=5,∴P(ξ<3)≠P(ξ>5).∴③错误; ④过点A(1,4),且横纵截距的绝对值相等的直线有x+y=5;+=1;y=4x三条直线,故④错误. 故答案是②. 三、解答题:本大题共共6小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤 16.(12分)已知函数的图象过点M(,0). (1)求m的值; (2)在△ABC中,角A,B,C的对边分别是a,b,c,若ccosB+bcosC=2acosB,求f(A)的取值范围. 【解答】解:(1)∵sinxcosx=sin2x,cos2x=(1+cos2x) ∴=sin2x﹣(1+cos2x)+m =sin2x﹣cos2x﹣+m=sin(2x﹣)﹣+m ∵函数y=fx)图象过点M(,0), ∴sin(2•﹣)﹣+m=0,解之得m= (2)∵ccosB+bcosC=2acosB, ∴结合正弦定理,得sinCcosB+cosCsinB=2sinAcosB ∵B+C=π﹣A,得sinCcosB+cosCsinB=sin(B+C)=sin(π﹣A)=sinA ∴sinA=2sinAcosB ∵△ABC中,sinA>0,∴cosB=,得B= 由(1),得f(x)=sin(2x﹣), 所以f(A)=sin(2A﹣),其中A∈(0,) ∵﹣<2A﹣<, ∴sin(2A﹣)>sin(﹣)=﹣,sin(2A﹣)≤sin=1 因此f(A)的取值范围是(﹣,1] 17.(12分)已知函数f(x)=ex+tx(e为自然对数的底数). (Ⅰ)当t=﹣e时,求函数f(x)的单调区间; (Ⅱ)若对于任意x∈(0,2],不等式f(x)>0恒成立,求实数t的取值范围. 【解答】解:(Ⅰ)当t=﹣e时,f(x)=ex﹣ex,f'(x)=ex﹣e. 由f'(x)=ex﹣e>0,解得x>1;f'(x)=ex﹣e<0,解得x<1. ∴函数f(x)的单调递增区间是(1,+∞);单调递减区间是(﹣∞,1). (Ⅱ)依题意:对于任意x∈(0,2],不等式f(x)>0恒成立, 即ex+tx>0恒成立,即在x∈(0,2]上恒成立. 令,∴. 当0<x<1时,g'(x)>0;当1<x<2时,g'(x)<0. ∴函数g(x)在(0,1)上单调递增;在(1,2)上单调递减. 所以函数g(x)在x=1处取得极大值g(1)=﹣e,即为在x∈(0,2]上的最大值. ∴实数t的取值范围是(﹣e,+∞). 所以对于任意x∈(0,2],不等式f(x)>0恒成立的实数t的取值范围是(﹣e,+∞). 18.(12分)如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点. (Ⅰ)求证:AF⊥平面CDE; (Ⅱ)求面ACD和面BCE所成锐二面角的大小. 【解答】(Ⅰ)证明:∵DE⊥平面ACD,AF⊂平面ACD,∴DE⊥AF. 又∵AC=AD,F为CD的中点,∴AF⊥CD. 又∵CD∩DE=D,AF⊥平面CDE. (Ⅱ)由(Ⅰ)可知:平面ACD⊥平面CDE. 取CE的中点Q,连接FQ,∴FQ∥DE, ∴FQ⊥平面ACD.于是可得FD,FQ,FA两两垂直,以F为坐标原点,建立如图所示的空间直角坐标系. 则F(0,0,0),C(﹣1,0,0),A,B,E(1,2,0). ∴,, 设平面BCE的法向量,则,化为, 令x=1,则y=﹣1,z=0,∴, ∵FQ⊥平面ACD,于是可取平面ACD的法向量为. ∴===. ∴平面ACD和平面BCE所成锐二面角为45°. 19.(12分)某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响. (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望; (Ⅱ)试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力. 【解答】解:(Ⅰ)设考生甲、乙正确完成实验操作的题数分别为ξ、η,则ξ=1、2、3,η=0、1、2、3. P(ξ=1)==,P(ξ=2)==,P(ξ=3)==. 所以考生甲正确完成实验操作的题数的概率分布列为: ∴Eξ==2. ∵η~B,所以考生甲正确完成实验操作的题数的概率分布列为: ξ 1 2 3 P P(η=k)=(k=0,1,2,3), ∴Eη=3×=2. (Ⅱ)∵P(ξ≥2)==,P(η≥2)=. ∴P(ξ≥2)>P(η≥2), 从做对题的数学期望上甲乙两人水平相当;从至少完成两题的概率上看,甲通过的可能性比较大,因此可以判断甲的实验操作能力强. 20.(13分)已知F(1,0),P是平面上一动点,P到直线l:x=﹣1上的射影为点N,且满足 (Ⅰ)求点P的轨迹C的方程; (Ⅱ)过点M(1,2)作曲线C的两条弦MA,MB,设MA,MB所在直线的斜率分别为k1,k2,当k1,k2变化且满足k1+k2=﹣1时,证明直线AB恒过定点,并求出该定点坐标. 【解答】解:(Ⅰ)设曲线C上任意一点P(x,y),又F(1,0),N(﹣1,y), 从而,, 则=, 由,得, 即. 化简得y2=4x,即为所求的P点的轨迹C的对应的方程. (Ⅱ)设A(x1,y1)、B(x2,y2), MA:y=k1(x﹣1)+2, MB:y=k2(x﹣1)+2. 将y=k1(x﹣1)+2与y2=4x联立,得: 由,得① 同理 ② 而AB直线方程为:, 即③ 由①②:y1+y2= 代入③得,, 整理得k1k2(x+y+1)+6+y=0. 则,故直线AB经过定点(5,﹣6). 21.(14分)已知数列{an}满足:(其中常数λ> 0,n∈N*). (Ⅰ)求数列{an}的通项公式; (Ⅱ)求证:当λ=4时,数列{an}中的任何三项都不可能成等比数列; (Ⅲ)设Sn为数列{an}的前n项和.求证:若任意n∈N*,(1﹣λ)Sn+λan≥3. 【解答】(Ⅰ)解:由①, 取n=1时,求得a1=3, 当n≥2时,有②, ①﹣②得:.∴. 又a1=3也适合上式, 所以,. (Ⅱ)证明:当λ=4时,. 下面用反证法证明 假设存在ar,as,at成等比数列, 则[(2r+1)•4r﹣1]•[(2t+1)•4t﹣1]=(2s+1)2•42s﹣2. 整理得(2r+1)(2t+1)•4r+t﹣2s=(2s+1)2. 等式右边为奇数,要使左边等于右边,则r+t﹣2s=0. 所以,(2r+1)(2t+1)=(r+t+1)2,整理得(r﹣t)2=0,∴r=t.这与r≠t矛盾, 故不存在这样的正整数r,s,t,使得ar,as,at成等比数列. (Ⅲ)证明:Sn=a1+a2+…+an =3+5λ+7λ2+…+(2n+1)λn﹣1. 当λ=1时,. 当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn﹣1③. ④. ③﹣④得: =. 所以,当λ=1时,不等式左边=(1﹣λ)Sn+λan=an=2n+1≥3,结论显然成立; 当λ≠1时,不等式左边= =. 而λ>0,1﹣λ和1﹣λn﹣1同号,故. ∴(1﹣λ)Sn+λan≥3. 综上,(1﹣λ)Sn+λan≥3对任意n∈N*都成立. 查看更多