高一数学（人教A版）必修2能力强化提升：2-2-2 平面与平面平行的判定

高一数学（人教A版）必修2能力强化提升：2-2-2 平面与平面平行的判定

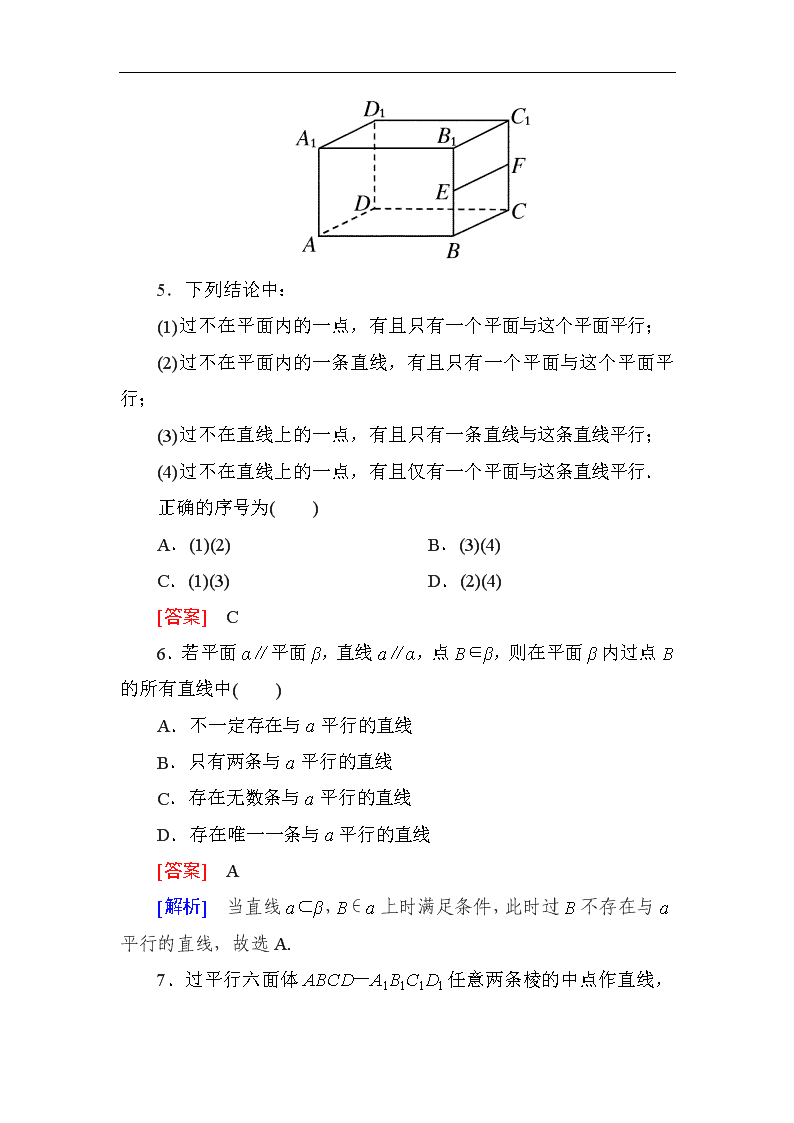
一、选择题 ‎1．如果两个平面分别经过两条平行线中的一条，那么这两个平面(　　)‎ A．平行 B．相交 C．垂直 D．都可能 ‎[答案]　D ‎[解析]　过直线的平面有无数个，考虑两个面的位置要全面．‎ ‎2．在长方体ABCD－A′B′C′D′中，下列正确的是(　　)‎ A．平面ABCD∥平面ABB′A′‎ B．平面ABCD∥平面ADD′A′‎ C．平面ABCD∥平面CDD′C′‎ D．平面ABCD∥平面A′B′C′D′‎ ‎[答案]　D ‎3．如图所示，设E，F，E1，F1分别是长方体ABCD－A1B‎1C1D1的棱AB，CD，A1B1，C1D1的中点，则平面EFD‎1A1与平面BCF1E1的位置关系是(　　)‎ A．平行 B．相交 C．异面 D．不确定 ‎[答案]　A ‎[解析]　∵E1和F1分别是A1B1和D‎1C1的中点，‎ ‎∴A1D1∥E‎1F1，又A1D1⊄平面BCF1E1，E‎1F1⊂平面BCF1E1，‎ ‎∴A1D1∥平面BCF1E1.‎ 又E1和E分别是A1B1和AB的中点，‎ ‎∴A1E1綊BE，∴四边形A1EBE1是平行四边形，‎ ‎∴A1E∥BE1，‎ 又A1E⊄平面BCF1E1，BE1⊂平面BCF1E1，‎ ‎∴A1E∥平面BCF1E1，‎ 又A1E⊂平面EFD‎1A1，A1D1⊂平面EFD‎1A1，A1E∩A1D1＝A1，‎ ‎∴平面EFD‎1A1∥平面BCF1E1.‎ ‎4．已知直线l，m，平面α，β，下列命题正确的是(　　)‎ A．l∥β，l⊂α⇒α∥β B．l∥β，m∥β，l⊂α，m⊂α⇒α∥β C．l∥m，l⊂α，m⊂β⇒α∥β D．l∥β，m∥β，l⊂α，m⊂α，l∩m＝M⇒α∥β ‎[答案]　D ‎[解析]　如图所示，在长方体ABCD－A1B‎1C1D1中，直线AB∥CD，则直线AB∥平面DC1，直线AB⊂平面AC，但是平面AC与平面DC1不平行，所以选项A错误；取BB1的中点E，CC1的中点F，则可证EF∥平面AC，B‎1C1∥平面AC.又EF⊂平面BC1，B‎1C1⊂平面BC1，但是平面AC与平面BC1不平行，所以选项B错误；直线AD∥B‎1C1，AD⊂平面AC，B‎1C1⊂平面BC1，但平面AC与平面BC1不平行，所以选项C错误；很明显选项D是两个平面平行的判定定理，所以选项D正确．‎ ‎5．下列结论中：‎ ‎(1)过不在平面内的一点，有且只有一个平面与这个平面平行；‎ ‎(2)过不在平面内的一条直线，有且只有一个平面与这个平面平行；‎ ‎(3)过不在直线上的一点，有且只有一条直线与这条直线平行；‎ ‎(4)过不在直线上的一点，有且仅有一个平面与这条直线平行．‎ 正确的序号为(　　)‎ A．(1)(2) B．(3)(4)‎ C．(1)(3) D．(2)(4)‎ ‎[答案]　C ‎6．若平面α∥平面β，直线a∥α，点B∈β，则在平面β内过点B的所有直线中(　　)‎ A．不一定存在与a平行的直线 B．只有两条与a平行的直线 C．存在无数条与a平行的直线 D．存在唯一一条与a平行的直线 ‎[答案]　A ‎[解析]　当直线a⊂β，B∈a上时满足条件，此时过B不存在与a平行的直线，故选A.‎ ‎7．过平行六面体ABCD－A1B‎1C1D1‎ 任意两条棱的中点作直线，其中与平面DBB1D1平行的直线共有(　　)‎ A．4条 B．6条 C．8条 D．12条 ‎[答案]　D ‎[解析]　如图所示，以E为例，易证EI，EQ∥平面DBB1D1.‎ 与E处于同等地位的点还有F、G、H、M、N、P、Q，故有符合题意的直线＝8条．以I为例，易证IE∥平面DBB1D1，与I处于同等地位的点还有J，K，L，故有符合题意的直线4条．∴共有8＋4＝12(条)．‎ ‎8．如图是四棱锥的平面展开图，其中四边形ABCD为正方形，E，F，G，H分别为PA，PD，PC，PB的中点，在此几何体中，给出下面四个结论：‎ ‎①平面EFGH∥平面ABCD；‎ ‎②平面PAD∥BC；‎ ‎③平面PCD∥AB；‎ ‎④平面PAD∥平面PAB.‎ 其中正确的有(　　)‎ A．①③ B．①④‎ C．①②③ D．②③‎ ‎[答案]　C ‎[解析]　把平面展开图还原为四棱锥如图所示，则EH∥AB，所以EH∥平面ABCD.同理可证EF∥平面ABCD，所以平面EFGH∥平面ABCD；平面PAD，平面PBC，平面PAB，平面PDC均是四棱锥的四个侧面，则它们两两相交．‎ ‎∵AB∥CD，‎ ‎∴平面PCD∥AB.‎ 同理平面PAD∥BC.‎ 二、填空题 ‎9．如果两个平面分别平行于第三个平面，那么这两个平面的位置关系是________．‎ ‎[答案]　平行 ‎10．已知平面α和β，在平面α内任取一条直线a，在β内总存在直线b∥a，则α与β的位置关系是________(填“平行”或“相交”)．‎ ‎[答案]　平行 ‎[解析]　假若α∩β＝l，则在平面α内，与l相交的直线a，设a∩l＝A，对于β内的任意直线b，若b过点A，则a与b相交，若b不过点A，则a与b异面，即β内不存在直线b∥a.故α∥β.‎ ‎11.‎ 如图所示，在正方体ABCD－A1B‎1C1D1中，E、F、G、H分别为棱CC1、C1D1、D1D、CD的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足________时，有MN∥平面B1BDD1.‎ ‎[答案]　点M在FH上 ‎[解析]　∵FH∥BB1，HN∥BD，FH∩HN＝H，‎ ‎∴平面FHN∥平面B1BDD1，‎ 又平面FHN∩平面EFGH＝FH，‎ ‎∴当M∈FH时，MN⊂平面FHN，‎ ‎∴MN∥平面B1BDD1.‎ ‎12．如下图是正方体的平面展开图，在这个正方体中，‎ ‎①BM∥平面DE；‎ ‎②CN∥平面AF；‎ ‎③平面BDM∥平面AFN；‎ ‎④平面BDE∥平面NCF.‎ 以上四个命题中，正确命题的序号是________．‎ ‎[答案]　①②③④‎ ‎[解析]　展开图可以折成如图a所示的正方体．‎ 在正方体中，连接AN，如图b所示．‎ ‎∵AB∥MN，且AB＝MN，‎ ‎∴四边形ABMN是平行四边形．‎ ‎∴BM∥AN.∴BM∥平面DE.同理可证CN∥平面AF，∴①②‎ 正确；‎ 如图c所示，连接NF，BE，BD，DM，可以证明BM∥平面AFN，BD∥平面AFN，则平面BDM∥平面AFN，同理可证平面BDE∥平面NCF，所以③④正确．‎ 三、解答题 ‎13．在三棱锥P－ABC中，E、F、G分别在侧棱PA、PB、PC上，且＝＝＝，求证平面EFG∥平面ABC.‎ ‎[分析]　要证平面EFG∥平面ABC，依据判定定理需在平面EFG内寻找两条相交直线分别与平面ABC平行，考虑已知条件的比例关系可产生平行线，故应从比例关系入手先找线线平行关系．‎ ‎[证明]　在△PAB中，∵＝，∴EF∥AB，‎ ‎∵EF⊄平面ABC，AB⊂平面ABC，‎ ‎∴EF∥平面ABC，同理FG∥平面ABC，‎ ‎∵EF∩FG＝F，且FG⊂平面EFG，EF⊂平面EFG，‎ ‎∴平面EFG∥平面ABC.‎ 总结评述：欲证“面面平行”，可证“线面平行”；证“线面平行”，可通过证“线线平行”来完成，这是立体几何最常用的化归与转化的思想．‎ ‎14．如图，F，H分别是正方体ABCD－A1B‎1C1D1的棱CC1，AA1的中点，求证：平面BDF∥平面B1D1H.‎ ‎[证明]　取DD1中点E，‎ 连AE、EF.‎ ‎∵E、F为DD1、CC1中点，‎ ‎∴EF綊CD.‎ ‎∴EF綊AB，‎ ‎∴四边形EFBA为平行四边形．‎ ‎∴AE∥BF.‎ 又∵E、H分别为D1D、A‎1A中点，‎ ‎∴D1E綊HA，∴四边形HAED1为平行四边形．‎ ‎∴HD1∥AE，‎ ‎∴HD1∥BF，‎ 由正方体的性质易知B1D1∥BD，且已证BF∥D1H.‎ ‎∵B1D1⊄平面BDF，BD⊂平面BDF，‎ ‎∴B1D1∥平面BDF.‎ ‎∵HD1⊄平面BDF，BF⊂平面BDF，‎ ‎∴HD1∥平面BDF.又∵B1D1∩HD1＝D1，‎ ‎∴平面BDF∥平面B1D1H.‎ ‎15．如图所示，在正方体ABCD－A1B‎1C1D1中，S是B1D1的中点，E，F，G分别是BC，DC和SC的中点，求证：‎ ‎(1)直线EG∥平面BDD1B1；‎ ‎(2)平面EFG∥平面BDD1B1.‎ ‎[证明]　(1)如图所示，连接SB.‎ ‎∵E，G分别是BC，SC的中点，‎ ‎∴EG∥SB.‎ 又∵SB⊂平面BDD1B1，EG⊄平面BDD1B1，‎ ‎∴直线EG∥平面BDD1B1.‎ ‎(2)连接SD.∵F，G分别是DC，SC的中点，∴FG∥SD.‎ 又∵SD⊂平面BDD1B1，FG⊄平面BDD1B1，‎ ‎∴FG∥平面BDD1B1.‎ 又EG∥平面BDD1B1，且EG⊂平面EFG，FG⊂平面EFG，EG∩FG＝G，‎ ‎∴平面EFG∥平面BDD1B1.‎ ‎16．如图所示，在三棱柱ABC－A1B‎1C1中，点D为AC 的中点，点D1是A‎1C1上的一点，当等于何值时，BC1∥平面AB1D1?‎ ‎[解析]　＝1.‎ 证明如下：如图所示，‎ 此时D1为线段A‎1C1的中点，连接A1B交AB1于O，连接OD1.‎ 由棱柱的定义，知四边形A1ABB1为平行四边形，‎ ‎∴点O为A1B的中点．‎ 在△A1BC1中，点O，D1分别为A1B，A‎1C1的中点，‎ ‎∴OD1∥BC1.‎ 又∵OD1⊂平面AB1D1，BC1⊄平面AB1D1，‎ ‎∴BC1∥平面AB1D1.‎ ‎∴当＝1时，BC1∥平面AB1D1.‎