- 2021-06-15 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教A版 相似三角形的判定与 性质 课时作业
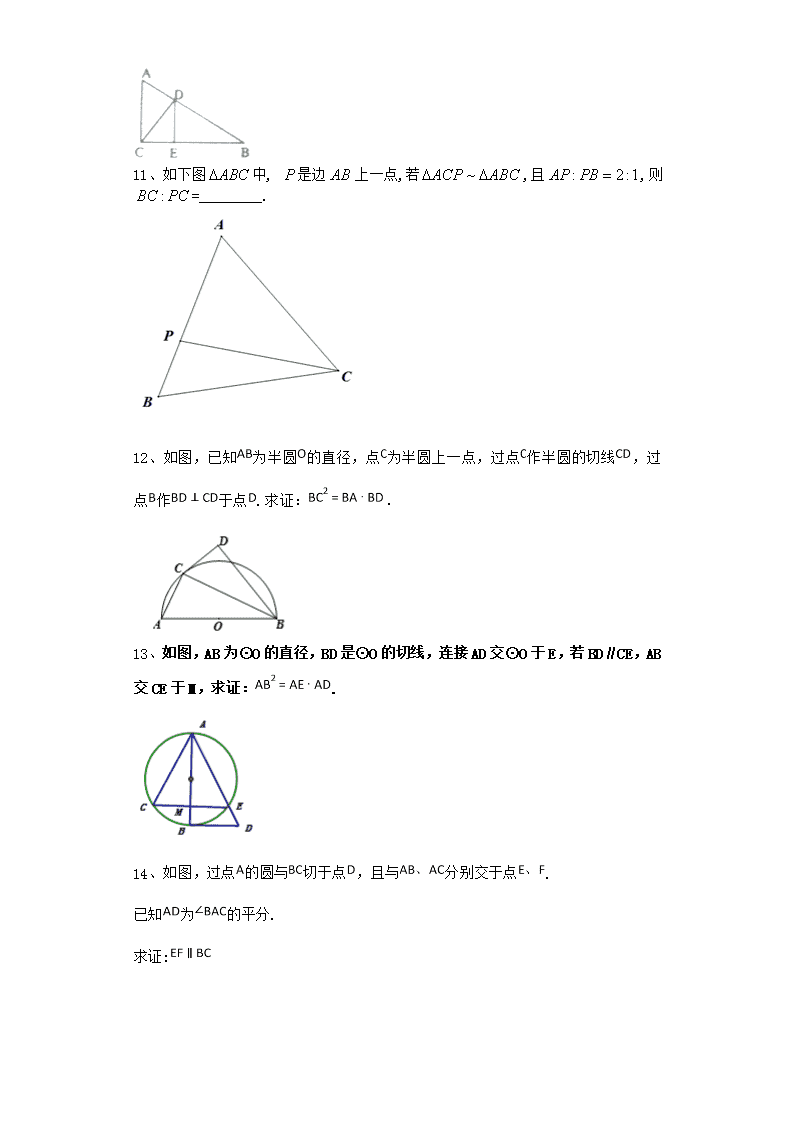
2020届一轮复习人教A版 相似三角形的判定与 性质 课时作业 1、如图,正四面体中,是棱上的动点,设(),记与所成角为,与所成角为,则( ) A. B. C.当时, D.当时, 2、正方形的边长为1,点在边上,点在边上,.动点从出发沿直线向运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点第一次碰到时,与正方形的边碰撞的次数为( ) A.4 B.3 C.8 D.6 3、如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1, l2与l3间的距离是2,正三角形ABC的三顶点分别在l1、l2、l3上,则△ABC的边长是 ( ) A. B. C. D. 4、正方体的棱长为2,点为的中点,点为线段上靠近的三等分点,平面交于点,则的长为 A. B. C. D. 5、已知圆的半径为2,圆的一条弦的长是3, 是圆上的任意一点,则的最大值为 ( ) A. 9 B. 10 C. D. 6、如图,是圆的切线,切点为点,直线与圆交于、两点,的角平分线交弦、于、两点,已知,,则的值为 . 7、如图所示的圆中,已知圆心角∠AOB=,半径OC与弦AB垂直,垂足为点D.若CD的长为,则与弦AB所围成的弓形ACB的面积为______________. 8、正方形的边长为1,分别为边上的点,若的周长为2,则__________. 9、我国古代数学著作《九章算术》中记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步有木.问邑方几何?”示意图如下图,正方形中,,分别为和的中点,若,,,,且过点,则正方形的边长为_____. 10、如图, ,垂足分别为,若,则的长为__________. 11、如下图中, 是边上一点,若,且,则=_________. 12、如图,已知为半圆的直径,点为半圆上一点,过点作半圆的切线,过点作于点.求证:. 13、如图,AB为⊙O的直径,BD是⊙O的切线,连接AD交⊙O于E,若BD∥CE,AB交CE于M,求证:. 14、如图,过点的圆与切于点,且与分别交于点. 已知为的平分. 求证: 15、在直角三角形ABC中,,它的内切圆分别与边,,相切于点,,,联结,与内切圆相交于另一点,联结,,,,已知,求证:(1);(2)。 16、已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是CB、CD上的点,且. (1)求证:四边形是梯形; (2)若,求梯形的中位线的长. 17、在△ABC中,,△ABC的外接圆⊙O的弦AD的延长线交BC的延长线于点E. 求证:△ABD∽△AEB. 18、如图,在中,是其垂心,的延长线与边和的外接圆分别交于点、,且. (1)求的大小; (2)证明:. 19、如图,点,,,在圆上,,的延长线交于点,,交于点,且.若,,求的长. 20、如图,圆的弦,交于点,且为弧的中点,点在弧上.若,求的度数. 参考答案 1、答案:D 作交于时,为正三角形,,是与成的角,根据等腰三角形的性质,作交于,同理可得,当时,,故选D. 2、答案:D 根据已知中的点E,F的位置,可知入射角的正切值为,通过相似三角形,来确定反射后的点的位置,从而可得反射的次数. 【详解】 根据已知中的点E,F的位置,可知入射角的正切值为,第一次碰撞点为F, 在反射的过程中,直线是平行的,利用平行关系及三角形的相似可得第二次碰撞点为G, G在DA上,且DG, 第三次碰撞点为H,H在DC上,且DH, 第四次碰撞点为M,M在CB上,且CM, 第五次碰撞点为N,N在DA上,且AN, 第六次回到E点,AE. 故需要碰撞6次即可. 故选:D. 名师点评: 本题主要考查了反射原理与三角形相似知识的运用.通过相似三角形,来确定反射后的点的位置,从而可得反射的次数,属于难题. 3、答案:D 【分析】 设与直线交于点.作于,于于. 设,则可得,.由可得 ,然后根据勾股定理可得,于是可得△ABC的边长为. 【详解】 设与直线交于点.作于,于于. 设,则可得,于是. 由题意得, ∴,即, 解得, ∴. 在中, 可得, ∴, ∴正△ABC的边长. 故选D. 名师点评: 本题考查相似三角形的判定与性质,平行线之间的距离,等边三角形的性质,勾股定理等,考查学生的转化能力和运算能力,在本题的解法中作辅助线将问题进行转化是关键. 4、答案:D 如图,将平移至为靠近的三个等分点处, , 为的中点, 也为中点, ,根据四点共面, , ,故选D. 5、答案:C 如图所示,连接OA,OB. 过点O作OC⊥AB,垂足为C. 则. ∴cos∠OAB= 当且仅当且同向时取等号。 ∴的最大值 故选C. 6、答案:. 由切割线定理可得,由于切圆于点,由弦切角定理可知,由于是的角平分线,则,所以, 由相似三角形得. 考点:1.切割线定理;2.相似三角形 7、答案: 根据弓形ACB的面积等于扇形OAB的面积减去△AOB的面积求解可得所求. 【详解】 设扇形的半径为,则在△OAD中,, ∴,即, 解得. ∴扇形面积为, 又, ∴. 名师点评: 解答本题的关键是将弓形的面积转化为扇形的面积与三角形面积的差,然后再根据相关公式求解,考查转化能力和计算能力. 8、答案:. 分析:本题考查了几何图形的简单应用,根据图形构建全等三角形,求得角度。 详解: 由题意,得 ,因为边长为1 所以 所以 两式相减,得 延长AB至M,使 ,连接CM,易证 所以 因为 ,所以 ,即 在 与中 所以, 所以 名师点评:本题考查了几何图形的简单应用,关键是找准各个线段间的相互关系,属于中档题。 9、答案: 利用可得的关系,从而求得即得正方形的边长. 【详解】 因为,,所以, 而,故, 所以,因为中点,所以,故, 所以=150即正方形的边长为300,填300 . 名师点评: 本题考查三角形相似,为基础题. 10、答案: ∵AC⊥BC,DE⊥BC,∴DE∥AC, ∵AC=6,DE=4,∴==, 设AD=x,则AB=3x,由射影定理可得36=x?3x, ∴x=2,∴BD=4 由射影定理可得CD==. 故答案为: . 11、答案: 由三角形的相似关系可得: , 由可得: ,则: , 据此可得: . 12、答案:证明见解析. 试题分析:【分析】 先证明,再得到. 【详解】 证明:因为为圆的切线,弧所对的圆周角为, 所以.① 又因为为半圆的直径, 所以. 又BD⊥CD,所以.② 由①②得, 所以. 名师点评: 本题主要考查相似三角形的判断和性质,意在考查学生对这些知识的掌握水平和分析推理能力. 13、答案:试题分析:连接CB,先证明∠ACB=∠ABD,所以△ACB∽△ABD,所以,即得证. 【详解】 连接CB, 因为AB为⊙O的直径,BD是⊙O的切线,所以 因为BD∥CE,所以 因为AB交CE于M,所以M为CE的中点, 所以AC=AE,。 因为BD是⊙O的切线,所以∠ABD=90° 因为AB为⊙O的直径,所以∠ACB=90°,所以∠ACB=∠ABD. 因为,所以△ACB∽△ABD,所以,所以 即 名师点评: 本题主要考查平面几何圆的知识,考查相似三角形的判定和性质,意在考查学生对这些知识的掌握水平和分析推理能力. 14、答案:试题分析:由切线的性质知,再根据角平分线的性质及平行线的判定定理求出. 证明:如图,连接. 因为圆与切于,所以. 因为平分.所以. 又,所以. 所以. 名师点评:主要考查的是相似三角形判定及有关性质的应用,切线的性质,比较简单. 15、答案:(1)见解析;(2)见解析. 试题分析:分析:(1)可证∽;(2)可证同位角或内错角相等,如证或,这又可通过证明∽证得. 详解:(1)联结,,则是等腰直角三角形,于是,故。 又,则∽,所以①. (2)由,, 知∽,∽。于是,. 故由①得,② 因,结合②得。∽,从而也是等腰三角形。于是,,所以。 名师点评:本题考查证明三角形相似,证明线段成比例或角相等,一般通过证明三角形相似,掌握相似三角形的判定定理和性质定理是解题基础. 16、答案:(1)见解析;(2) 试题分析:分析:(1)首先根据三角的中位线定理得到,且,根据三角形相似得到,且,从而,且成立,即可得结论;(2)根据梯形中位线的长度等于上底和下底之和的一半可得结果. 详解:证明:(1)在中,E、H分别是AB、AD的中点, 所以,且 在中,, 所以,且 所以四边形中,,且, 因此,四边形EFGH是梯形; (2)由(1)知, 从而,梯形的中位线的长为. 名师点评:本题考查直线与直线平行的判定,梯形中位线的长度,考查学生分析解决问题的能力,属于基础题. 17、答案:试题分析:由AB=AC,有∠ABC=∠ACB,又⊙O中,,得到∠ADB=∠ABC,即可证明△ABD∽△AEB. 试题因为, 所以. 又⊙O中,, 所以. 又, 所以△ABD∽△AEB. 18、答案:(1)(2)见解析 试题分析:(1)根据垂心的定义可得,再根据可得,因此.(2)先根据三角形相似得,再根据等角对等边得,即得结论 试题解:(1)在中,是其垂心,CE交AB于H,有, 又,所以,故. (2)由(1)知,则,即,连接,则,所以,可知,从而有. 19、答案: 试题分析:利用题意结合圆的性质和相似三角形的性质可得DF=1. 试题 因为,所以. 因为,所以. 因为,, 所以,又. 所以,故. 所以,又因为, 所以∽,则. 又因为,,所以. 20、答案:45° 试题分析:同弧或等弧所对的圆周角相等,利用等量代换,借助角与角的关系求出所求的角. 试题连结,. 因为为弧的中点,所以. 而, 所以, 即. 又因为, 所以, 故. 名师点评:平面几何选讲部分要注意与圆有关的定理,特别是涉及到角的关系的定理,寻求角的相等,边与边的关系,大多利用全等三角形或相似三角形解题. 查看更多