- 2021-06-15 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习 集合与常用逻辑用语课件(28张)(全国通用)
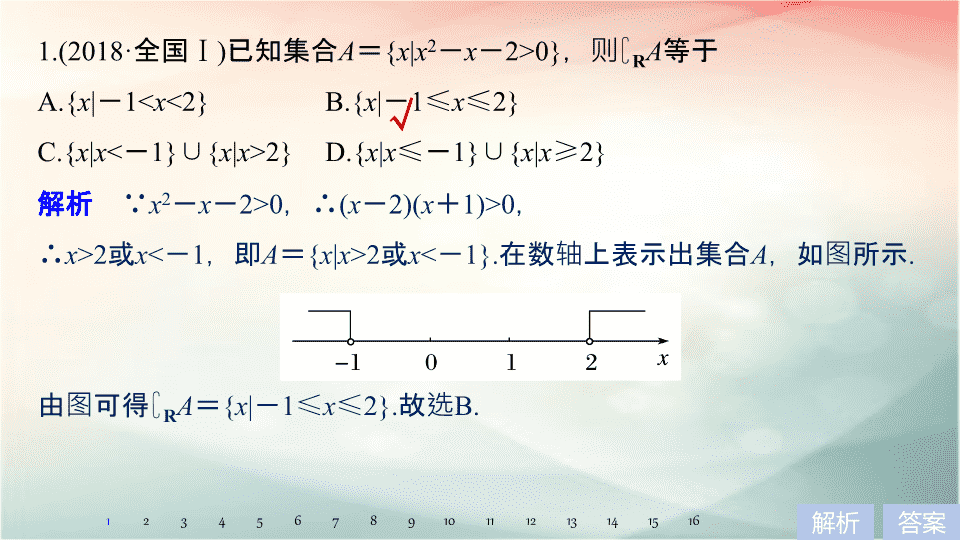
第 1 讲 集合与常用逻辑用语 板块二 练透基础送分小考点 [ 考情考向分析 ] 1. 集合是高考必考知识点,经常以不等式解集、函数的定义域、值域为背景考查集合的运算,近几年有时也会出现一些集合的新定义问题 . 2. 高考中考查命题的真假判断或命题的否定,考查充要条件的判断 . 1.(2018· 全国 Ⅰ ) 已知集合 A = { x | x 2 - x - 2>0} ,则 ∁ R A 等于 A.{ x | - 1< x <2} B .{ x | - 1 ≤ x ≤ 2} C.{ x | x < - 1} ∪ { x | x >2} D.{ x | x ≤ - 1} ∪ { x | x ≥ 2} 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 解析 解析 ∵ x 2 - x - 2>0 , ∴ ( x - 2)( x + 1)>0 , ∴ x >2 或 x < - 1 ,即 A = { x | x >2 或 x < - 1}. 在数轴上表示出集合 A ,如图所示 . 由 图可得 ∁ R A = { x | - 1 ≤ x ≤ 2 }. 故 选 B. √ 2.(2018· 安徽省江南十校联考 ) 已知集合 A = { x | y = ln(1 - 2 x )} , B = { x |e x >1} ,则 A. A ∪ B = { x | x >0} B. A ∩ B = C. A ∩ ∁ R B = D.( ∁ R A ) ∪ B = R 答案 解析 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 3. A , B , C 三个学生参加了一次考试, A , B 的得分均为 70 分, C 的得分为 65 分 . 已知命题 p :若及格分低于 70 分,则 A , B , C 都没有及格 . 在下列四个命题中,为 p 的逆否命题的是 A. 若及格分不低于 70 分,则 A , B , C 都及格 B. 若 A , B , C 都及格,则及格分不低于 70 分 C. 若 A , B , C 至少有一人及格,则及格分不低于 70 分 D. 若 A , B , C 至少有一人及格,则及格分高于 70 分 答案 解析 √ 解析 根据原命题与它的逆否命题之间的关系知,命题 p :若及格分低于 70 分,则 A , B , C 都没有及格, p 的逆否命题是:若 A , B , C 至少有 1 人及格,则及格分不低于 70 分 . 故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 4.(2018· 长春模拟 ) 设命题 p : ∀ x ∈ (0 ,+ ∞ ) , ln x ≤ x - 1 ,则 綈 p 是 A. 綈 p : ∀ x ∈ (0 ,+ ∞ ) , ln x > x - 1 B. 綈 p : ∀ x ∈ ( - ∞ , 0] , ln x > x - 1 C. 綈 p : ∃ x 0 ∈ (0 ,+ ∞ ) , ln x 0 > x 0 - 1 D. 綈 p : ∃ x 0 ∈ (0 ,+ ∞ ) , ln x 0 ≤ x 0 - 1 答案 √ 解析 解析 因为全称命题的否定是特称 ( 存在性 ) 命题, 所以命题 p : ∀ x ∈ (0 ,+ ∞ ) , ln x ≤ x - 1 的否定 綈 p 为 ∃ x 0 ∈ (0 ,+ ∞ ) , ln x 0 > x 0 - 1. 故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 6. 有关命题的说法正确的是 A. 命题 “ 若 xy = 0 ,则 x = 0 ” 的否命题为: “ 若 xy = 0 ,则 x ≠ 0 ” B. 命题 “ ∃ x 0 ∈ R ,使得 2 x - 1<0 ” 的否定是: “ ∀ x ∈ R , 2 x 2 - 1<0 ” C. “ 若 x + y = 0 ,则 x , y 互为相反数 ” 的逆命题为真命题 D. 命题 “ 若 cos x = cos y ,则 x = y ” 的逆否命题为真命题 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 对于 A 选项,命题 “ 若 xy = 0 ,则 x = 0 ” 的否命题为 “ 若 xy ≠ 0 ,则 x ≠ 0 ” ,否命题是条件和结论的双重否定,故 A 错误 ; 对于 B 选项,命题 “ ∃ x 0 ∈ R ,使 2 x - 1<0 ” 的否定是 “ ∀ x ∈ R ,2 x 2 - 1 ≥ 0 ” ,故 B 错误 ; 选项 C 的逆命题为真命题,故 C 正确 ; 选项 D 的原命题是假命题,则逆否命题与之对应也是假命题,故 D 错误,故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 7.(2018· 天津 ) 设 x ∈ R ,则 “ ” 是 “ x 3 <1 ” 的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 由 x 3 <1 ,得 x <1 , 当 x ≤ 0 时, 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 8.(2018· 山东枣庄市第三中学调研 ) 若 f ( x ) = sin(2 x + θ ) ,则 “ f ( x ) 的图象 关于 x = 对称 ” 是 “ θ = ” 的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 9 .(2018· 武汉调研 ) 给出下列两个命题 : p 1 : ∃ x 0 ∈ R , 3sin x 0 + 4cos x 0 = 3 ; p 2 :若 lg a 2 + 2lg b = 0 ,则 a + b ≥ 2 ,那么下列命题为真命题的是 A. p 1 ∧ p 2 B. p 1 ∨ ( 綈 p 2 ) C. p 1 ∨ p 2 D .( 綈 p 1 ) ∧ p 2 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 因为 3sin x + 4cos x = 5sin( x + φ ) ∈ [ - 5 , 5] , 对于 p 2 ,由题设有 a 2 b 2 = 1 , b >0 ,所以 ab = 1 或 ab =- 1 , 所以 p 1 ∨ ( 綈 p 2 ) 为真命题,故选 B. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 10.(2018· 漳州调研 ) 已知命题 p :椭圆 25 x 2 + 9 y 2 = 225 与双曲线 x 2 - 3 y 2 = 12 有相同的焦点;命题 q :函数 f ( x ) = 的 最小值 为 , 下列命题为真命题的是 A. p ∧ q B .( 綈 p ) ∧ q C. 綈 ( p ∨ q ) D. p ∧ ( 綈 q ) 答案 √ 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 所以 ( 綈 p ) ∧ q 为真命题,故选 B. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 11. 用 C ( A ) 表示非空集合 A 中的元素个数 , 定义 A * B = 若 A = {1,2} , B = { x |( x 2 + ax )( x 2 + ax + 2) = 0} ,且 A * B = 1 ,设实数 a 的所有 可能 取值 构成的集合是 S ,则 C ( S ) 等于 A.4 B.3 C.2 D.1 答案 解析 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 由 A = {1,2} ,得 C ( A ) = 2 , 由 A * B = 1 ,得 C ( B ) = 1 或 C ( B ) = 3. 由 ( x 2 + ax )( x 2 + ax + 2) = 0 , 得 x 2 + ax = 0 或 x 2 + ax + 2 = 0. 当 C ( B ) = 1 时,方程 ( x 2 + ax )( x 2 + ax + 2) = 0 只有实根 x = 0 ,这时 a = 0 ; 当 C ( B ) = 3 时,必有 a ≠ 0 ,这时 x 2 + ax = 0 有两个不相等的实根 x 1 = 0 , x 2 =- a ,方程 x 2 + ax + 2 = 0 必有两个相等的实根,且异于 x 1 = 0 , x 2 =- a . 由 Δ = a 2 - 8 = 0 ,得 a = ± 2 , 可验证均满足题意,故 S = { - 2 , 0,2 } ,故 C ( S ) = 3. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 12. 已知集合 A = { x | x >2} ,集合 B = { x | x >3} ,以下命题正确的个数是 ① ∃ x 0 ∈ A , x 0 ∉ B ; ② ∃ x 0 ∈ B , x 0 ∉ A ; ③ ∀ x ∈ A 都有 x ∈ B ; ④ ∀ x ∈ B 都有 x ∈ A . A.4 B.3 C.2 D.1 答案 解析 √ 解析 因为 A = { x | x >2} , B = { x | x >3} , 所以 B ⊆ A ,即 B 是 A 的子集, ①④ 正确, ②③ 错误,故选 C. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 13. 设全集 U = R ,函数 f ( x ) = lg(| x + 1| + a - 1)( a <1) 的定义域为 A ,集合 B = { x |cos π x = 1} ,若 ( ∁ U A ) ∩ B 恰好有两个元素,则 a 的取值集合为 _________ _ ___. 答案 解析 { a | - 2< a ≤ 0} 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 方法一 由 | x + 1| + a - 1>0 ,可得 x > - a 或 x < a - 2 , 故 ∁ U A = [ a - 2 ,- a ]. 而 B = { x | x = 2 k , k ∈ Z } ,注意到 [ a - 2 ,- a ] 关于 x =- 1 对称, 方法二 由方法一得 , ∁ U A = [ a - 2 ,- a ] , 区间长度为- a - ( a - 2) = 2 - 2 a , B = { x | x = 2 k , k ∈ Z } , 因为 ( ∁ U A ) ∩ B 恰好有两个元素, 所以 2 ≤ 2 - 2 a <6 ,所以- 2< a ≤ 0. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 14.(2018· 北京 ) 能说明 “ 若 f ( x )> f (0) 对任意的 x ∈ (0,2] 都成立,则 f ( x ) 在 [0,2] 上是增函数 ” 为假命题的一个函数是 ___________________ _ ____. 解析 答案 f ( x ) = sin x ( 答案不唯一 ) 由正弦函数图象的对称性知,当 x ∈ (0,2] 时, f ( x )> f (0) = sin 0 = 0 , 故 f ( x ) = sin x 满足条件 f ( x )> f (0) 对任意的 x ∈ (0,2] 都成立,但 f ( x ) 在 [0,2] 上不一直都是增函数 . 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 15. 设命题 p : |4 x - 3| ≤ 1 ;命题 q : x 2 - (2 a + 1) x + a ( a + 1) ≤ 0 ,若 綈 p 是 綈 q 的必要不充分条件,则实数 a 的取值范围是 ______________. 解析 答案 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 q : x 2 - (2 a + 1) x + a ( a + 1) ≤ 0 , ∴ a ≤ x ≤ a + 1. ∵ 綈 p 是 綈 q 的必要不充分条件, ∴ q 是 p 的必要不充分条件, 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 16. 若 X 是一个集合, τ 是一个以 X 的某些子集为元素的集合,且满足: ① X 属于 τ , ∅ 属于 τ ; ② τ 中任意多个元素的并集属于 τ ; ③ τ 中任意多个元素的交集属于 τ ,则称 τ 是集合 X 上的一个拓扑 . 已知集合 X = { a , b , c } ,对于下面给出的四个集合 τ : ① τ = { ∅ , { a } , { c } , { a , b , c }} ; ② τ = { ∅ , { b } , { c } , { b , c } , { a , b , c }} ; ③ τ = { ∅ , { a } , { a , b } , { a , c }} ; ④ τ = { ∅ , { a , c } , { b , c } , { c } , { a , b , c }}. 其中是集合 X 上的一个拓扑的集合 τ 是 ______.( 填序号 ) 解析 答案 ②④ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 ① τ = { ∅ , { a } , { c } , { a , b , c }} ,但是 { a } ∪ { c } = { a , c } ∉ τ ,所以 ① 错; ②④ 都满足集合 X 上的一个拓扑集合 τ 的三个条件 . 所以 ②④ 正确 ; ③ { a , b } ∪ { a , c } = { a , b , c } ∉ τ ,所以 ③ 错 . 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 本课结束查看更多